
Question Number 29164 by abdo imad last updated on 04/Feb/18
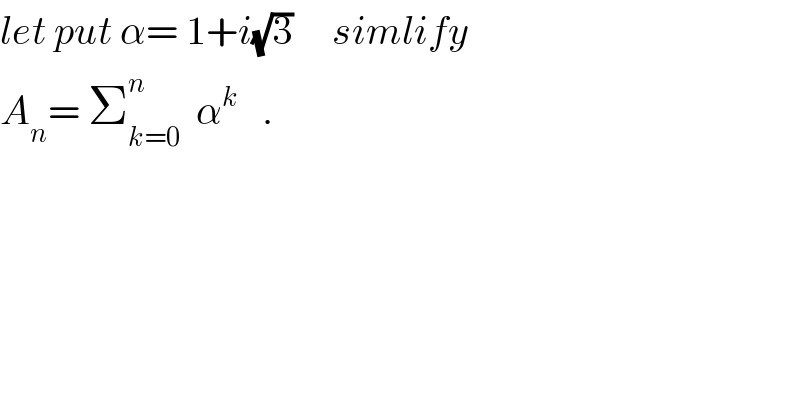
$${let}\:{put}\:\alpha=\:\mathrm{1}+{i}\sqrt{\mathrm{3}}\:\:\:\:\:{simlify} \\ $$$${A}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\alpha^{{k}} \:\:\:. \\ $$
Commented by abdo imad last updated on 06/Feb/18
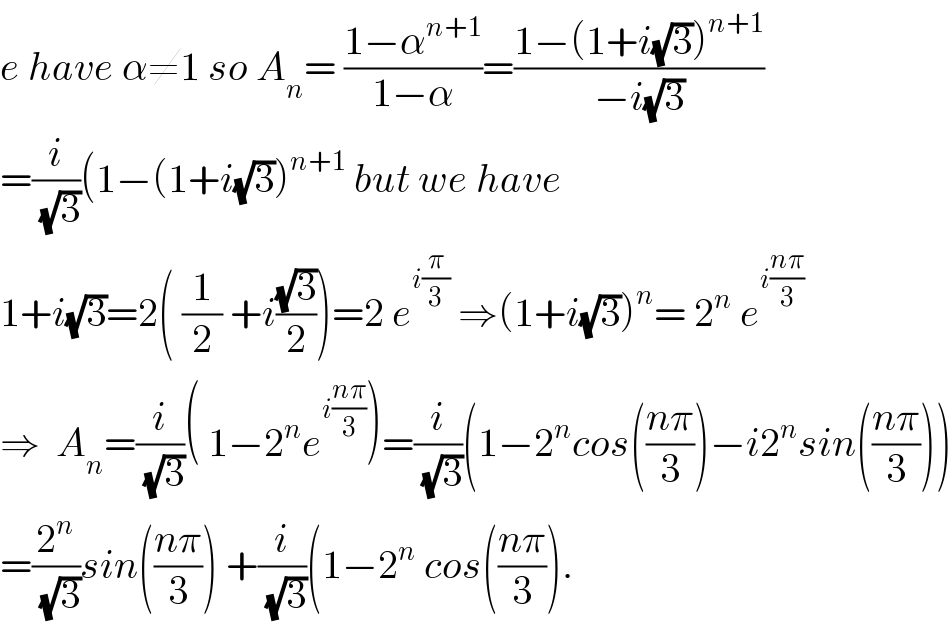
$${e}\:{have}\:\alpha\neq\mathrm{1}\:{so}\:{A}_{{n}} =\:\frac{\mathrm{1}−\alpha^{{n}+\mathrm{1}} }{\mathrm{1}−\alpha}=\frac{\mathrm{1}−\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} }{−{i}\sqrt{\mathrm{3}}}\:\: \\ $$$$=\frac{{i}}{\sqrt{\mathrm{3}}}\left(\mathrm{1}−\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} \:{but}\:{we}\:{have}\right. \\ $$$$\mathrm{1}+{i}\sqrt{\mathrm{3}}=\mathrm{2}\left(\:\frac{\mathrm{1}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\mathrm{2}\:{e}^{{i}\frac{\pi}{\mathrm{3}}} \:\Rightarrow\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)^{{n}} =\:\mathrm{2}^{{n}} \:{e}^{{i}\frac{{n}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\:\:{A}_{{n}} =\frac{{i}}{\sqrt{\mathrm{3}}}\left(\:\mathrm{1}−\mathrm{2}^{{n}} {e}^{{i}\frac{{n}\pi}{\mathrm{3}}} \right)=\frac{{i}}{\sqrt{\mathrm{3}}}\left(\mathrm{1}−\mathrm{2}^{{n}} {cos}\left(\frac{{n}\pi}{\mathrm{3}}\right)−{i}\mathrm{2}^{{n}} {sin}\left(\frac{{n}\pi}{\mathrm{3}}\right)\right) \\ $$$$=\frac{\mathrm{2}^{{n}} }{\sqrt{\mathrm{3}}}{sin}\left(\frac{{n}\pi}{\mathrm{3}}\right)\:+\frac{{i}}{\sqrt{\mathrm{3}}}\left(\mathrm{1}−\mathrm{2}^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{3}}\right).\right. \\ $$
