Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 29846 by abdo imad last updated on 12/Feb/18

give the developpement at integr series for f(x)=((ln(1+x)−ln(1−x))/x) 2)find lim_(x→0) f(x).

$${give}\:{the}\:{developpement}\:\:{at}\:{integr}\:{series}\:{for} \\ $$$${f}\left({x}\right)=\frac{{ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)}{{x}} \\ $$$$\left.\mathrm{2}\right){find}\:\:\:{lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right). \\ $$

Commented by maxmathsup by imad last updated on 09/Apr/19

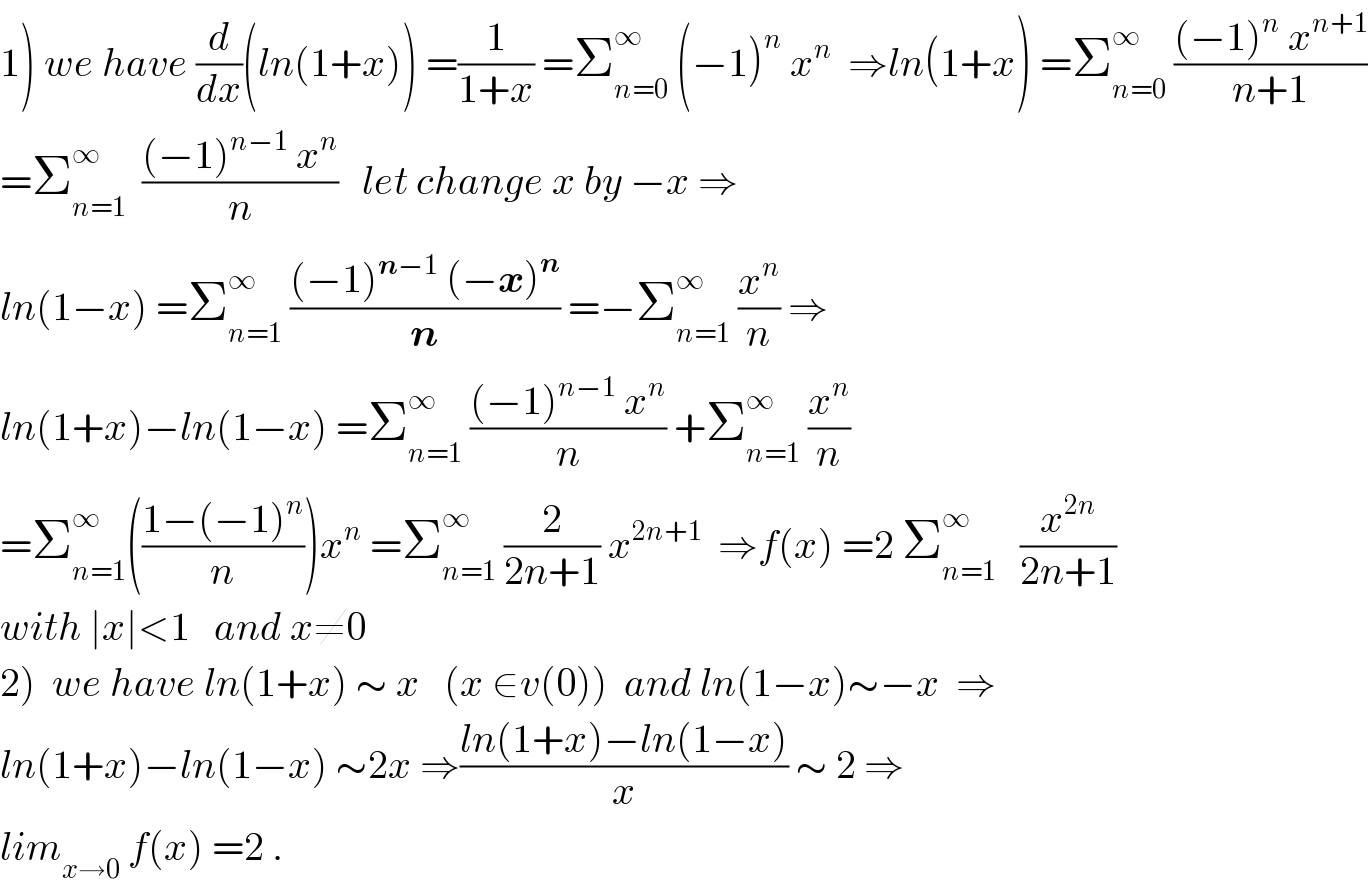
1) we have (d/dx)(ln(1+x)) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x) =Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) let change x by −x ⇒ ln(1−x) =Σ_(n=1) ^∞ (((−1)^(n−1) (−x)^n )/n) =−Σ_(n=1) ^∞ (x^n /n) ⇒ ln(1+x)−ln(1−x) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) +Σ_(n=1) ^∞ (x^n /n) =Σ_(n=1) ^∞ (((1−(−1)^n )/n))x^n =Σ_(n=1) ^∞ (2/(2n+1)) x^(2n+1) ⇒f(x) =2 Σ_(n=1) ^∞ (x^(2n) /(2n+1)) with ∣x∣<1 and x≠0 2) we have ln(1+x) ∼ x (x ∈v(0)) and ln(1−x)∼−x ⇒ ln(1+x)−ln(1−x) ∼2x ⇒((ln(1+x)−ln(1−x))/x) ∼ 2 ⇒ lim_(x→0) f(x) =2 .

$$\left.\mathrm{1}\right)\:{we}\:{have}\:\frac{{d}}{{dx}}\left({ln}\left(\mathrm{1}+{x}\right)\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:\:\Rightarrow{ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{{n}} }{{n}}\:\:\:{let}\:{change}\:{x}\:{by}\:−{x}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}−\mathrm{1}} \:\left(−\boldsymbol{{x}}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{{n}} }{{n}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} }{{n}}\right){x}^{{n}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:\Rightarrow{f}\left({x}\right)\:=\mathrm{2}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$${with}\:\mid{x}\mid<\mathrm{1}\:\:\:{and}\:{x}\neq\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:\:{we}\:{have}\:{ln}\left(\mathrm{1}+{x}\right)\:\sim\:{x}\:\:\:\left({x}\:\in{v}\left(\mathrm{0}\right)\right)\:\:{and}\:{ln}\left(\mathrm{1}−{x}\right)\sim−{x}\:\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)\:\sim\mathrm{2}{x}\:\Rightarrow\frac{{ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)}{{x}}\:\sim\:\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right)\:=\mathrm{2}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com