
Question Number 29849 by abdo imad last updated on 12/Feb/18
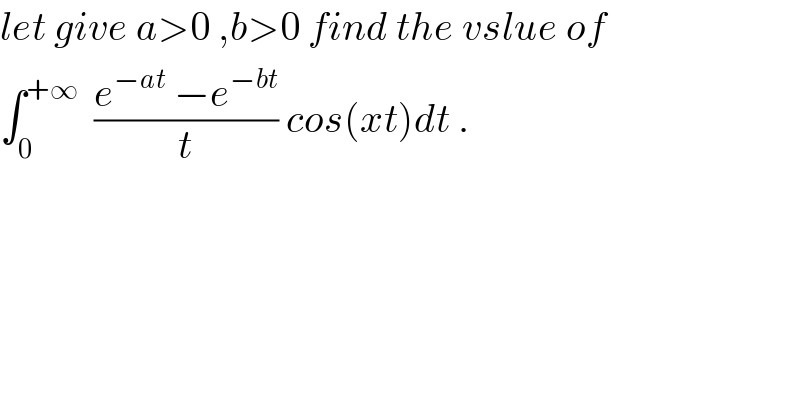
$${let}\:{give}\:{a}>\mathrm{0}\:,{b}>\mathrm{0}\:{find}\:{the}\:{vslue}\:{of}\: \\ $$ $$\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{e}^{−{at}} \:−{e}^{−{bt}} }{{t}}\:{cos}\left({xt}\right){dt}\:. \\ $$
Commented byabdo imad last updated on 19/Feb/18
![let put F(x)= ∫_0 ^∞ ((e^(−at) −e^(−bt) )/t)cos(xt)dt after verifying tbat F is derivable we have F^′ (x)= ∫_0 ^∞ (∂/∂x)( ((e^(−at) −e^(−bt) )/t)cos(xt))dt =−∫_0 ^∞ (e^(−at) − e^(−bt) )sin(xt)dt=Im(∫_0 ^∞ (e^(−bt) −e^(−at) )e^(ixt) dt) =Im( ∫_0 ^∞ e^((−b+ix)t) −e^((−a+ix)t) )dt but ∫_0 ^∞ e^((−b+ix)t) dt= (1/(−b+ix)) [ e^((−b+ix)t) ]_(t=0) ^∞ = ((−1)/(−b +ix)) = (1/(b−ix)) also we have ∫_0 ^∞ e^((−a+ix)t) dt= (1/(a−ix)) ⇒ (dF/dx)(x)= (1/(b−ix)) −(1/(a−ix))= ((b+ix)/(b^2 +x^2 )) − ((a+ix)/(a^2 +x^2 )) =(b/(b^2 +x^2 )) −(a/(a^2 +x^2 )) +ix( (1/(b^2 +x^2 )) − (1/(a^2 +x^2 )))⇒ (dF/dx)(x)=x ((a^2 +x^2 −b^2 −x^2 )/((a^2 +x^2 )(b^2 +x^2 )))=(((a^2 −b^2 )x)/((a^2 +x^2 )(b^2 +x^2 )))⇒ F(x)= ∫ (x/(b^2 +x^2 ))dx −∫ (x/(a^2 +x^2 ))dx +λ =(1/2)ln(b^2 +x^2 ) −(1/2)ln(a^2 +x^2 ) +λ F(x)=(1/2)ln(((x^2 +b^2 )/(x^2 +a^2 ))) +λ λ=lim_(x→0) (F(x)−(1/2)ln( ((x^2 +b^2 )/(x^2 +a^2 ))))=F(o)−ln((b/a)) λ=∫_0 ^∞ ((e^(−at) −e^(−bt) )/t)dt −ln((b/a)) let put I(ξ)=∫_ξ ^(+∞) ((e^(−at) −e^(−bt) )/t)dt=∫_ξ ^∞ (e^(−at) /t)dt −∫_ξ ^∞ (e^(−bt) /t)dt ch.at=u give ∫_ξ ^∞ (e^(−at) /t)dt= ∫_(aξ) ^(+∞) (e^(−u) /(u/a)) (du/a)= ∫_(aξ) ^(+∞) (e^(−u) /u)du⇒ I(ξ)= ∫_(aξ) ^(+∞) (e^(−u) /u)du −∫_(bξ) ^(+∞) (e^(−u) /u)du=∫_(aξ) ^(bξ) (e^(−u) /u) du but ∃ c_ ∈]aξ,bξ[ / I(ξ)= e^(−ξ) ∫_(aξ) ^(bξ) (du/u)=e^(−ξ) ln((b/a)) ⇒ ∫_0 ^∞ ((e^(−at) −e^(−bt) )/t)dt=lim_(ξ→0) I(ξ)=ln((b/a)) ⇒ λ=0 and F(x)=(1/2)ln(((x^2 +b^2 )/(x^2 +a^2 ))) .](Q30242.png)
$${let}\:{put}\:{F}\left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{at}} \:−{e}^{−{bt}} }{{t}}{cos}\left({xt}\right){dt}\:{after}\:{verifying}\:{tbat} \\ $$ $${F}\:{is}\:{derivable}\:{we}\:{have} \\ $$ $${F}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\frac{\partial}{\partial{x}}\left(\:\frac{{e}^{−{at}} \:−{e}^{−{bt}} }{{t}}{cos}\left({xt}\right)\right){dt} \\ $$ $$=−\int_{\mathrm{0}} ^{\infty} \:\left({e}^{−{at}} \:−\:{e}^{−{bt}} \right){sin}\left({xt}\right){dt}={Im}\left(\int_{\mathrm{0}} ^{\infty} \left({e}^{−{bt}} \:−{e}^{−{at}} \right){e}^{{ixt}} {dt}\right) \\ $$ $$={Im}\left(\:\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{b}+{ix}\right){t}} \:−{e}^{\left(−{a}+{ix}\right){t}} \right){dt}\:{but} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−{b}+{ix}\right){t}} {dt}=\:\frac{\mathrm{1}}{−{b}+{ix}}\:\left[\:{e}^{\left(−\boldsymbol{{b}}+\boldsymbol{{ix}}\right)\boldsymbol{{t}}} \right]_{\boldsymbol{{t}}=\mathrm{0}} ^{\infty} =\:\frac{−\mathrm{1}}{−{b}\:+{ix}}\:=\:\frac{\mathrm{1}}{{b}−{ix}} \\ $$ $${also}\:{we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{a}+{ix}\right){t}} {dt}=\:\frac{\mathrm{1}}{{a}−{ix}}\:\Rightarrow \\ $$ $$\frac{{dF}}{{dx}}\left({x}\right)=\:\frac{\mathrm{1}}{{b}−{ix}}\:−\frac{\mathrm{1}}{{a}−{ix}}=\:\frac{{b}+{ix}}{{b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:−\:\frac{{a}+{ix}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} } \\ $$ $$=\frac{{b}}{{b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:−\frac{{a}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:\:+{ix}\left(\:\frac{\mathrm{1}}{{b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\right)\Rightarrow \\ $$ $$\frac{{dF}}{{dx}}\left({x}\right)={x}\:\frac{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \:−{x}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){x}}{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}\Rightarrow \\ $$ $${F}\left({x}\right)=\:\int\:\:\:\frac{{x}}{{b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }{dx}\:−\int\:\frac{{x}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }{dx}\:+\lambda \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({b}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)\:+\lambda \\ $$ $${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right)\:+\lambda \\ $$ $$\lambda={lim}_{{x}\rightarrow\mathrm{0}} \left({F}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\:\frac{{x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right)\right)={F}\left({o}\right)−{ln}\left(\frac{{b}}{{a}}\right) \\ $$ $$\lambda=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{at}} \:−{e}^{−{bt}} }{{t}}{dt}\:−{ln}\left(\frac{{b}}{{a}}\right)\:{let}\:{put} \\ $$ $${I}\left(\xi\right)=\int_{\xi} ^{+\infty} \:\:\:\frac{{e}^{−{at}} \:−{e}^{−{bt}} }{{t}}{dt}=\int_{\xi} ^{\infty} \:\:\frac{{e}^{−{at}} }{{t}}{dt}\:−\int_{\xi} ^{\infty} \:\frac{{e}^{−{bt}} }{{t}}{dt}\:{ch}.{at}={u} \\ $$ $${give}\:\int_{\xi} ^{\infty} \:\:\frac{{e}^{−{at}} }{{t}}{dt}=\:\int_{{a}\xi} ^{+\infty} \:\:\frac{{e}^{−{u}} }{\frac{{u}}{{a}}}\:\frac{{du}}{{a}}=\:\int_{{a}\xi} ^{+\infty} \:\frac{{e}^{−{u}} }{{u}}{du}\Rightarrow \\ $$ $${I}\left(\xi\right)=\:\int_{{a}\xi} ^{+\infty} \:\frac{{e}^{−{u}} }{{u}}{du}\:−\int_{{b}\xi} ^{+\infty} \:\:\frac{{e}^{−{u}} }{{u}}{du}=\int_{{a}\xi} ^{{b}\xi} \:\:\frac{{e}^{−{u}} }{{u}}\:{du}\:{but} \\ $$ $$\left.\exists\:{c}_{} \in\right]{a}\xi,{b}\xi\left[\:/\:\:{I}\left(\xi\right)=\:{e}^{−\xi} \:\int_{{a}\xi} ^{{b}\xi} \:\frac{{du}}{{u}}={e}^{−\xi} {ln}\left(\frac{{b}}{{a}}\right)\:\Rightarrow\right. \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{at}} \:−{e}^{−{bt}} }{{t}}{dt}={lim}_{\xi\rightarrow\mathrm{0}} \:{I}\left(\xi\right)={ln}\left(\frac{{b}}{{a}}\right)\:\Rightarrow\:\lambda=\mathrm{0}\:{and} \\ $$ $${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right)\:\:. \\ $$
