
Previous in Relation and Functions Next in Relation and Functions
Question Number 29973 by abdo imad last updated on 14/Feb/18
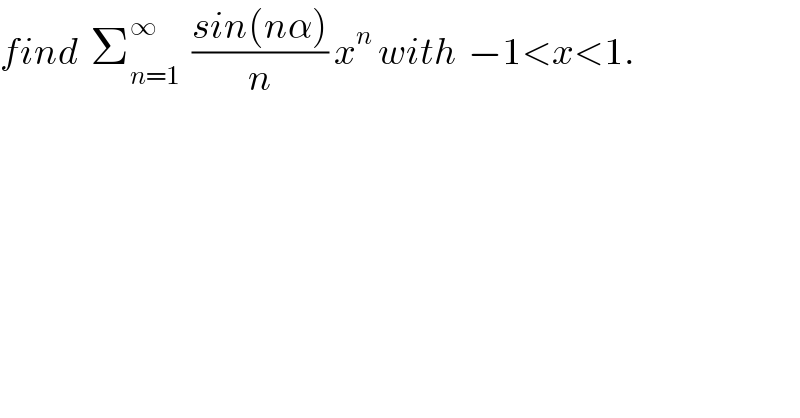
$${find}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{sin}\left({n}\alpha\right)}{{n}}\:{x}^{{n}} \:{with}\:\:−\mathrm{1}<{x}<\mathrm{1}. \\ $$
Commented byabdo imad last updated on 16/Feb/18
![let put S(x)=Σ_(n=1) ^∞ ((sin(nα))/n)x^n due to uniform convergence we have S^′ (x)=Σ_(n=1) ^∞ sin(nα)x^(n−1) =Σ_(n=0) ^∞ sin((n+1)α)x^n =Im( Σ_(n=0) ^∞ e^(i(n+1)α) x^n )=Im( e^(iα) Σ_(n=0) ^∞ ( x e^(iα) )^n ) we have ∣x e^(iα) ∣<1⇒ e^(iα) Σ_(n=0) ^∞ (xe^(iα) )^n = e^(iα) (1/(1−xe^(iα) )) = (1/(e^(−iα) −x)) =(1/(cosα −i sinα −x)) =(1/(cosα−x −isinα)) = ((cosα −x +i sinα)/((cosα−x)^2 +sin^2 α)) ⇒Im(Σ(...))= ((sinα)/((x−cosα)^2 +sin^2 α))⇒ S(x)=∫_0 ^x ((sinα)/((t−cosα)^2 +sin^2 α))dt +λ but λ=S(0)=0 the ch . t−cosα =sinα u give S(x) =∫_(−cotanα) ^((x−cosα)/(sinα)) ((sinα)/(sin^2 u^2 +sin^2 α)) sinαdu = ∫_(−cotanα) ^(((x−cosα)/(sinα)) ) (du/(1+u^2 )) = [ arctanu]_(−cotanα) ^((x−cosα)/(sinα)) = artan(((x−cosα)/(sinα))) +artan(cotanα) .](Q30107.png)
$${let}\:{put}\:{S}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({n}\alpha\right)}{{n}}{x}^{{n}} \:{due}\:{to}\:{uniform}\:{convergence} \\ $$ $${we}\:{have}\:{S}^{'} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:{sin}\left({n}\alpha\right){x}^{{n}−\mathrm{1}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:{sin}\left(\left({n}+\mathrm{1}\right)\alpha\right){x}^{{n}} \\ $$ $$={Im}\left(\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{e}^{{i}\left({n}+\mathrm{1}\right)\alpha} \:{x}^{{n}} \right)={Im}\left(\:{e}^{{i}\alpha} \:\sum_{{n}=\mathrm{0}} ^{\infty} \left(\:{x}\:{e}^{{i}\alpha} \right)^{{n}} \right)\:{we}\:{have} \\ $$ $$\mid{x}\:{e}^{{i}\alpha} \mid<\mathrm{1}\Rightarrow\:{e}^{{i}\alpha} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({xe}^{{i}\alpha} \right)^{{n}} \:=\:{e}^{{i}\alpha} \:\frac{\mathrm{1}}{\mathrm{1}−{xe}^{{i}\alpha} }\:=\:\frac{\mathrm{1}}{{e}^{−{i}\alpha} \:−{x}} \\ $$ $$\:=\frac{\mathrm{1}}{{cos}\alpha\:−{i}\:{sin}\alpha\:−{x}}\:\:=\frac{\mathrm{1}}{{cos}\alpha−{x}\:−{isin}\alpha} \\ $$ $$=\:\:\frac{{cos}\alpha\:−{x}\:+{i}\:{sin}\alpha}{\left({cos}\alpha−{x}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \alpha}\:\Rightarrow{Im}\left(\Sigma\left(...\right)\right)=\:\:\frac{{sin}\alpha}{\left({x}−{cos}\alpha\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \alpha}\Rightarrow \\ $$ $${S}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\:\:\:\:\:\frac{{sin}\alpha}{\left({t}−{cos}\alpha\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \alpha}{dt}\:+\lambda\:{but}\:\lambda={S}\left(\mathrm{0}\right)=\mathrm{0} \\ $$ $${the}\:{ch}\:.\:{t}−{cos}\alpha\:={sin}\alpha\:{u}\:{give} \\ $$ $${S}\left({x}\right)\:=\int_{−{cotan}\alpha} ^{\frac{{x}−{cos}\alpha}{{sin}\alpha}} \:\:\:\:\:\:\:\:\frac{{sin}\alpha}{{sin}^{\mathrm{2}} {u}^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \alpha}\:{sin}\alpha{du} \\ $$ $$=\:\int_{−{cotan}\alpha} ^{\frac{{x}−{cos}\alpha}{{sin}\alpha}\:\:} \:\:\:\:\:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\:=\:\left[\:{arctanu}\right]_{−{cotan}\alpha} ^{\frac{{x}−{cos}\alpha}{{sin}\alpha}} \\ $$ $$=\:{artan}\left(\frac{{x}−{cos}\alpha}{{sin}\alpha}\right)\:+{artan}\left({cotan}\alpha\right)\:. \\ $$
