Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

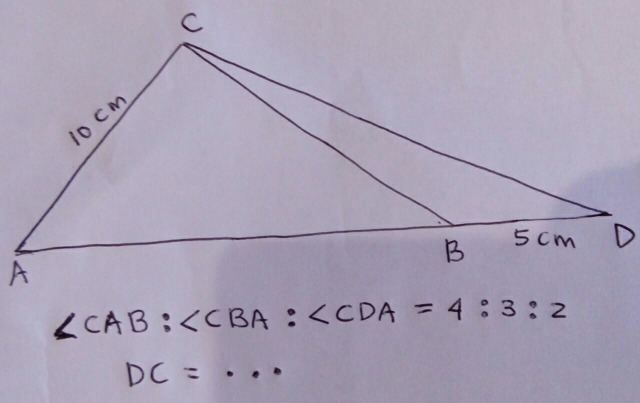
Question Number 30159 by naka3546 last updated on 17/Feb/18

Commented by mrW2 last updated on 18/Feb/18

sir, please check your question. I think the given configuration leads to no normal solution. If BD=5 cm, then AC must be between 7.5 and 9 cm to make a solution possible. E.g. if you set AC=8 cm, you′ll get DC=((40)/3) cm.

$${sir},\:{please}\:{check}\:{your}\:{question}. \\ $$$${I}\:{think}\:{the}\:{given}\:{configuration}\:{leads} \\ $$$${to}\:{no}\:{normal}\:{solution}. \\ $$$${If}\:{BD}=\mathrm{5}\:{cm},\:{then}\:{AC}\:{must}\:{be}\:{between} \\ $$$$\mathrm{7}.\mathrm{5}\:{and}\:\mathrm{9}\:{cm}\:{to}\:{make}\:{a}\:{solution} \\ $$$${possible}.\:{E}.{g}.\:{if}\:{you}\:{set}\:{AC}=\mathrm{8}\:{cm}, \\ $$$${you}'{ll}\:{get}\:{DC}=\frac{\mathrm{40}}{\mathrm{3}}\:{cm}. \\ $$

Answered by mrW2 last updated on 18/Feb/18

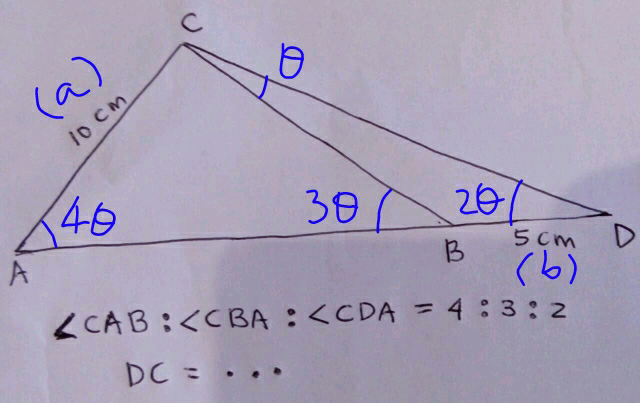
Commented by mrW2 last updated on 18/Feb/18

let λ=(a/b) (a/(sin 3θ))=((CB)/(sin 4θ)) ...(i) (b/(sin θ))=((CB)/(sin 2θ)) ...(ii) (i)/(ii): (a/(sin 3θ))×((sin θ)/b)=((sin 2θ)/(sin 4θ))=(1/(2 cos 2θ)) ⇒((λ sin θ)/(sin 3θ))=(1/(2 cos 2θ)) 2λ sin θ cos 2θ=sin 3θ=sin θ cos 2θ+cos θ sin 2θ (2λ−1) sin θ cos 2θ=cos θ sin 2θ (2λ−1) tan θ=tan 2θ=((2 tan θ)/(1−tan^2 θ)) 2λ−1=(2/(1−tan^2 θ)) tan^2 θ=1−(2/(2λ−1))>0 ⇒λ>(3/2) ⇒tan θ=(√(1−(2/(2λ−1)))) 3θ+4θ<180° ⇒θ<((180°)/7)≈2 tan^2 θ=1−(2/(2λ−1))<tan^2 (((180°)/7)) ⇒λ<(1/2)+(1/(1−tan^2 ((180°)/7)))=1.8 i.e. to make a solution possible, 1.5<λ=(a/b)<1.8 for b=5 cm: a>1.5×5=7.5 cm a<1.8×5=9 cm let′s say b=8 cm, ⇒λ=(8/5)=1.6 ⇒tan θ=(√(1−(2/(2×1.6−1))))=(1/(√(11))) ⇒θ=16.8° ⇒cos 2θ=2 cos^2 θ−1=(2/(1+tan^2 θ))−1 ⇒cos 2θ=(2/(1+(1/(11))))−1=((2×11)/(12))−1=(5/6) ((DC)/(sin 4θ))=(a/(sin 2θ)) ⇒DC=((a sin 4θ)/(sin 2θ))=2a cos 2θ=2×8×(5/6)=((40)/3)

$${let}\:\lambda=\frac{{a}}{{b}} \\ $$$$\frac{{a}}{\mathrm{sin}\:\mathrm{3}\theta}=\frac{{CB}}{\mathrm{sin}\:\mathrm{4}\theta}\:\:\:...\left({i}\right) \\ $$$$\frac{{b}}{\mathrm{sin}\:\theta}=\frac{{CB}}{\mathrm{sin}\:\mathrm{2}\theta}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\frac{{a}}{\mathrm{sin}\:\mathrm{3}\theta}×\frac{\mathrm{sin}\:\theta}{{b}}=\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\mathrm{4}\theta}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$\Rightarrow\frac{\lambda\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\mathrm{3}\theta}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$\mathrm{2}\lambda\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\mathrm{2}\theta=\mathrm{sin}\:\mathrm{3}\theta=\mathrm{sin}\:\theta\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}\:\theta\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\left(\mathrm{2}\lambda−\mathrm{1}\right)\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\mathrm{2}\theta=\mathrm{cos}\:\theta\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\left(\mathrm{2}\lambda−\mathrm{1}\right)\:\mathrm{tan}\:\theta=\mathrm{tan}\:\mathrm{2}\theta=\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{2}\lambda−\mathrm{1}=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}\lambda−\mathrm{1}}>\mathrm{0}\:\Rightarrow\lambda>\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\sqrt{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}\lambda−\mathrm{1}}} \\ $$$$\mathrm{3}\theta+\mathrm{4}\theta<\mathrm{180}° \\ $$$$\Rightarrow\theta<\frac{\mathrm{180}°}{\mathrm{7}}\approx\mathrm{2} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}\lambda−\mathrm{1}}<\mathrm{tan}^{\mathrm{2}} \:\left(\frac{\mathrm{180}°}{\mathrm{7}}\right) \\ $$$$\Rightarrow\lambda<\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\mathrm{180}°}{\mathrm{7}}}=\mathrm{1}.\mathrm{8} \\ $$$${i}.{e}.\:{to}\:{make}\:{a}\:{solution}\:{possible}, \\ $$$$\mathrm{1}.\mathrm{5}<\lambda=\frac{{a}}{{b}}<\mathrm{1}.\mathrm{8} \\ $$$${for}\:{b}=\mathrm{5}\:{cm}: \\ $$$${a}>\mathrm{1}.\mathrm{5}×\mathrm{5}=\mathrm{7}.\mathrm{5}\:{cm} \\ $$$${a}<\mathrm{1}.\mathrm{8}×\mathrm{5}=\mathrm{9}\:{cm} \\ $$$$ \\ $$$${let}'{s}\:{say}\:{b}=\mathrm{8}\:{cm},\:\Rightarrow\lambda=\frac{\mathrm{8}}{\mathrm{5}}=\mathrm{1}.\mathrm{6} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\sqrt{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}×\mathrm{1}.\mathrm{6}−\mathrm{1}}}=\frac{\mathrm{1}}{\sqrt{\mathrm{11}}}\:\Rightarrow\theta=\mathrm{16}.\mathrm{8}° \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\theta=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{2}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{11}}}−\mathrm{1}=\frac{\mathrm{2}×\mathrm{11}}{\mathrm{12}}−\mathrm{1}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\frac{{DC}}{\mathrm{sin}\:\mathrm{4}\theta}=\frac{{a}}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow{DC}=\frac{{a}\:\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{sin}\:\mathrm{2}\theta}=\mathrm{2}{a}\:\mathrm{cos}\:\mathrm{2}\theta=\mathrm{2}×\mathrm{8}×\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{40}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com