
Question Number 30299 by ajfour last updated on 19/Feb/18
Commented by ajfour last updated on 19/Feb/18

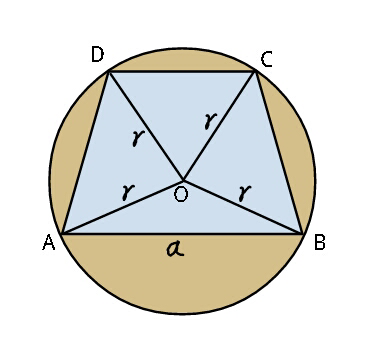
$${Find}\:{maximum}\:{area}\:{of}\: \\ $$$${quadrilateral}\:{ABCD}\:{given}\:\boldsymbol{{a}},\:\boldsymbol{{r}}\:. \\ $$
Commented by ajfour last updated on 20/Feb/18
Commented by ajfour last updated on 20/Feb/18
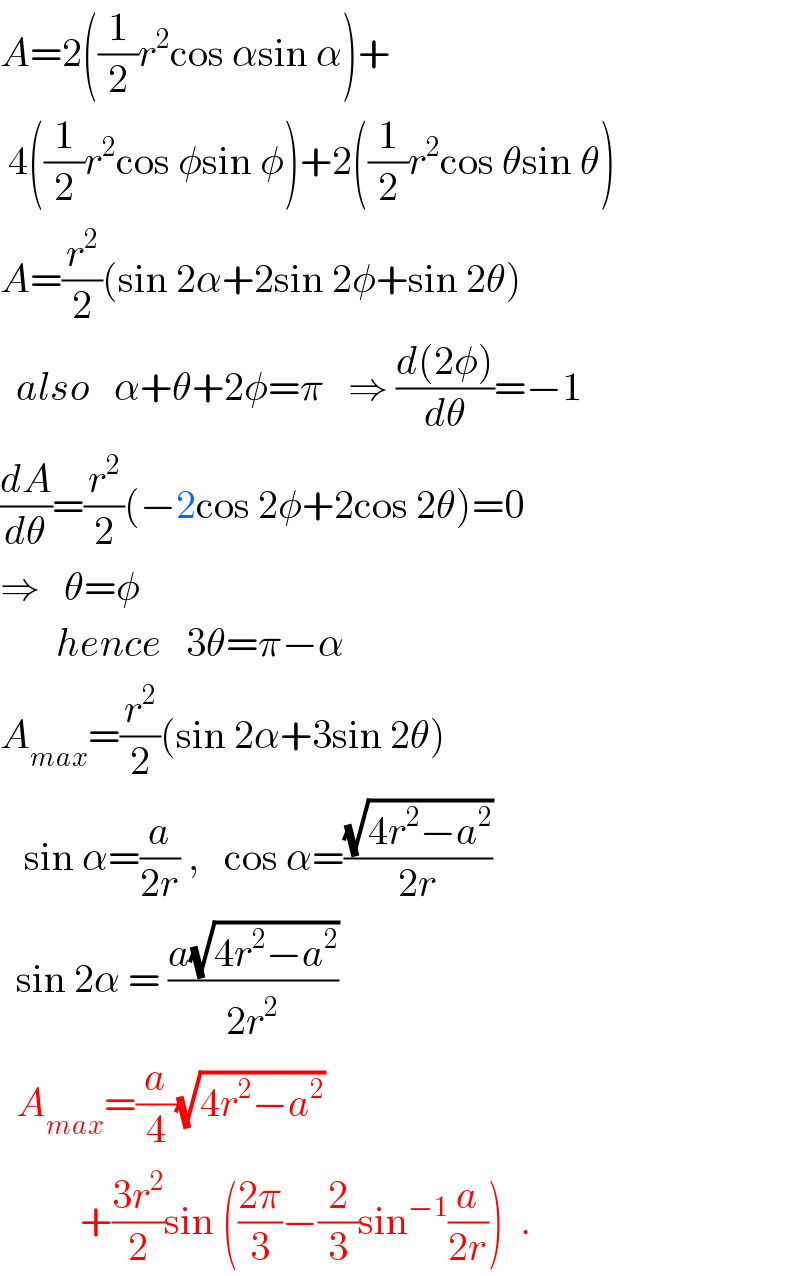
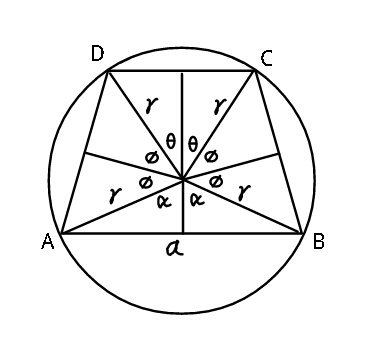
$${A}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \mathrm{cos}\:\alpha\mathrm{sin}\:\alpha\right)+ \\ $$$$\:\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \mathrm{cos}\:\phi\mathrm{sin}\:\phi\right)+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \mathrm{cos}\:\theta\mathrm{sin}\:\theta\right) \\ $$$${A}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{2sin}\:\mathrm{2}\phi+\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\:\:{also}\:\:\:\alpha+\theta+\mathrm{2}\phi=\pi\:\:\:\Rightarrow\:\frac{{d}\left(\mathrm{2}\phi\right)}{{d}\theta}=−\mathrm{1} \\ $$$$\frac{{dA}}{{d}\theta}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(−\mathrm{2cos}\:\mathrm{2}\phi+\mathrm{2cos}\:\mathrm{2}\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\theta=\phi\:\:\:\: \\ $$$$\:\:\:\:\:\:\:{hence}\:\:\:\mathrm{3}\theta=\pi−\alpha \\ $$$${A}_{{max}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{3sin}\:\mathrm{2}\theta\right) \\ $$$$\:\:\:\mathrm{sin}\:\alpha=\frac{{a}}{\mathrm{2}{r}}\:,\:\:\:\mathrm{cos}\:\alpha=\frac{\sqrt{\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}{r}} \\ $$$$\:\:\mathrm{sin}\:\mathrm{2}\alpha\:=\:\frac{{a}\sqrt{\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}{r}^{\mathrm{2}} } \\ $$$$\:\:{A}_{{max}} =\frac{{a}}{\mathrm{4}}\sqrt{\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)\:\:. \\ $$
Commented by ajfour last updated on 20/Feb/18

$${I}\:{have}\:{assumed},\:{without}\:{proof} \\ $$$${that}\:{quadrilateral}\:{shall}\:{be}\:{an} \\ $$$${isosceles}\:{trapezium}. \\ $$
Commented by mrW2 last updated on 20/Feb/18
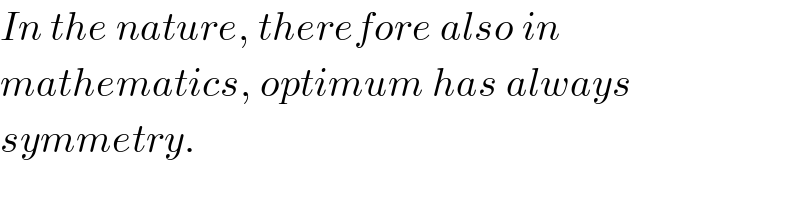
$${In}\:{the}\:{nature},\:{therefore}\:{also}\:{in}\: \\ $$$${mathematics},\:{optimum}\:{has}\:{always} \\ $$$${symmetry}. \\ $$
Answered by mrW2 last updated on 19/Feb/18
Commented by mrW2 last updated on 19/Feb/18
![sin (θ/2)=(a/(2r)) ⇒θ=2 sin^(−1) (a/(2r))=constant sin θ=2×(a/(2r))×(√(1−(a^2 /(4r^2 ))))=(a/r)(√(1−(a^2 /(4r^2 )))) α+β+γ=ϕ=2π−θ=constant A_1 =A_(AOBCD) =(r^2 /2)(sin α+sin β+sin γ) =(r^2 /2)[sin α+sin β+sin (ϕ−α−β)] (∂A_1 /∂α)=(r^2 /2)[cos α−cos (ϕ−α−β)]=0 ⇒cos α=cos (ϕ−α−β)=cos γ ⇒α=γ (∂A_1 /∂β)=(r^2 /2)[cos β−cos (ϕ−α−β)]=0 ⇒cos β=cos (ϕ−α−β)=cos γ ⇒α=β=γ=(ϕ/3)=(1/3)(2π−2 sin^(−1) (a/(2r)))=((2π)/3)−(2/3)sin^(−1) (a/(2r)) sin α=sin β=sin γ=(1/2)[(√3) cos ((2/3)sin^(−1) (a/(2r)))+sin ((2/3)sin^(−1) (a/(2r)))] max. A_(ABCD) =(r^2 /2){3sin α+sin θ} =(r^2 /2){(3/2)[(√3) cos ((2/3)sin^(−1) (a/(2r)))+sin ((2/3)sin^(−1) (a/(2r)))]+(a/r)(√(1−(a^2 /(4r^2 ))))} =((3r^2 )/4){(√3) cos ((2/3)sin^(−1) (a/(2r)))+sin ((2/3)sin^(−1) (a/(2r)))+((2a)/(3r))(√(1−(a^2 /(4r^2 ))))}](Q30304.png)
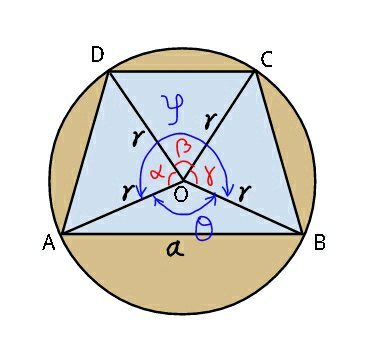
$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{a}}{\mathrm{2}{r}} \\ $$$$\Rightarrow\theta=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}={constant} \\ $$$$\mathrm{sin}\:\theta=\mathrm{2}×\frac{{a}}{\mathrm{2}{r}}×\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{r}^{\mathrm{2}} }}=\frac{{a}}{{r}}\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{r}^{\mathrm{2}} }} \\ $$$$ \\ $$$$\alpha+\beta+\gamma=\varphi=\mathrm{2}\pi−\theta={constant} \\ $$$${A}_{\mathrm{1}} ={A}_{{AOBCD}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta+\mathrm{sin}\:\gamma\right) \\ $$$$=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta+\mathrm{sin}\:\left(\varphi−\alpha−\beta\right)\right] \\ $$$$\frac{\partial{A}_{\mathrm{1}} }{\partial\alpha}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{cos}\:\alpha−\mathrm{cos}\:\left(\varphi−\alpha−\beta\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\mathrm{cos}\:\left(\varphi−\alpha−\beta\right)=\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\alpha=\gamma \\ $$$$\frac{\partial{A}_{\mathrm{1}} }{\partial\beta}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{cos}\:\beta−\mathrm{cos}\:\left(\varphi−\alpha−\beta\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\mathrm{cos}\:\left(\varphi−\alpha−\beta\right)=\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\alpha=\beta=\gamma=\frac{\varphi}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\pi−\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}} \\ $$$$\mathrm{sin}\:\alpha=\mathrm{sin}\:\beta=\mathrm{sin}\:\gamma=\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)+\mathrm{sin}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)\right] \\ $$$$ \\ $$$${max}.\:{A}_{{ABCD}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left\{\mathrm{3sin}\:\alpha+\mathrm{sin}\:\theta\right\} \\ $$$$=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left\{\frac{\mathrm{3}}{\mathrm{2}}\left[\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)+\mathrm{sin}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)\right]+\frac{{a}}{{r}}\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{r}^{\mathrm{2}} }}\right\} \\ $$$$=\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{4}}\left\{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)+\mathrm{sin}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}\right)+\frac{\mathrm{2}{a}}{\mathrm{3}{r}}\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{r}^{\mathrm{2}} }}\right\} \\ $$
Commented by ajfour last updated on 20/Feb/18
$$\:{Thank}\:{you}\:{very}\:{much}\:{Sir}. \\ $$
Commented by mrW2 last updated on 20/Feb/18

$${I}\:{saw}\:{your}\:{earlier}\:{comments},\:{but}\:{I} \\ $$$${had}\:{no}\:{time}\:{to}\:{answer}. \\ $$$${Basically}\:{one}\:{can}\:{also}\:{use}\:{only}\:{one}\:{variable} \\ $$$${to}\:{solve}\:{the}\:{question}.\:{Then}\:{we}\:{should} \\ $$$${get}\:{an}\:{eqn}.\:{like}\:\mathrm{cos}\:\left({a}−\theta\right)+\mathrm{cos}\:\mathrm{2}\theta=\mathrm{0}, \\ $$$${not}\:\mathrm{2cos}\:\left({a}−\theta\right)+\mathrm{cos}\:\mathrm{2}\theta=\mathrm{0}\:{as}\:{you}\:{got}. \\ $$$${Pls}\:{tell}\:{me}\:{more}\:{about}\:{your}\:{method}. \\ $$
Commented by ajfour last updated on 20/Feb/18

$${yes}\:{Sir},\:{you}\:{are}\:{absolutely}\:{right}, \\ $$$${i}\:{have}\:{found}\:{my}\:{error}.\:{Thank}\:{you}. \\ $$
