
Question Number 33170 by prof Abdo imad last updated on 11/Apr/18
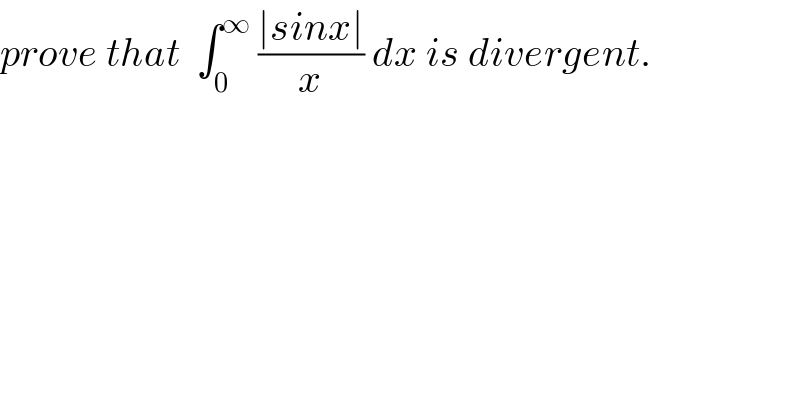
$${prove}\:{that}\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mid{sinx}\mid}{{x}}\:{dx}\:{is}\:{divergent}. \\ $$
Commented by prof Abdo imad last updated on 13/Apr/18
![∫_0 ^∞ ((∣sinx∣)/x)dx =lim_(n→+∞) A_n with A_n = ∫_0 ^(nπ) ((∣sinx∣)/x)dx but A_n = Σ_(k=0) ^n ∫_(kπ) ^((k+1)π) ((∣sinx∣)/x)dx =_(x=kπ +t) Σ_(k=0) ^n ∫_0 ^π ((sint)/(kπ +t)) dt but 0≤t≤π ⇒ kπ ≤ kπ +t ≤(k+1)π ⇒ (1/((k+1)π)) ≤ (1/(kπ+t)) ≤ (1/(kπ)) ⇒ ((sint)/(kπ+t)) ≥ ((sint)/((k+1)π)) ∀ t∈[0,π] ⇒ ∫_0 ^π ((sint)/(kπ+t)) dt ≥ (1/((k+1)π)) ∫_0 ^π sintdt = (2/((k+1)π)) ⇒ A_n ≥ (2/π) Σ_(k=0) ^n (1/(k+1)) ⇒ A_n ≥ (2/π) Σ_(k=1) ^(n+1) (1/k) ⇒ A_n ≥ (2/π) H_(n+1) _(n→+∞) →+∞ so lim_(n→+∞) A_n =+∞ and the integral is divergent.](Q33234.png)
$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mid{sinx}\mid}{{x}}{dx}\:\:={lim}_{{n}\rightarrow+\infty} \:\:{A}_{{n}} \:\:{with} \\ $$$${A}_{{n}} \:\:=\:\int_{\mathrm{0}} ^{{n}\pi} \:\:\frac{\mid{sinx}\mid}{{x}}{dx}\:\:{but}\: \\ $$$${A}_{{n}} \:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\int_{{k}\pi} ^{\left({k}+\mathrm{1}\right)\pi} \:\:\:\frac{\mid{sinx}\mid}{{x}}{dx}\:\: \\ $$$$=_{{x}={k}\pi\:+{t}} \:\:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sint}}{{k}\pi\:+{t}}\:{dt}\:\:\:{but} \\ $$$$\mathrm{0}\leqslant{t}\leqslant\pi\:\Rightarrow\:{k}\pi\:\leqslant\:{k}\pi\:+{t}\:\leqslant\left({k}+\mathrm{1}\right)\pi\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\pi}\:\leqslant\:\:\frac{\mathrm{1}}{{k}\pi+{t}}\:\leqslant\:\:\frac{\mathrm{1}}{{k}\pi}\:\Rightarrow\:\frac{{sint}}{{k}\pi+{t}}\:\geqslant\:\frac{{sint}}{\left({k}+\mathrm{1}\right)\pi}\:\:\forall\:{t}\in\left[\mathrm{0},\pi\right] \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sint}}{{k}\pi+{t}}\:{dt}\:\:\geqslant\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\pi}\:\int_{\mathrm{0}} ^{\pi} \:{sintdt}\:=\:\frac{\mathrm{2}}{\left({k}+\mathrm{1}\right)\pi}\:\Rightarrow \\ $$$${A}_{{n}} \:\:\geqslant\:\frac{\mathrm{2}}{\pi}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:\Rightarrow\:{A}_{{n}} \:\geqslant\:\frac{\mathrm{2}}{\pi}\:\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:\Rightarrow \\ $$$${A}_{{n}} \:\geqslant\:\frac{\mathrm{2}}{\pi}\:{H}_{{n}+\mathrm{1}} \:_{{n}\rightarrow+\infty} \:\rightarrow+\infty\:{so}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \:=+\infty \\ $$$${and}\:{the}\:{integral}\:{is}\:{divergent}. \\ $$
