Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 34326 by 33 last updated on 04/May/18

find the equation of the 2D curve such that the lines (x/t) + (y/((a−t) )) = 1 are always tangent to the curve. given ′a′ is a positive real constant and ′t′ is a parameter. ( 0 < t < a )

$${find}\:{the}\:{equation}\:{of}\:{the}\:\mathrm{2}{D} \\ $$ $${curve}\:{such}\:{that}\:{the}\:{lines} \\ $$ $$\:\frac{{x}}{{t}}\:+\:\frac{{y}}{\left({a}−{t}\right)\:}\:=\:\mathrm{1} \\ $$ $$\:{are}\:{always}\:{tangent}\:{to} \\ $$ $${the}\:{curve}. \\ $$ $${given}\:'{a}'\:\:{is}\:{a}\:{positive}\:{real} \\ $$ $${constant}\:{and}\:'{t}'\:{is}\:{a} \\ $$ $${parameter}.\:\left(\:\mathrm{0}\:<\:{t}\:<\:{a}\:\right) \\ $$

Answered by MJS last updated on 05/May/18

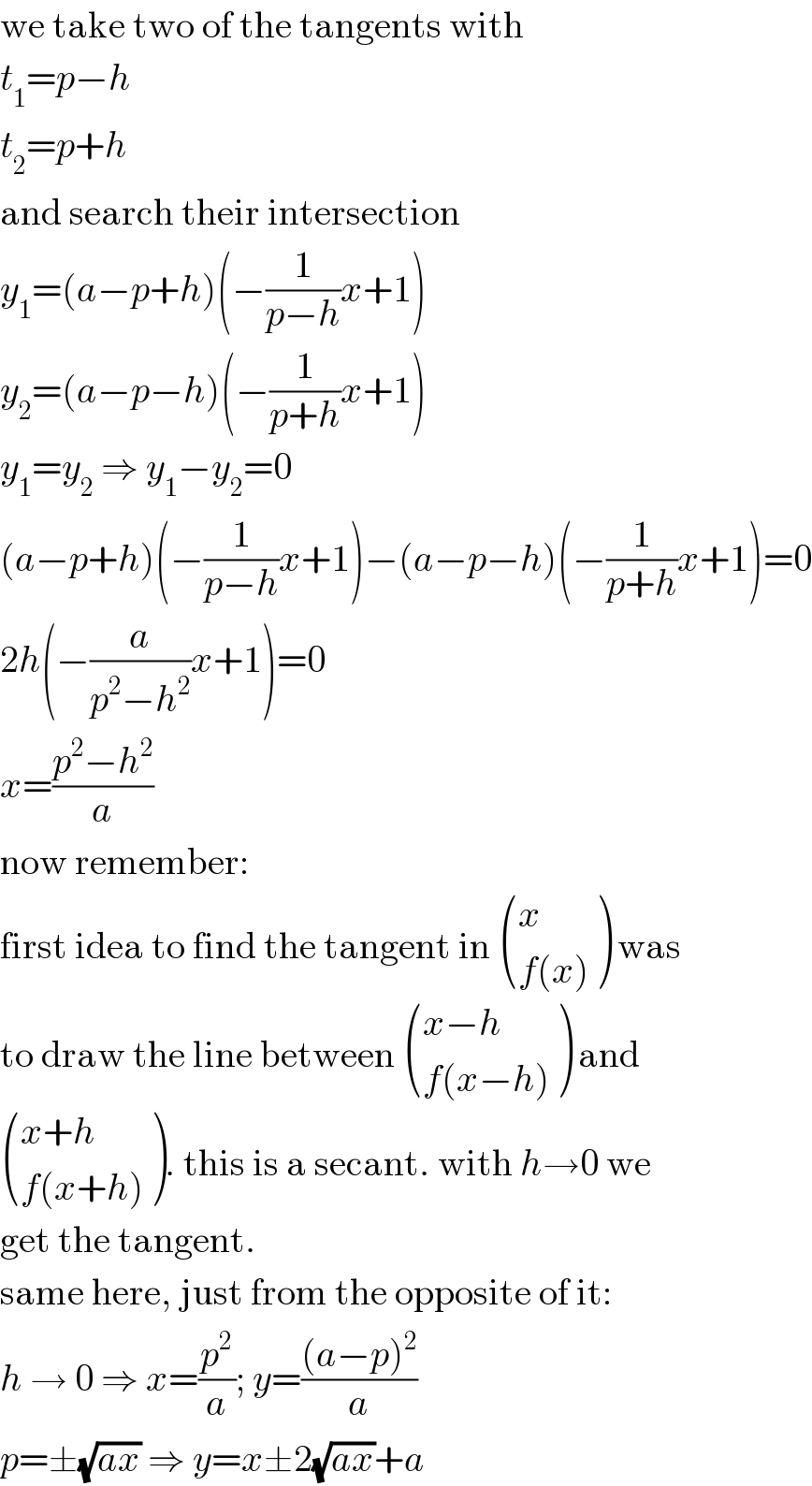
we take two of the tangents with t_1 =p−h t_2 =p+h and search their intersection y_1 =(a−p+h)(−(1/(p−h))x+1) y_2 =(a−p−h)(−(1/(p+h))x+1) y_1 =y_2 ⇒ y_1 −y_2 =0 (a−p+h)(−(1/(p−h))x+1)−(a−p−h)(−(1/(p+h))x+1)=0 2h(−(a/(p^2 −h^2 ))x+1)=0 x=((p^2 −h^2 )/a) now remember: first idea to find the tangent in ((x),((f(x))) ) was to draw the line between (((x−h)),((f(x−h))) ) and (((x+h)),((f(x+h))) ). this is a secant. with h→0 we get the tangent. same here, just from the opposite of it: h → 0 ⇒ x=(p^2 /a); y=(((a−p)^2 )/a) p=±(√(ax)) ⇒ y=x±2(√(ax))+a

$$\mathrm{we}\:\mathrm{take}\:\mathrm{two}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangents}\:\mathrm{with} \\ $$ $${t}_{\mathrm{1}} ={p}−{h} \\ $$ $${t}_{\mathrm{2}} ={p}+{h} \\ $$ $$\mathrm{and}\:\mathrm{search}\:\mathrm{their}\:\mathrm{intersection} \\ $$ $${y}_{\mathrm{1}} =\left({a}−{p}+{h}\right)\left(−\frac{\mathrm{1}}{{p}−{h}}{x}+\mathrm{1}\right) \\ $$ $${y}_{\mathrm{2}} =\left({a}−{p}−{h}\right)\left(−\frac{\mathrm{1}}{{p}+{h}}{x}+\mathrm{1}\right) \\ $$ $${y}_{\mathrm{1}} ={y}_{\mathrm{2}} \:\Rightarrow\:{y}_{\mathrm{1}} −{y}_{\mathrm{2}} =\mathrm{0} \\ $$ $$\left({a}−{p}+{h}\right)\left(−\frac{\mathrm{1}}{{p}−{h}}{x}+\mathrm{1}\right)−\left({a}−{p}−{h}\right)\left(−\frac{\mathrm{1}}{{p}+{h}}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$ $$\mathrm{2}{h}\left(−\frac{{a}}{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }{x}+\mathrm{1}\right)=\mathrm{0} \\ $$ $${x}=\frac{{p}^{\mathrm{2}} −{h}^{\mathrm{2}} }{{a}} \\ $$ $$\mathrm{now}\:\mathrm{remember}: \\ $$ $$\mathrm{first}\:\mathrm{idea}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{in}\:\begin{pmatrix}{{x}}\\{{f}\left({x}\right)}\end{pmatrix}\:\mathrm{was} \\ $$ $$\mathrm{to}\:\mathrm{draw}\:\mathrm{the}\:\mathrm{line}\:\mathrm{between}\:\begin{pmatrix}{{x}−{h}}\\{{f}\left({x}−{h}\right)}\end{pmatrix}\:\mathrm{and} \\ $$ $$\begin{pmatrix}{{x}+{h}}\\{{f}\left({x}+{h}\right)}\end{pmatrix}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{secant}.\:\mathrm{with}\:{h}\rightarrow\mathrm{0}\:\mathrm{we} \\ $$ $$\mathrm{get}\:\mathrm{the}\:\mathrm{tangent}. \\ $$ $$\mathrm{same}\:\mathrm{here},\:\mathrm{just}\:\mathrm{from}\:\mathrm{the}\:\mathrm{opposite}\:\mathrm{of}\:\mathrm{it}: \\ $$ $${h}\:\rightarrow\:\mathrm{0}\:\Rightarrow\:{x}=\frac{{p}^{\mathrm{2}} }{{a}};\:{y}=\frac{\left({a}−{p}\right)^{\mathrm{2}} }{{a}} \\ $$ $${p}=\pm\sqrt{{ax}}\:\Rightarrow\:{y}={x}\pm\mathrm{2}\sqrt{{ax}}+{a} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com