Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 34696 by abdo imad last updated on 10/May/18

let f(x) =(√(2−x)) developp f at integr serie and give the radius of convergence.

$${let}\:{f}\left({x}\right)\:=\sqrt{\mathrm{2}−{x}} \\ $$$${developp}\:{f}\:{at}\:{integr}\:{serie}\:{and}\:{give}\:{the}\:{radius}\:{of} \\ $$$${convergence}. \\ $$

Commented by math khazana by abdo last updated on 11/May/18

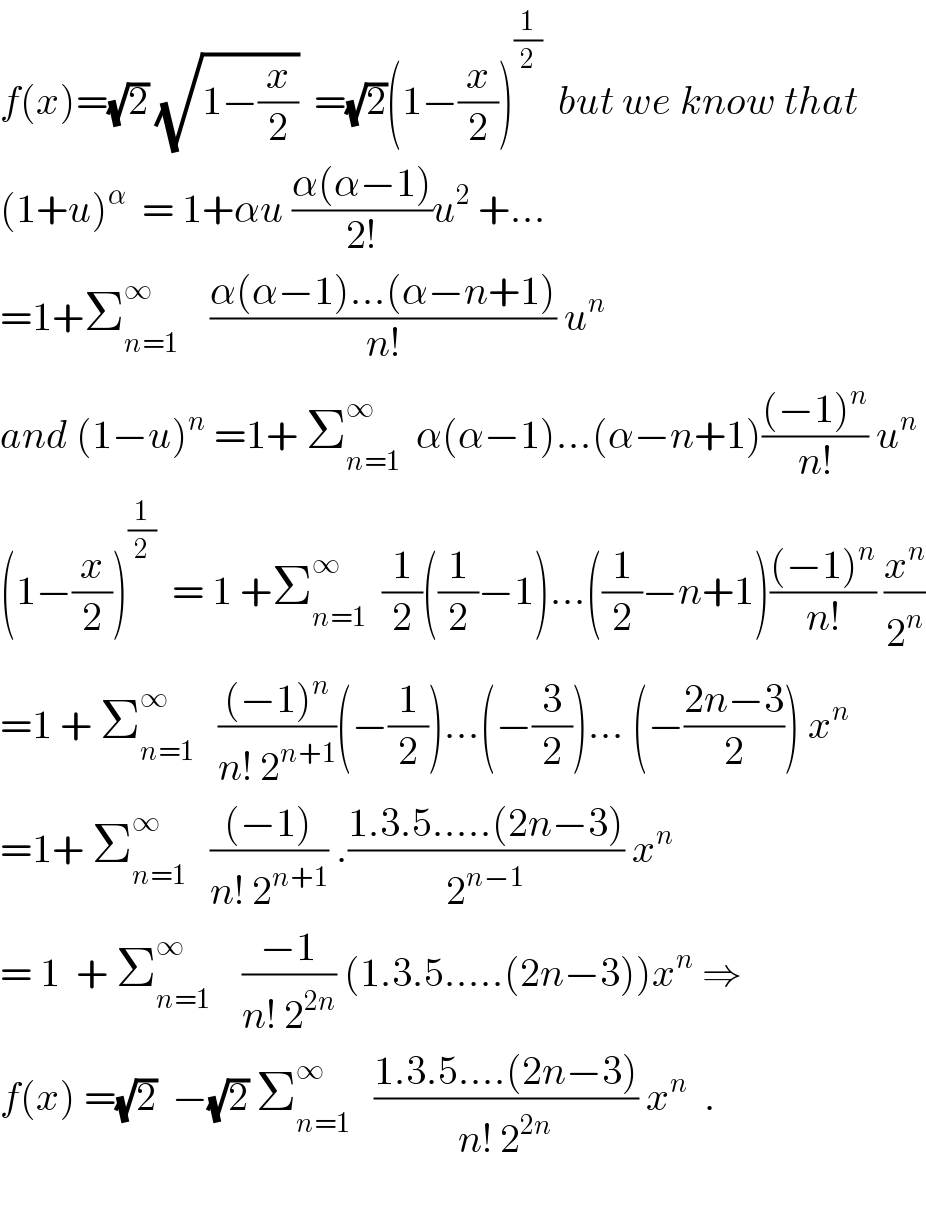
f(x)=(√2) (√(1−(x/2))) =(√2)(1−(x/2))^(1/2) but we know that (1+u)^α = 1+αu ((α(α−1))/(2!))u^2 +... =1+Σ_(n=1) ^∞ ((α(α−1)...(α−n+1))/(n!)) u^n and (1−u)^n =1+ Σ_(n=1) ^∞ α(α−1)...(α−n+1)(((−1)^n )/(n!)) u^n (1−(x/2))^(1/2) = 1 +Σ_(n=1) ^∞ (1/2)((1/2)−1)...((1/2)−n+1)(((−1)^n )/(n!)) (x^n /2^n ) =1 + Σ_(n=1) ^∞ (((−1)^n )/(n! 2^(n+1) ))(−(1/2))...(−(3/2))... (−((2n−3)/2)) x^n =1+ Σ_(n=1) ^∞ (((−1))/(n! 2^(n+1) )) .((1.3.5.....(2n−3))/2^(n−1) ) x^n = 1 + Σ_(n=1) ^∞ ((−1)/(n! 2^(2n) )) (1.3.5.....(2n−3))x^n ⇒ f(x) =(√2) −(√2) Σ_(n=1) ^∞ ((1.3.5....(2n−3))/(n! 2^(2n) )) x^n .

$${f}\left({x}\right)=\sqrt{\mathrm{2}}\:\sqrt{\mathrm{1}−\frac{{x}}{\mathrm{2}}}\:\:=\sqrt{\mathrm{2}}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:{but}\:{we}\:{know}\:{that} \\ $$$$\left(\mathrm{1}+{u}\right)^{\alpha} \:\:=\:\mathrm{1}+\alpha{u}\:\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}{u}^{\mathrm{2}} \:+... \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\alpha\left(\alpha−\mathrm{1}\right)...\left(\alpha−{n}+\mathrm{1}\right)}{{n}!}\:{u}^{{n}} \:\:\: \\ $$$${and}\:\left(\mathrm{1}−{u}\right)^{{n}} \:=\mathrm{1}+\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\alpha\left(\alpha−\mathrm{1}\right)...\left(\alpha−{n}+\mathrm{1}\right)\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:{u}^{{n}} \\ $$$$\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:=\:\mathrm{1}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)...\left(\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:\frac{{x}^{{n}} }{\mathrm{2}^{{n}} } \\ $$$$=\mathrm{1}\:+\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\:\mathrm{2}^{{n}+\mathrm{1}} }\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)...\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)...\:\left(−\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}}\right)\:{x}^{{n}} \\ $$$$=\mathrm{1}+\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)}{{n}!\:\mathrm{2}^{{n}+\mathrm{1}} }\:.\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}.....\left(\mathrm{2}{n}−\mathrm{3}\right)}{\mathrm{2}^{{n}−\mathrm{1}} }\:{x}^{{n}} \\ $$$$=\:\mathrm{1}\:\:+\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{−\mathrm{1}}{{n}!\:\mathrm{2}^{\mathrm{2}{n}} }\:\left(\mathrm{1}.\mathrm{3}.\mathrm{5}.....\left(\mathrm{2}{n}−\mathrm{3}\right)\right){x}^{{n}} \:\Rightarrow \\ $$$${f}\left({x}\right)\:=\sqrt{\mathrm{2}}\:\:−\sqrt{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}....\left(\mathrm{2}{n}−\mathrm{3}\right)}{{n}!\:\mathrm{2}^{\mathrm{2}{n}} }\:{x}^{{n}} \:\:. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com