Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 3566 by Yozzii last updated on 15/Dec/15

Let A= ((a,b),(c,d) ). Find a condition on a,b,c,d so that A^(n+1) −A^n =nA, n∈N. A^(n+1) −A^n =nA A^n −A^(n−1) =(n−1)A A^(n−1) −A^(n−2) =(n−2)A A^(n−2) −A^(n−3) =(n−3)A ... A^4 −A^3 =3A A^3 −A^2 =2A A^2 −A=A So, A^(n+1) −A=(n+n−1+n−2+...+3+2+1)A A^(n+1) =A+((n(n+1))/2)A A^(n+1) =((n^2 +n+2)/2)A A^n =(((n−1)^2 +n+1)/2)A A^n =((n^2 −n+2)/2)A (n≥1), A= ((a,b),(c,d) ) .

$${Let}\:{A}=\begin{pmatrix}{{a}}&{{b}}\\{{c}}&{{d}}\end{pmatrix}.\:{Find}\:{a}\:{condition}\:{on} \\ $$$${a},{b},{c},{d}\:{so}\:{that}\:{A}^{{n}+\mathrm{1}} −{A}^{{n}} ={nA},\:{n}\in\mathbb{N}. \\ $$$$ \\ $$$${A}^{{n}+\mathrm{1}} −{A}^{{n}} ={nA} \\ $$$${A}^{{n}} −{A}^{{n}−\mathrm{1}} =\left({n}−\mathrm{1}\right){A} \\ $$$${A}^{{n}−\mathrm{1}} −{A}^{{n}−\mathrm{2}} =\left({n}−\mathrm{2}\right){A} \\ $$$${A}^{{n}−\mathrm{2}} −{A}^{{n}−\mathrm{3}} =\left({n}−\mathrm{3}\right){A} \\ $$$$... \\ $$$${A}^{\mathrm{4}} −{A}^{\mathrm{3}} =\mathrm{3}{A} \\ $$$${A}^{\mathrm{3}} −{A}^{\mathrm{2}} =\mathrm{2}{A} \\ $$$${A}^{\mathrm{2}} −{A}={A} \\ $$$$ \\ $$$$\:{So},\:{A}^{{n}+\mathrm{1}} −{A}=\left({n}+{n}−\mathrm{1}+{n}−\mathrm{2}+...+\mathrm{3}+\mathrm{2}+\mathrm{1}\right){A} \\ $$$${A}^{{n}+\mathrm{1}} ={A}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{A} \\ $$$${A}^{{n}+\mathrm{1}} =\frac{{n}^{\mathrm{2}} +{n}+\mathrm{2}}{\mathrm{2}}{A} \\ $$$${A}^{{n}} =\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} +{n}+\mathrm{1}}{\mathrm{2}}{A} \\ $$$${A}^{{n}} =\frac{{n}^{\mathrm{2}} −{n}+\mathrm{2}}{\mathrm{2}}{A}\:\:\left({n}\geqslant\mathrm{1}\right),\:{A}=\begin{pmatrix}{{a}}&{{b}}\\{{c}}&{{d}}\end{pmatrix}\:. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by prakash jain last updated on 15/Dec/15

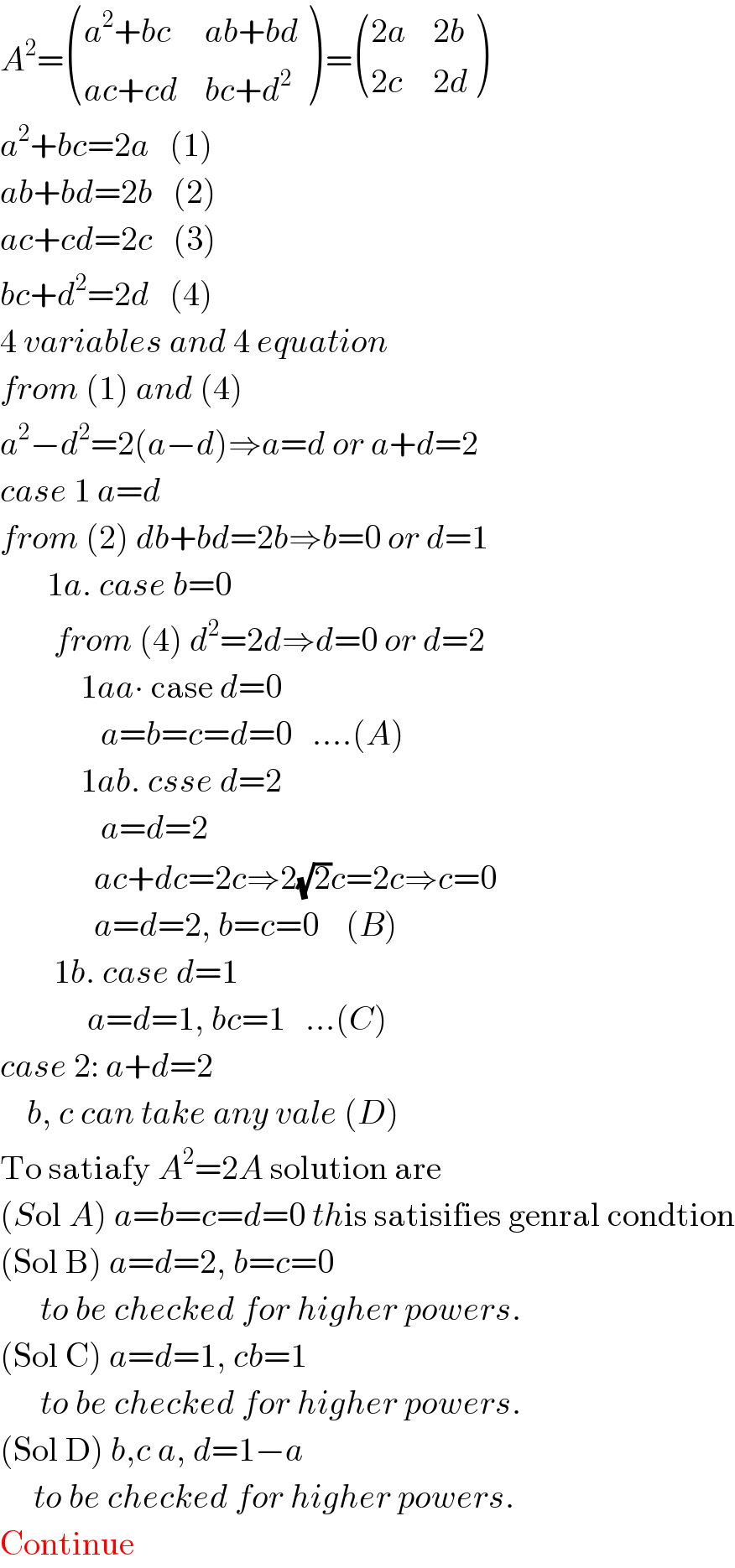
A^2 = (((a^2 +bc),(ab+bd)),((ac+cd),(bc+d^2 )) ) = (((2a),(2b)),((2c),(2d)) ) a^2 +bc=2a (1) ab+bd=2b (2) ac+cd=2c (3) bc+d^2 =2d (4) 4 variables and 4 equation from (1) and (4) a^2 −d^2 =2(a−d)⇒a=d or a+d=2 case 1 a=d from (2) db+bd=2b⇒b=0 or d=1 1a. case b=0 from (4) d^2 =2d⇒d=0 or d=2 1aa∙ case d=0 a=b=c=d=0 ....(A) 1ab. csse d=2 a=d=2 ac+dc=2c⇒2(√2)c=2c⇒c=0 a=d=2, b=c=0 (B) 1b. case d=1 a=d=1, bc=1 ...(C) case 2: a+d=2 b, c can take any vale (D) To satiafy A^2 =2A solution are (Sol A) a=b=c=d=0 this satisifies genral condtion (Sol B) a=d=2, b=c=0 to be checked for higher powers. (Sol C) a=d=1, cb=1 to be checked for higher powers. (Sol D) b,c a, d=1−a to be checked for higher powers. Continue

$${A}^{\mathrm{2}} =\begin{pmatrix}{{a}^{\mathrm{2}} +{bc}}&{{ab}+{bd}}\\{{ac}+{cd}}&{{bc}+{d}^{\mathrm{2}} }\end{pmatrix}\:=\begin{pmatrix}{\mathrm{2}{a}}&{\mathrm{2}{b}}\\{\mathrm{2}{c}}&{\mathrm{2}{d}}\end{pmatrix} \\ $$$${a}^{\mathrm{2}} +{bc}=\mathrm{2}{a}\:\:\:\left(\mathrm{1}\right) \\ $$$${ab}+{bd}=\mathrm{2}{b}\:\:\:\left(\mathrm{2}\right) \\ $$$${ac}+{cd}=\mathrm{2}{c}\:\:\:\left(\mathrm{3}\right) \\ $$$${bc}+{d}^{\mathrm{2}} =\mathrm{2}{d}\:\:\:\left(\mathrm{4}\right) \\ $$$$\mathrm{4}\:{variables}\:{and}\:\mathrm{4}\:{equation} \\ $$$${from}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{4}\right) \\ $$$${a}^{\mathrm{2}} −{d}^{\mathrm{2}} =\mathrm{2}\left({a}−{d}\right)\Rightarrow{a}={d}\:{or}\:{a}+{d}=\mathrm{2} \\ $$$${case}\:\mathrm{1}\:{a}={d} \\ $$$${from}\:\left(\mathrm{2}\right)\:{db}+{bd}=\mathrm{2}{b}\Rightarrow{b}=\mathrm{0}\:{or}\:{d}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\mathrm{1}{a}.\:{case}\:{b}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{from}\:\left(\mathrm{4}\right)\:{d}^{\mathrm{2}} =\mathrm{2}{d}\Rightarrow{d}=\mathrm{0}\:{or}\:{d}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}{aa}\centerdot\:\mathrm{case}\:{d}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}={b}={c}={d}=\mathrm{0}\:\:\:....\left({A}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}{ab}.\:{csse}\:{d}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}={d}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ac}+{dc}=\mathrm{2}{c}\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}{c}=\mathrm{2}{c}\Rightarrow{c}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}={d}=\mathrm{2},\:{b}={c}=\mathrm{0}\:\:\:\:\left({B}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{1}{b}.\:{case}\:{d}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}={d}=\mathrm{1},\:{bc}=\mathrm{1}\:\:\:...\left({C}\right) \\ $$$${case}\:\mathrm{2}:\:{a}+{d}=\mathrm{2} \\ $$$$\:\:\:\:{b},\:{c}\:{can}\:{take}\:{any}\:{vale}\:\left({D}\right) \\ $$$$\mathrm{To}\:\mathrm{satiafy}\:{A}^{\mathrm{2}} =\mathrm{2}{A}\:\mathrm{solution}\:\mathrm{are} \\ $$$$\left({S}\mathrm{ol}\:{A}\right)\:{a}={b}={c}={d}=\mathrm{0}\:{th}\mathrm{is}\:\mathrm{satisifies}\:\mathrm{genral}\:\mathrm{condtion} \\ $$$$\left(\mathrm{Sol}\:\mathrm{B}\right)\:{a}={d}=\mathrm{2},\:{b}={c}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{to}\:{be}\:{checked}\:{for}\:{higher}\:{powers}. \\ $$$$\left(\mathrm{Sol}\:\mathrm{C}\right)\:{a}={d}=\mathrm{1},\:{cb}=\mathrm{1} \\ $$$$\:\:\:\:\:\:{to}\:{be}\:{checked}\:{for}\:{higher}\:{powers}. \\ $$$$\left(\mathrm{Sol}\:\mathrm{D}\right)\:{b},{c}\:{a},\:{d}=\mathrm{1}−{a} \\ $$$$\:\:\:\:\:{to}\:{be}\:{checked}\:{for}\:{higher}\:{powers}. \\ $$$$\mathrm{Continue} \\ $$

Answered by prakash jain last updated on 15/Dec/15

A= ((2,0),(0,2) ) A^2 = ((4,0),(0,4) ) A^n = ((2^n ,0),(0,2^n ) ) does not satisfy general comdition. so a=b=c=d=0 is solution a=d=2,b=d=0 is not solution. Sol (C) and (D) to be checked.

$${A}=\begin{pmatrix}{\mathrm{2}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\:{A}^{\mathrm{2}} =\begin{pmatrix}{\mathrm{4}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{4}}\end{pmatrix}\:{A}^{{n}} =\begin{pmatrix}{\mathrm{2}^{{n}} }&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{2}^{{n}} }\end{pmatrix} \\ $$$${does}\:{not}\:{satisfy}\:{general}\:{comdition}. \\ $$$${so}\: \\ $$$${a}={b}={c}={d}=\mathrm{0}\:{is}\:{solution} \\ $$$${a}={d}=\mathrm{2},{b}={d}=\mathrm{0}\:{is}\:{not}\:{solution}. \\ $$$${S}\mathrm{ol}\:\left(\mathrm{C}\right)\:\mathrm{and}\:\left(\mathrm{D}\right)\:\mathrm{to}\:\mathrm{be}\:\mathrm{checked}. \\ $$

Answered by prakash jain last updated on 15/Dec/15

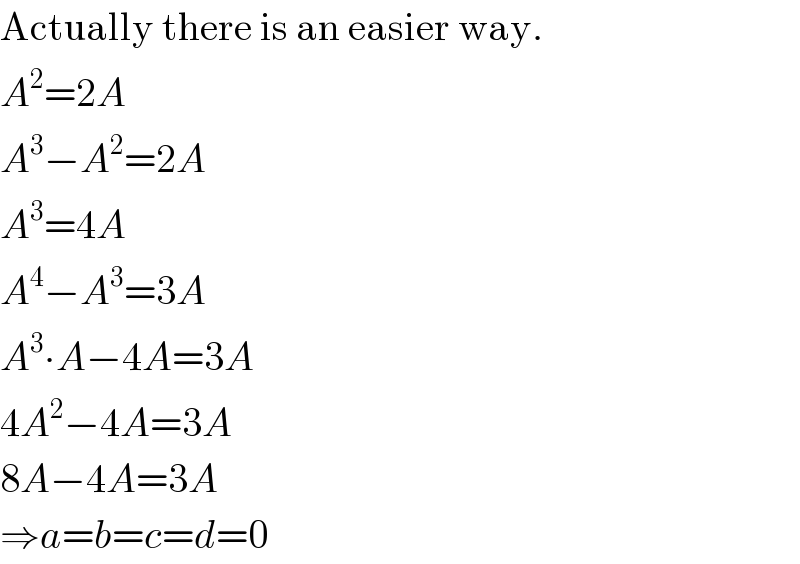
Actually there is an easier way. A^2 =2A A^3 −A^2 =2A A^3 =4A A^4 −A^3 =3A A^3 ∙A−4A=3A 4A^2 −4A=3A 8A−4A=3A ⇒a=b=c=d=0

$$\mathrm{Actually}\:\mathrm{there}\:\mathrm{is}\:\mathrm{an}\:\mathrm{easier}\:\mathrm{way}. \\ $$$${A}^{\mathrm{2}} =\mathrm{2}{A} \\ $$$${A}^{\mathrm{3}} −{A}^{\mathrm{2}} =\mathrm{2}{A} \\ $$$${A}^{\mathrm{3}} =\mathrm{4}{A} \\ $$$${A}^{\mathrm{4}} −{A}^{\mathrm{3}} =\mathrm{3}{A} \\ $$$${A}^{\mathrm{3}} \centerdot{A}−\mathrm{4}{A}=\mathrm{3}{A} \\ $$$$\mathrm{4}{A}^{\mathrm{2}} −\mathrm{4}{A}=\mathrm{3}{A} \\ $$$$\mathrm{8}{A}−\mathrm{4}{A}=\mathrm{3}{A} \\ $$$$\Rightarrow{a}={b}={c}={d}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com