Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 37339 by math khazana by abdo last updated on 12/Jun/18

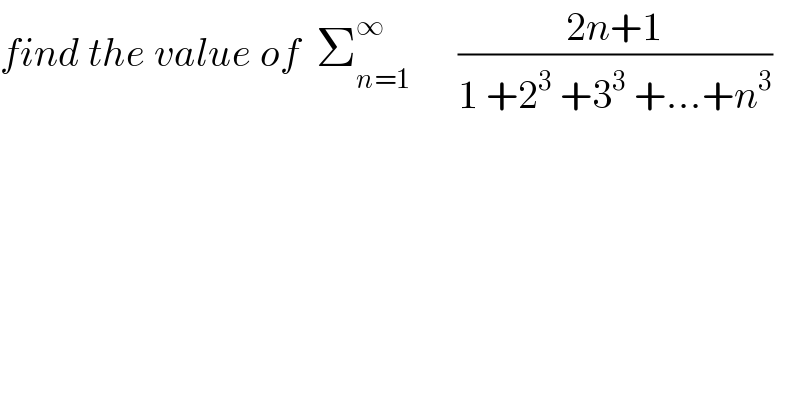
find the value of Σ_(n=1) ^∞ ((2n+1)/(1 +2^3 +3^3 +...+n^3 ))

$${find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\:\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{1}\:+\mathrm{2}^{\mathrm{3}} \:+\mathrm{3}^{\mathrm{3}} \:+...+{n}^{\mathrm{3}} } \\ $$

Commented by math khazana by abdo last updated on 13/Jun/18

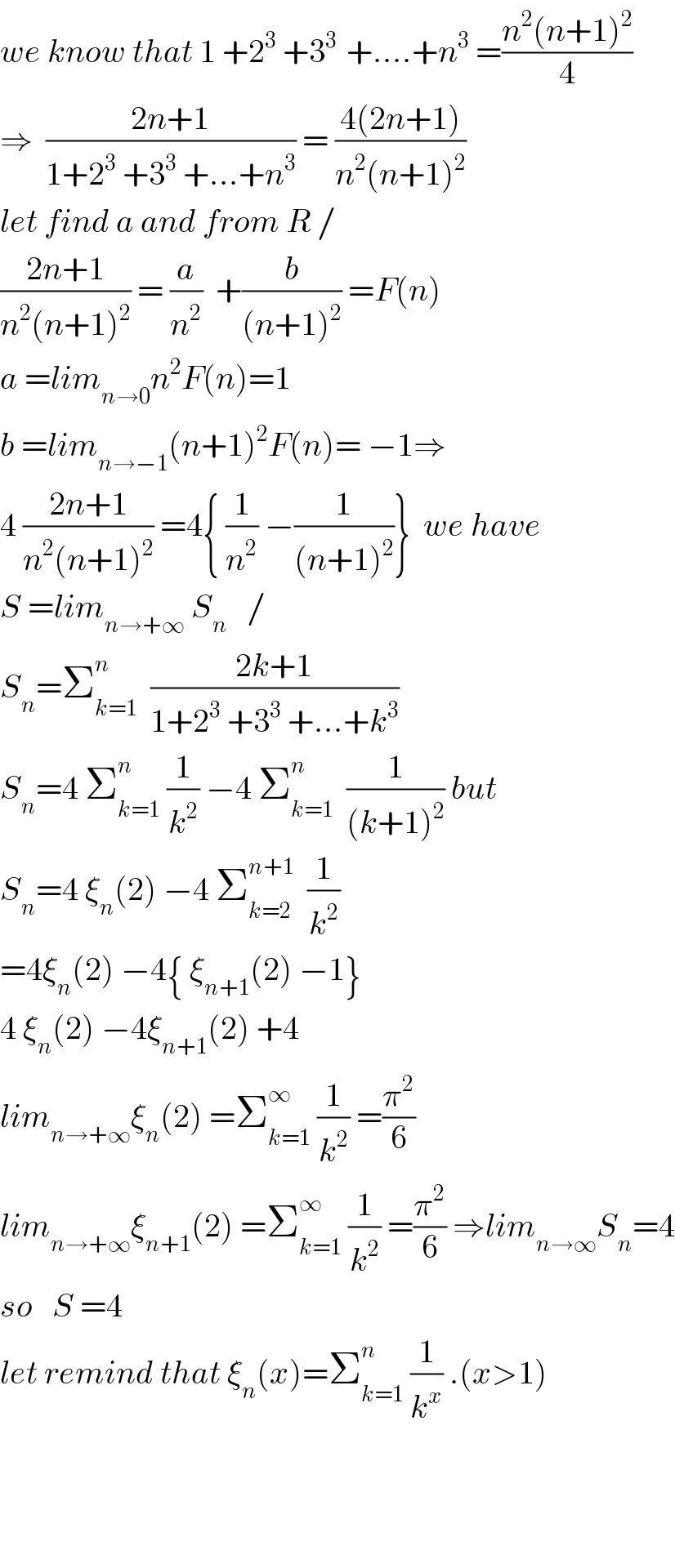
we know that 1 +2^3 +3^(3 ) +....+n^3 =((n^2 (n+1)^2 )/4) ⇒ ((2n+1)/(1+2^3 +3^3 +...+n^3 )) = ((4(2n+1))/(n^2 (n+1)^2 )) let find a and from R / ((2n+1)/(n^2 (n+1)^2 )) = (a/n^2 ) +(b/((n+1)^2 )) =F(n) a =lim_(n→0) n^2 F(n)=1 b =lim_(n→−1) (n+1)^2 F(n)= −1⇒ 4 ((2n+1)/(n^2 (n+1)^2 )) =4{ (1/n^2 ) −(1/((n+1)^2 ))} we have S =lim_(n→+∞) S_n / S_n =Σ_(k=1) ^n ((2k+1)/(1+2^3 +3^3 +...+k^3 )) S_n =4 Σ_(k=1) ^n (1/k^2 ) −4 Σ_(k=1) ^n (1/((k+1)^2 )) but S_n =4 ξ_n (2) −4 Σ_(k=2) ^(n+1) (1/k^2 ) =4ξ_n (2) −4{ ξ_(n+1) (2) −1} 4 ξ_n (2) −4ξ_(n+1) (2) +4 lim_(n→+∞) ξ_n (2) =Σ_(k=1) ^∞ (1/k^2 ) =(π^2 /6) lim_(n→+∞) ξ_(n+1) (2) =Σ_(k=1) ^∞ (1/k^2 ) =(π^2 /6) ⇒lim_(n→∞) S_n =4 so S =4 let remind that ξ_n (x)=Σ_(k=1) ^n (1/k^x ) .(x>1)

$${we}\:{know}\:{that}\:\mathrm{1}\:+\mathrm{2}^{\mathrm{3}} \:+\mathrm{3}^{\mathrm{3}\:} \:+....+{n}^{\mathrm{3}} \:=\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\mathrm{3}} \:+\mathrm{3}^{\mathrm{3}} \:+...+{n}^{\mathrm{3}} }\:=\:\frac{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${let}\:{find}\:{a}\:{and}\:{from}\:{R}\:/ \\ $$$$\frac{\mathrm{2}{n}+\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{{a}}{{n}^{\mathrm{2}} }\:\:+\frac{{b}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:={F}\left({n}\right) \\ $$$${a}\:={lim}_{{n}\rightarrow\mathrm{0}} {n}^{\mathrm{2}} {F}\left({n}\right)=\mathrm{1} \\ $$$${b}\:={lim}_{{n}\rightarrow−\mathrm{1}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} {F}\left({n}\right)=\:−\mathrm{1}\Rightarrow \\ $$$$\mathrm{4}\:\frac{\mathrm{2}{n}+\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{4}\left\{\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right\}\:\:{we}\:{have} \\ $$$${S}\:={lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \:\:\:/ \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\mathrm{3}} \:+\mathrm{3}^{\mathrm{3}} \:+...+{k}^{\mathrm{3}} } \\ $$$${S}_{{n}} =\mathrm{4}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:−\mathrm{4}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:{but} \\ $$$${S}_{{n}} =\mathrm{4}\:\xi_{{n}} \left(\mathrm{2}\right)\:−\mathrm{4}\:\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$=\mathrm{4}\xi_{{n}} \left(\mathrm{2}\right)\:−\mathrm{4}\left\{\:\xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)\:−\mathrm{1}\right\} \\ $$$$\mathrm{4}\:\xi_{{n}} \left(\mathrm{2}\right)\:−\mathrm{4}\xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)\:+\mathrm{4} \\ $$$${lim}_{{n}\rightarrow+\infty} \xi_{{n}} \left(\mathrm{2}\right)\:=\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$${lim}_{{n}\rightarrow+\infty} \xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)\:=\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow{lim}_{{n}\rightarrow\infty} {S}_{{n}} =\mathrm{4} \\ $$$${so}\:\:\:{S}\:=\mathrm{4} \\ $$$${let}\:{remind}\:{that}\:\xi_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{{x}} }\:.\left({x}>\mathrm{1}\right)\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com