
Question Number 39019 by maxmathsup by imad last updated on 01/Jul/18
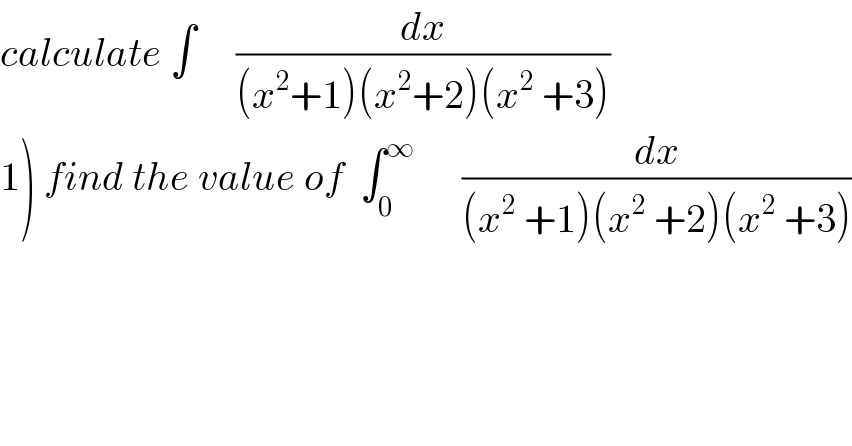
$${calculate}\:\int\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$
Commented by math khazana by abdo last updated on 02/Jul/18
![2) ∫_0 ^(+∞) F(x)dx =[(1/2)arctan(x)−(1/(2(√2)))arctan((x/(√2))) +(1/(2(√3))) arctan((x/(√3)))]_0 ^(+∞) =(π/4) −(1/(2(√2))) (π/2) +(1/(2(√3))) (π/2) =(π/4) −(π/(4(√2))) +(π/(4(√3))) .](Q39114.png)
$$\left.\mathrm{2}\right)\:\:\int_{\mathrm{0}} ^{+\infty} \:{F}\left({x}\right){dx}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{arctan}\left(\frac{{x}}{\sqrt{\mathrm{2}}}\right)\right. \\ $$$$\left.+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{{x}}{\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{4}}\:−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{3}}}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 02/Jul/18
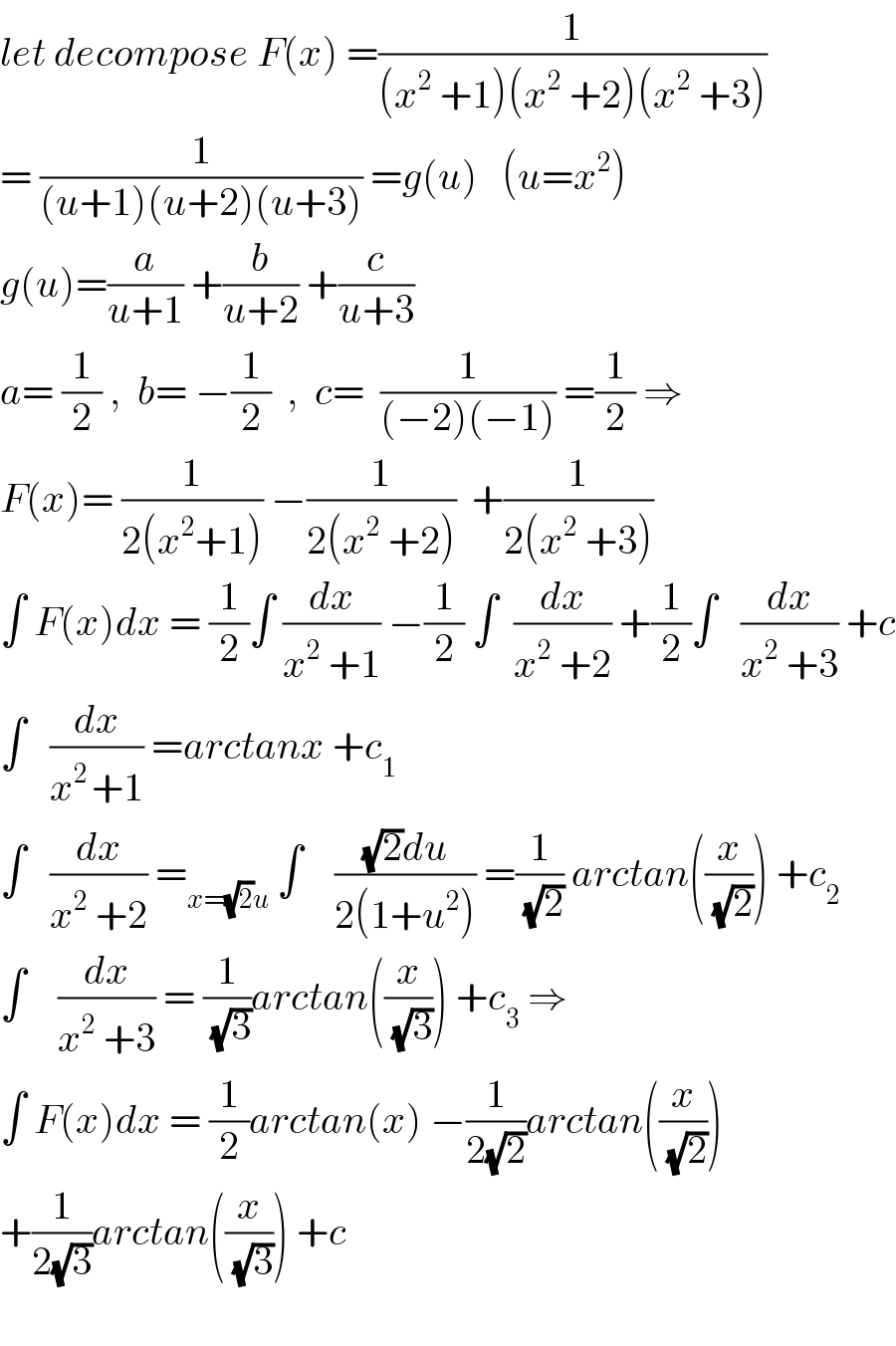
$${let}\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\left({u}+\mathrm{1}\right)\left({u}+\mathrm{2}\right)\left({u}+\mathrm{3}\right)}\:={g}\left({u}\right)\:\:\:\left({u}={x}^{\mathrm{2}} \right) \\ $$$${g}\left({u}\right)=\frac{{a}}{{u}+\mathrm{1}}\:+\frac{{b}}{{u}+\mathrm{2}}\:+\frac{{c}}{{u}+\mathrm{3}} \\ $$$${a}=\:\frac{\mathrm{1}}{\mathrm{2}}\:,\:\:{b}=\:−\frac{\mathrm{1}}{\mathrm{2}}\:\:,\:\:{c}=\:\:\frac{\mathrm{1}}{\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)}\:\:+\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$$\int\:{F}\left({x}\right){dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{3}}\:+{c} \\ $$$$\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}\:} +\mathrm{1}}\:={arctanx}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}}\:=_{{x}=\sqrt{\mathrm{2}}{u}} \:\int\:\:\:\:\frac{\sqrt{\mathrm{2}}{du}}{\mathrm{2}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{arctan}\left(\frac{{x}}{\sqrt{\mathrm{2}}}\right)\:+{c}_{\mathrm{2}} \\ $$$$\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{3}}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}{arctan}\left(\frac{{x}}{\sqrt{\mathrm{3}}}\right)\:+{c}_{\mathrm{3}} \:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({x}\right)\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{arctan}\left(\frac{{x}}{\sqrt{\mathrm{2}}}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{arctan}\left(\frac{{x}}{\sqrt{\mathrm{3}}}\right)\:+{c}\: \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 03/Jul/18

$$\left.\mathrm{2}\right)\:{Residus}\:{method}\:{let}\:{I}=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}\:} +\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$$\mathrm{2}{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$${let}\:\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{2}\right)\left({z}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:{i},−{i},{i}\sqrt{\mathrm{2}},−{i}\sqrt{\mathrm{2}},{i}\sqrt[{�}]{\mathrm{3}},−{i}\sqrt{\mathrm{3}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,{i}\sqrt{\mathrm{2}}\right)+{Res}\left(\bar {\varphi},−{i}\sqrt{\mathrm{3}}\right)\right\} \\ $$$$\varphi\left({z}\right)\:\:=\frac{\mathrm{1}}{\left({z}−{i}\right)\left({z}+{i}\right)\left({z}−{i}\sqrt{\mathrm{2}}\right)\left({z}+{i}\sqrt{\mathrm{2}}\right)\left({z}+{i}\sqrt{\mathrm{3}}\right)\left({z}−{i}\sqrt{\mathrm{3}}\right)} \\ $$$${Res}\left(\varphi,{i}\right)\:=\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)\left(\mathrm{1}\right)\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{4}{i}} \\ $$$${Res}\left(\varphi,{i}\sqrt{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{2}{i}\sqrt{\mathrm{2}}\right)\left(−\mathrm{1}\right)\left(\mathrm{1}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{2}}} \\ $$$${Res}\left(\varphi,{i}\sqrt{\mathrm{3}}\right)\:=\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}\right)\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{\mathrm{1}}{\mathrm{4}{i}}\:−\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{3}}}\right\} \\ $$$$=\:\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\sqrt{\mathrm{2}}}\:+\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${I}\:=\:\frac{\pi}{\mathrm{4}}\:−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{3}}}\:. \\ $$
Answered by behi83417@gmail.com last updated on 03/Jul/18
![I=(1/3)∫((2(x^2 +3)−(x^2 +1)−(x^2 +2))/((x^2 +1)(x^2 +2)(x^2 +3)))dx= =(1/3)∫[(2/((x^2 +1)(x^2 +2)))−(1/((x^2 +2)(x^2 +3)))−(1/((x^2 +1)(x^2 +3)))]dx= =(1/3)∫[2((1/(x^2 +1))−(1/(x^2 +2)))+(1/(x^2 +3))−(1/(x^2 +2))−(1/2)((1/(x^2 +1))−(1/(x^2 +3)))]dx= =(1/3)∫[(3/(2(x^2 +1)))−(3/(2(x^2 +1)))+(3/(2(x^2 +3)))]dx= =(1/2)tg^(−1) x−(1/(2(√2)))tg^(−1) (x/(√2))+(1/(2(√3)))tg^(−1) (x/(√3))+const. 2)∫_0 ^∞ f(x)dx=((1/2)−(1/(2(√2)))+(1/(2(√3)))).(π/2)= =(π/4)−(π/(4(√2)))+(π/(4(√3))).■](Q39031.png)
$${I}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{3}\right)−\left({x}^{\mathrm{2}} +\mathrm{1}\right)−\left({x}^{\mathrm{2}} +\mathrm{2}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\left[\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}\right]{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\left[\mathrm{2}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}\right)+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)\right]{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\left[\frac{\mathrm{3}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{3}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}\right]{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{tg}^{−\mathrm{1}} {x}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tg}^{−\mathrm{1}} \frac{{x}}{\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tg}^{−\mathrm{1}} \frac{{x}}{\sqrt{\mathrm{3}}}+{const}. \\ $$$$\left.\mathrm{2}\right)\underset{\mathrm{0}} {\overset{\infty} {\int}}{f}\left({x}\right){dx}=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\right).\frac{\pi}{\mathrm{2}}= \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{3}}}.\blacksquare \\ $$
