Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 39300 by behi83417@gmail.com last updated on 05/Jul/18

	Answered by MrW3 last updated on 05/Jul/18

	$a s q u a r e c a n i n s c r i b e e v e r y t r i a n g l e .$ $s o t h e q u e s t i o n i s$ $i f i t i s p o s s i b l e t o b u i l d a t r i a n g l e$ $w h o s e s i d e s a r e t h r e e c o n s e c u t i v e o d d$ $(o r e v e n) n u m b e r s .$ $a = n$ $b = n + 2$ $c = n + 4$ $f o r t h i s t o b e p o s s i b l e, w e m u s t h a v e$ $a + b > c \Rightarrow 2 n + 2 > n + 4 \Rightarrow n > 2$ $b + c > a \Rightarrow 2 n + 6 > n \Rightarrow n > - 6$ $c + a > b \Rightarrow 2 n + 4 > n + 2 \Rightarrow n > - 2$ $t h a t m e a n s n ⩾ 3 .$ $s o t h e a n s w e r i s y e s .$ $i f a d d i t i o n a l l y t h e t r i a n g l e s h o u l d o n l y$ $h a v e a c u t e a n g l e s, w e m u s t h a v e$ ${(n + 4)}^{2} ⩽ n^{2} + {(n + 2)}^{2}$ $n^{2} + 8 n + 16 ⩽ n^{2} + n^{2} + 4 n + 4$ $n^{2} - 4 n - 12 ⩾ 0$ $(n + 2) (n - 6) ⩾ 0$ $n ⩾ 6$
	Commented by behi83417@gmail.com last updated on 05/Jul/18

	$d e a r m a s t e r! t h a n k s a l o t . I g o t t h e$ $a n s w e r .$ $c a n w e p r o v e t h e f i r s t s t a t e m e n t ?$
	Commented by MrW3 last updated on 05/Jul/18

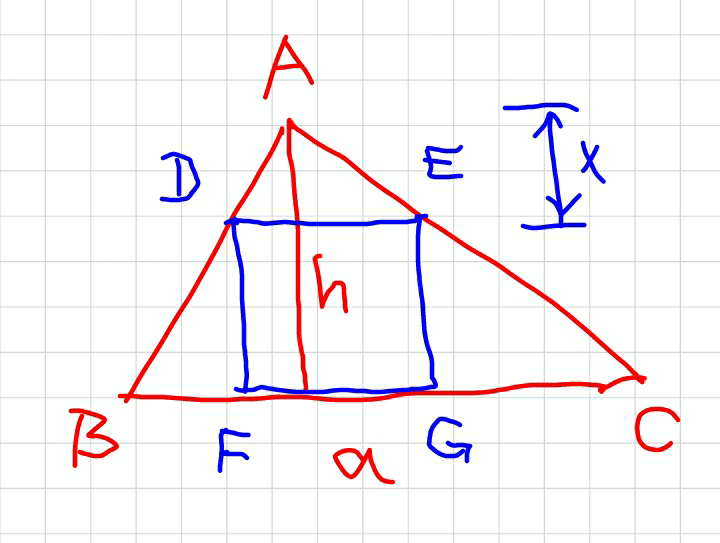
	$S t a t e m e n t :$ $I n e v e r y t r i a n g l e i t i s p o s s i b l e t o$ $f i n d a n i n s c r i b i n g s q u a r e .$ $P r o o f :$ $I n e v e r y t r i a n g l e t h e r e a r e a t l e a s t$ $t w o a c u t e a n g l e s . A s s u m e t h e s i d e$ $l e n g t h b e t w e e n t h e s e t w o a c u t e a n g l e s$ $i s a, a n d c o r r e s p o n d i n g a l t i t u d e i s h .$ $D E = \frac{x}{h} \times a$ $D F = h - x$ $D E = D F$ $\frac{x}{h} a = h - x$ $\Rightarrow x = \frac{h}{h + a} \times h$ $0 < x < h$ $i . e . t h e r e i s a x = \frac{h}{h + a} \times a w i t h w h i c h$ $D E G F i s a s q u a r e .$ $S i n c e ∠ B a n d ∠ C a r e a c u t e,$ $\Rightarrow F a n d G l i e o n t h e s i d e B C,$ $i . e . D E G F i s a n i n s c r i b i n g s q u a r e .$
	Commented by MrW3 last updated on 05/Jul/18

	Commented by behi83417@gmail.com last updated on 05/Jul/18

	$t h a n k s i n a d v a n c e d e a r m a s t e r .$ $n i c e p r o o f . I t h i n k i t i s t h e f i r s t p r o o f$ $t o t h i s s t a t e m e n t .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum