
Question Number 39369 by maxmathsup by imad last updated on 05/Jul/18
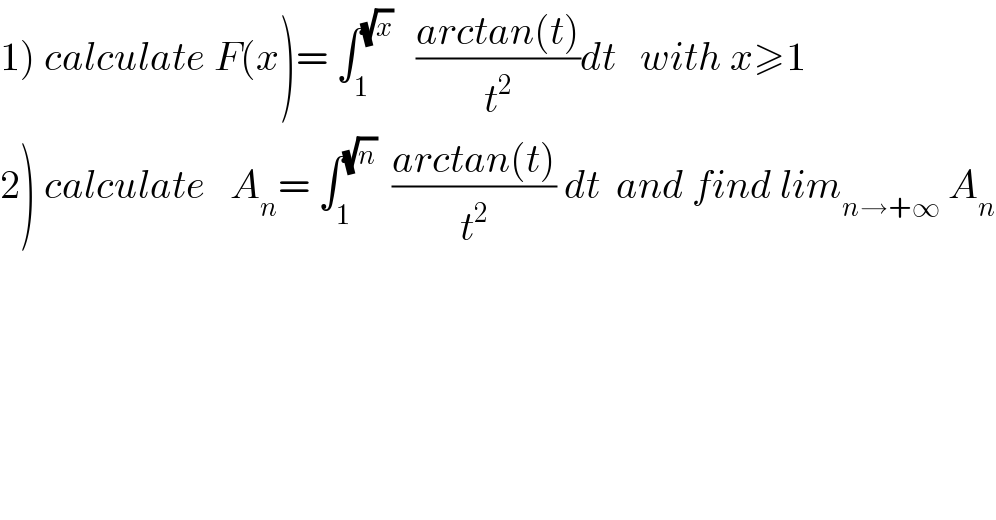
$$\left.\mathrm{1}\right)\:{calculate}\:{F}\left({x}\right)=\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} }{dt}\:\:\:{with}\:{x}\geqslant\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\:{A}_{{n}} =\:\int_{\mathrm{1}} ^{\sqrt{{n}}} \:\:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} }\:{dt}\:\:{and}\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$
Commented by math khazana by abdo last updated on 07/Jul/18
![1) by parts F(x) =[−(1/t) arctant]_1 ^(√x) −∫_1 ^(√x) ((−1)/(t(1+t^2 )))dt =(π/4) −((arctan((√x)))/(√x)) + ∫_1 ^(√x) ( (1/t) −(t/(1+t^2 )))dt =(π/4) −((arctan((√x)))/(√x)) +ln((√x)) −(1/2)[ln(1+t^2 )]_1 ^(√x) =(π/4) −((arctan((√x)))/(√x)) +ln((√x)) −(1/2){ln(1+x)−ln(2)} 2) we have A_n =F(n) =(π/4) −((arctan((√n)))/(√n)) + ln((√n)) −ln(√(1+n)) +((ln(2))/2) =(π/4) +((ln(2))/2) +ln(((√n)/(√(n+1)))) −((arctan((√(n))))/(√n)) ⇒ lim_(n→+∞) A_n =(π/4) +((ln(2))/2) .](Q39543.png)
$$\left.\mathrm{1}\right)\:{by}\:{parts}\:{F}\left({x}\right)\:=\left[−\frac{\mathrm{1}}{{t}}\:{arctant}\right]_{\mathrm{1}} ^{\sqrt{{x}}} \:−\int_{\mathrm{1}} ^{\sqrt{{x}}} \frac{−\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{\sqrt{{x}}}\:+\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \left(\:\frac{\mathrm{1}}{{t}}\:−\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{\sqrt{{x}}}\:\:+{ln}\left(\sqrt{{x}}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]_{\mathrm{1}} ^{\sqrt{{x}}} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{\sqrt{{x}}}\:+{ln}\left(\sqrt{{x}}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{2}\right)\right\} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{A}_{{n}} ={F}\left({n}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{{arctan}\left(\sqrt{{n}}\right)}{\sqrt{{n}}}\:+\:{ln}\left(\sqrt{{n}}\right)\:−{ln}\sqrt{\mathrm{1}+{n}}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\:+{ln}\left(\frac{\sqrt{{n}}}{\sqrt{{n}+\mathrm{1}}}\right)\:−\frac{{arctan}\left(\sqrt{\left.{n}\right)}\right.}{\sqrt{{n}}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\frac{\pi}{\mathrm{4}}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:. \\ $$
