Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 40829 by math khazana by abdo last updated on 28/Jul/18

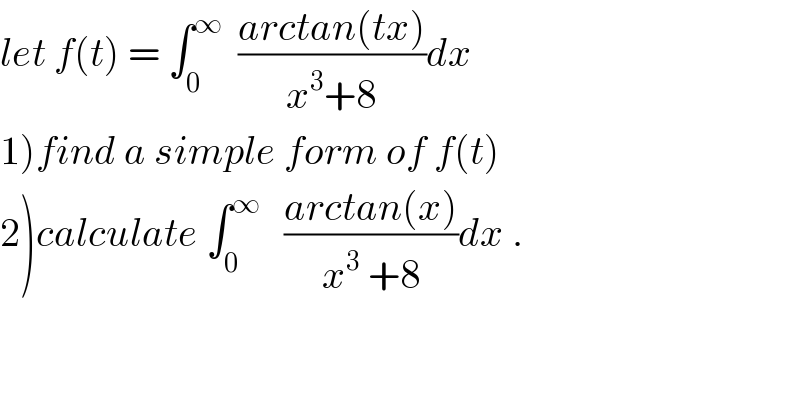
let f(t) = ∫_0 ^∞ ((arctan(tx))/(x^3 +8))dx 1)find a simple form of f(t) 2)calculate ∫_0 ^∞ ((arctan(x))/(x^3 +8))dx .

$${let}\:{f}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({tx}\right)}{{x}^{\mathrm{3}} +\mathrm{8}}{dx} \\ $$$$\left.\mathrm{1}\right){find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({t}\right) \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}\right)}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx}\:. \\ $$

Answered by maxmathsup by imad last updated on 29/Jul/18

1) we have f^′ (t) = ∫_0 ^∞ (x/((1+t^2 x^2 )(x^3 +8)))dx =_(tx =α) ∫_0 ^∞ (1/((1+α^2 )((α^3 /t^3 ) +8)))(α/t) (dα/t) =(1/t^2 )∫_0 ^∞ t^3 ((αdα)/((1+α^2 )(α^3 +8t^3 ))) = t ∫_0 ^∞ ((xdx)/((x^2 +1)(x^3 +8t^3 ))) let decompose F(x)=(x/((x^2 +1)(x^3 +8t^3 ))) F(x) = (x/((x^2 +1)(x+2t)(x^2 −2xt +4t^2 ))) =(a/(x+2t)) +((bx+c)/(x^2 +1)) +((dx+e)/(x^2 −2xt +4t^2 )) a =lim_(x→−2t) (x+2t)F(x)= ((−2t)/((4t^2 +1)(12t^2 ))) = ((−1)/(6t(4t^2 +1))) lim_(x→+∞) xF(x)=0 =a +b +d ⇒b+d =−a F(o) =0 =(a/(2t)) +c +(e/(4t^2 )) ⇒2at +4t^2 c +e =0 ....be continued...

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}}{\left(\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} +\mathrm{8}\right)}{dx}\:=_{{tx}\:=\alpha} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left(\frac{\alpha^{\mathrm{3}} }{{t}^{\mathrm{3}} }\:+\mathrm{8}\right)}\frac{\alpha}{{t}}\:\frac{{d}\alpha}{{t}} \\ $$$$=\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\:\:{t}^{\mathrm{3}} \:\:\frac{\alpha{d}\alpha}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left(\alpha^{\mathrm{3}} \:+\mathrm{8}{t}^{\mathrm{3}} \right)}\:=\:{t}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{xdx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{3}} +\mathrm{8}{t}^{\mathrm{3}} \right)}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\frac{{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{3}} +\mathrm{8}{t}^{\mathrm{3}} \right)} \\ $$$${F}\left({x}\right)\:=\:\:\frac{{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}+\mathrm{2}{t}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{xt}\:+\mathrm{4}{t}^{\mathrm{2}} \right)}\:=\frac{{a}}{{x}+\mathrm{2}{t}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{dx}+{e}}{{x}^{\mathrm{2}} \:−\mathrm{2}{xt}\:+\mathrm{4}{t}^{\mathrm{2}} } \\ $$$${a}\:={lim}_{{x}\rightarrow−\mathrm{2}{t}} \:\:\:\:\left({x}+\mathrm{2}{t}\right){F}\left({x}\right)=\:\frac{−\mathrm{2}{t}}{\left(\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{12}{t}^{\mathrm{2}} \right)}\:=\:\frac{−\mathrm{1}}{\mathrm{6}{t}\left(\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}\:={a}\:+{b}\:+{d}\:\Rightarrow{b}+{d}\:=−{a} \\ $$$${F}\left({o}\right)\:=\mathrm{0}\:=\frac{{a}}{\mathrm{2}{t}}\:+{c}\:+\frac{{e}}{\mathrm{4}{t}^{\mathrm{2}} }\:\Rightarrow\mathrm{2}{at}\:+\mathrm{4}{t}^{\mathrm{2}} {c}\:+{e}\:=\mathrm{0}\:....{be}\:{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com