Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 41291 by Mayur last updated on 04/Aug/18

Let ABCD be a parallelogram whose diagonals intersect at P and ley O be the origin, then OA^(→) +OB^(→) +OC^(→) +OD^(→) equals

$$\mathrm{Let}\:{ABCD}\:\mathrm{be}\:\mathrm{a}\:\mathrm{parallelogram}\:\mathrm{whose} \\ $$$$\mathrm{diagonals}\:\mathrm{intersect}\:\mathrm{at}\:{P}\:\mathrm{and}\:\mathrm{ley}\:{O}\:\mathrm{be} \\ $$$$\mathrm{the}\:\mathrm{origin},\:\mathrm{then}\:\overset{\rightarrow} {{OA}}+\overset{\rightarrow} {{OB}}+\overset{\rightarrow} {{OC}}+\overset{\rightarrow} {{OD}}\: \\ $$$$\mathrm{equals} \\ $$

Answered by MJS last updated on 04/Aug/18

4OP^(⇀)

$$\mathrm{4}\overset{\rightharpoonup} {{OP}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18

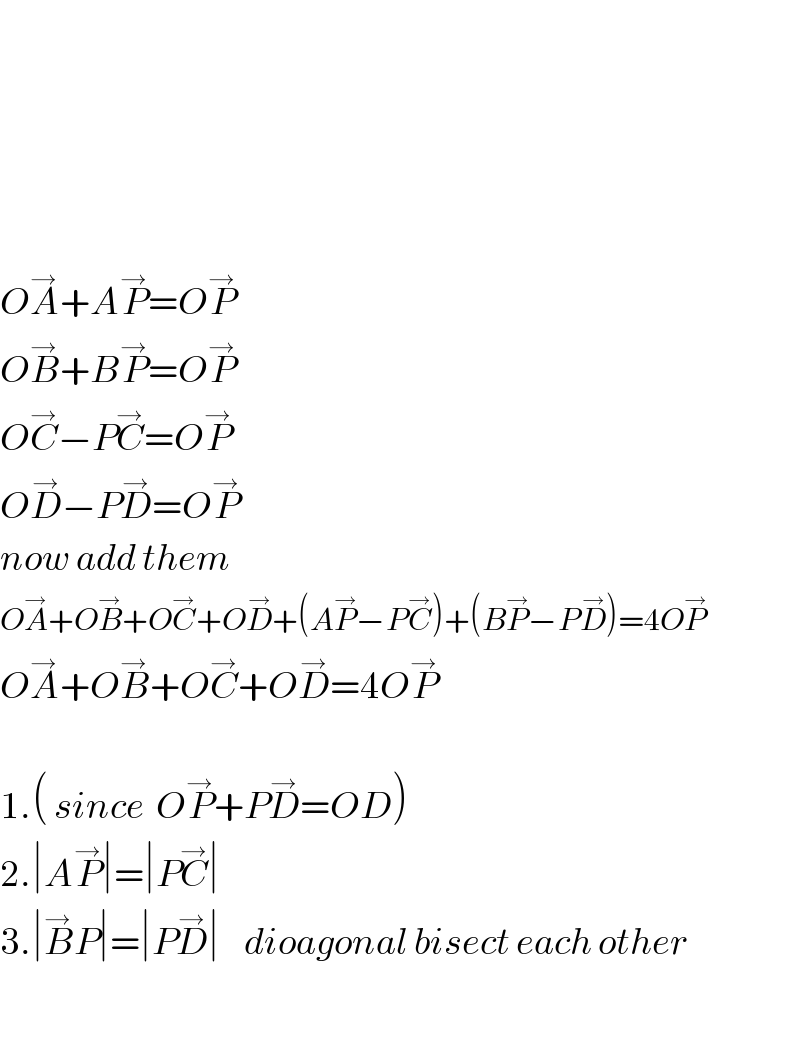
OA^→ +AP^→ =OP^→ OB^→ +BP^→ =OP^→ OC^→ −PC^→ =OP^→ OD^→ −PD^→ =OP^→ now add them OA^→ +OB^→ +OC^→ +OD^→ +(AP^→ −PC^→ )+(BP^→ −PD^→ )=4OP^→ OA^→ +OB^→ +OC^→ +OD^→ =4OP^→ 1.( since OP^→ +PD^→ =OD) 2.∣AP^→ ∣=∣PC^→ ∣ 3.∣B^→ P∣=∣PD^→ ∣ dioagonal bisect each other

$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${O}\overset{\rightarrow} {{A}}+{A}\overset{\rightarrow} {{P}}={O}\overset{\rightarrow} {{P}} \\ $$$${O}\overset{\rightarrow} {{B}}+{B}\overset{\rightarrow} {{P}}={O}\overset{\rightarrow} {{P}} \\ $$$${O}\overset{\rightarrow} {{C}}−{P}\overset{\rightarrow} {{C}}={O}\overset{\rightarrow} {{P}}\: \\ $$$${O}\overset{\rightarrow} {{D}}−{P}\overset{\rightarrow} {{D}}={O}\overset{\rightarrow} {{P}}\:\: \\ $$$${now}\:{add}\:{them} \\ $$$${O}\overset{\rightarrow} {{A}}+{O}\overset{\rightarrow} {{B}}+{O}\overset{\rightarrow} {{C}}+{O}\overset{\rightarrow} {{D}}+\left({A}\overset{\rightarrow} {{P}}−{P}\overset{\rightarrow} {{C}}\right)+\left({B}\overset{\rightarrow} {{P}}−{P}\overset{\rightarrow} {{D}}\right)=\mathrm{4}{O}\overset{\rightarrow} {{P}} \\ $$$${O}\overset{\rightarrow} {{A}}+{O}\overset{\rightarrow} {{B}}+{O}\overset{\rightarrow} {{C}}+{O}\overset{\rightarrow} {{D}}=\mathrm{4}{O}\overset{\rightarrow} {{P}} \\ $$$$ \\ $$$$\mathrm{1}.\left(\:{since}\:\:{O}\overset{\rightarrow} {{P}}+{P}\overset{\rightarrow} {{D}}={OD}\right) \\ $$$$\mathrm{2}.\mid{A}\overset{\rightarrow} {{P}}\mid=\mid{P}\overset{\rightarrow} {{C}}\mid \\ $$$$\mathrm{3}.\mid\overset{\rightarrow} {{B}P}\mid=\mid{P}\overset{\rightarrow} {{D}}\mid\:\:\:\:{dioagonal}\:{bisect}\:{each}\:{other}\: \\ $$$$ \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com