
Question Number 41702 by abdo.msup.com last updated on 11/Aug/18
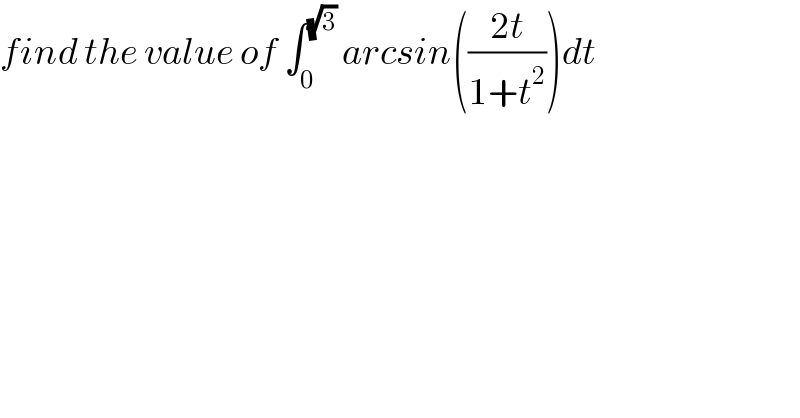
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:{arcsin}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt} \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
![let A = ∫_0 ^(√3) arcsin(((2t)/(1+t^2 )))dt changement t =tanθ give A = ∫_0 ^(π/3) arcsin(sin(2θ))(1+tan^2 θ)dθ =_(2θ=u) ∫_0 ^((2π)/3) arcsin(sinu)(1+tan^2 ((u/2)))du =∫_0 ^(π/2) u(1+tan^2 ((u/2)))du + ∫_(π/2) ^((2π)/3) arcsin(sinu)(1+tan^2 ((u/2)))du ∫_0 ^(π/2) u(1+tan^2 ((u/2)))du =[(u^2 /2)]_0 ^(π/2) +∫_0 ^(π/2) tan^2 ((u/2))du =(π^2 /8) + ∫_0 ^(π/2) (1+tan^2 ((u/2)))du −(π/2) = [2tan((u/2))]_0 ^(π/2) +(π^2 /8) −(π/2) =2 +(π^2 /8) −(π/2) also ∫_(π/2) ^((2π)/3) arcsin(sinu)(1+tan^2 ((u/2)))du =_(u=π−t) −∫_(π/2) ^(π/3) arcsin(sin(π−t))(1+tan^2 ((π/2)−(t/2)))dt = ∫_(π/3) ^(π/2) t{1 +(1/(tan^2 ((t/2))))}dt ( bijection at [−(π/2),(π/2)] = [(t^2 /2)]_(π/3) ^(π/2) + ∫_(π/3) ^(π/2) (t/(tan^2 ((t/2))))dt =( (π^2 /8) −(π^2 /(18))) + ∫_(π/3) ^(π/2) (t/(tan^2 ((t/2))))dt but ∫_(π/3) ^(π/2) (t/(tan^2 ((t/2))))dt =_((t/2)=u) ∫_(π/6) ^(π/4) ((2u)/(tan^2 (u))) 2du =4 ∫_(π/6) ^(π/4) (u/(tan^2 u)) du =_(tanu =α) 4 ∫_(1/(√3)) ^1 ((arctan(α))/α^2 ) (dα/(1+α^2 )) =4 ∫_(1/(√3)) ^1 ((arctan(α))/(α^2 (1+α^2 ))) dα ....be continued...](Q41755.png)
$${let}\:{A}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:{arcsin}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt}\:\:{changement} \\ $$$${t}\:={tan}\theta\:{give} \\ $$$${A}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\:{arcsin}\left({sin}\left(\mathrm{2}\theta\right)\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=_{\mathrm{2}\theta={u}} \:\:\:\int_{\mathrm{0}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \:{arcsin}\left({sinu}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {u}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right){du}\:+\:\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} {arcsin}\left({sinu}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right){du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {u}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right){du}\:\:=\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right){du} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\:\:+\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right){du}\:−\frac{\pi}{\mathrm{2}} \\ $$$$=\:\left[\mathrm{2}{tan}\left(\frac{{u}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\frac{\pi}{\mathrm{2}}\:=\mathrm{2}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\frac{\pi}{\mathrm{2}}\:{also} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \:{arcsin}\left({sinu}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right){du} \\ $$$$=_{{u}=\pi−{t}} \:\:\:\:\:−\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{3}}} \:\:{arcsin}\left({sin}\left(\pi−{t}\right)\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−\frac{{t}}{\mathrm{2}}\right)\right){dt} \\ $$$$=\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:{t}\left\{\mathrm{1}\:\:+\frac{\mathrm{1}}{{tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)}\right\}{dt}\:\:\left(\:\:{bijection}\:{at}\:\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right]\right. \\ $$$$=\:\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:+\:\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\frac{{t}}{{tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)}{dt} \\ $$$$=\left(\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}\right)\:+\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{t}}{{tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)}{dt}\:\:{but} \\ $$$$\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{t}}{{tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)}{dt}\:=_{\frac{{t}}{\mathrm{2}}={u}} \:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{\mathrm{2}{u}}{{tan}^{\mathrm{2}} \left({u}\right)}\:\mathrm{2}{du} \\ $$$$=\mathrm{4}\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{u}}{{tan}^{\mathrm{2}} {u}}\:{du}\:=_{{tanu}\:=\alpha} \:\:\:\mathrm{4}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\alpha\right)}{\alpha^{\mathrm{2}} }\:\frac{{d}\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$$=\mathrm{4}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\alpha\right)}{\alpha^{\mathrm{2}} \left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:{d}\alpha\:....{be}\:{continued}... \\ $$
Commented by alex041103 last updated on 12/Aug/18

$${You}\:{are}\:{wrong}.\:{When}\:{youmake}\:{the} \\ $$$${substitution}\:{t}={tan}\theta,\:{you}\:{have}\:{to}\:{multiply} \\ $$$${the}\:{integrand}\:{by}\:{a}\:{factor}\:{of}\:{sec}^{\mathrm{2}} \theta, \\ $$$${because}\:{dt}={sec}^{\mathrm{2}} \theta{d}\theta. \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
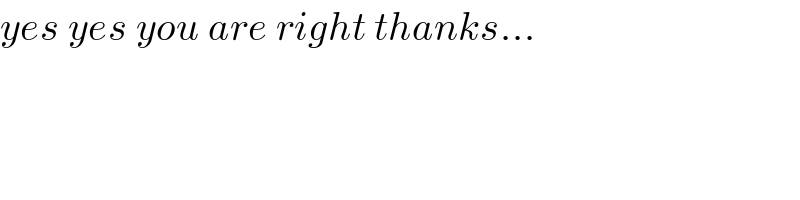
$${yes}\:{yes}\:{you}\:{are}\:{right}\:{thanks}... \\ $$
Answered by alex041103 last updated on 11/Aug/18
![let t=tan(x/2) dt=((sec^2 (x/2))/2)dx ⇒x=2arctan(t) ((2t)/(1+t^2 ))=sin(x)⇒∫_0 ^((2π)/3) xd(tan(x/2)) IBP ∫_0 ^((2π)/3) xd(tan(x/2))=[xtan(x/2)]_0 ^(2π/3) −2∫_0 ^(2π/3) tan(x/2)d(x/2)= =2(√3)π−2∫_0 ^( π/3) tan(u)du But ∫tan(x)dx=ln(sec x)+C ⇒ ∫_0 ^(√3) arcsin(((2t)/(1+t^2 )))dt=2(√3)π−2ln(((sec(π/3))/(sec(0))))= =2(√3)π−2ln(2) ∫_0 ^(√3) arcsin(((2t)/(1+t^2 )))dt=2(√3)π−2ln(2)](Q41714.png)
$${let}\:{t}={tan}\left({x}/\mathrm{2}\right)\:{dt}=\frac{{sec}^{\mathrm{2}} \left({x}/\mathrm{2}\right)}{\mathrm{2}}{dx}\:\Rightarrow{x}=\mathrm{2}{arctan}\left({t}\right) \\ $$$$\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }={sin}\left({x}\right)\Rightarrow\int_{\mathrm{0}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} {xd}\left({tan}\left({x}/\mathrm{2}\right)\right) \\ $$$${IBP} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} {xd}\left({tan}\left({x}/\mathrm{2}\right)\right)=\left[{xtan}\left({x}/\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi/\mathrm{3}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi/\mathrm{3}} {tan}\left({x}/\mathrm{2}\right){d}\left({x}/\mathrm{2}\right)= \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\pi−\mathrm{2}\int_{\mathrm{0}} ^{\:\pi/\mathrm{3}} {tan}\left({u}\right){du} \\ $$$${But}\:\int{tan}\left({x}\right){dx}={ln}\left({sec}\:{x}\right)+{C} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:{arcsin}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt}=\mathrm{2}\sqrt{\mathrm{3}}\pi−\mathrm{2}{ln}\left(\frac{{sec}\left(\pi/\mathrm{3}\right)}{{sec}\left(\mathrm{0}\right)}\right)= \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\pi−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:{arcsin}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt}=\mathrm{2}\sqrt{\mathrm{3}}\pi−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$
Commented by turbo msup by abdo last updated on 12/Aug/18
![sir alex you must divide the integral because arcsinx is defined from [−1,1] to [−(π/2),(π/2)](bijection) so your final result is not correct](Q41773.png)
$${sir}\:{alex}\:{you}\:{must}\:{divide}\:{the} \\ $$$${integral}\:{because}\:{arcsinx}\:{is} \\ $$$${defined}\:{from}\:\left[−\mathrm{1},\mathrm{1}\right]\:{to}\:\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right]\left({bijection}\right) \\ $$$${so}\:{your}\:{final}\:{result}\:{is}\:{not}\:{correct} \\ $$
Commented by alex041103 last updated on 12/Aug/18
![In that case it is perfectly OK. Because in the R arcsin(((2t)/(1+t^2 )))∈[−1,1]](Q41775.png)
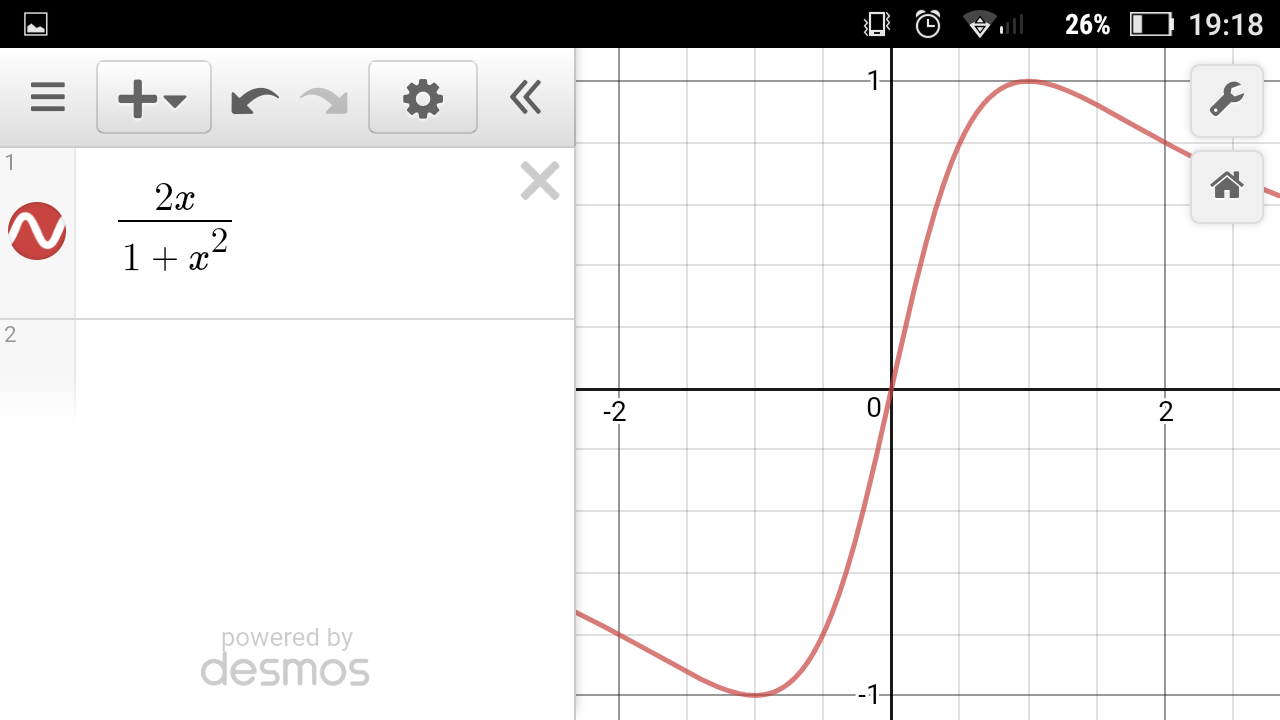
$${In}\:{that}\:{case}\:{it}\:{is}\:{perfectly}\:{OK}. \\ $$$${Because}\:{in}\:{the}\:\mathbb{R} \\ $$$${arcsin}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)\in\left[−\mathrm{1},\mathrm{1}\right] \\ $$
Commented by alex041103 last updated on 12/Aug/18
Commented by alex041103 last updated on 12/Aug/18

$${Oh}...{I}\:{understand}\:{what}\:{you}\:{mean}. \\ $$$${You}'{re}\:{actually}\:{right}.\:{But}... \\ $$$${there}\:{are}\:{different}\:{arcsin}\:{functions}. \\ $$$${for}\:{example}\:{there}\:{is}\:{one}\:{for}\:{which}\: \\ $$$${arcsin}\left({x}\right)\in\left[\mathrm{0},\mathrm{2}\pi\right)...{I}\:{thought}\:{that}\:{one} \\ $$$${was}\:{the}\:{one}\:{in}\:{the}\:{problem}....{a}\:{missunderstanding}.. \\ $$$${thank}\:{you}\:{for}\:{pointing}\:{it}\:{out}\:{for}\:{me}... \\ $$
