
Question Number 42654 by ajfour last updated on 30/Aug/18
Commented by ajfour last updated on 30/Aug/18

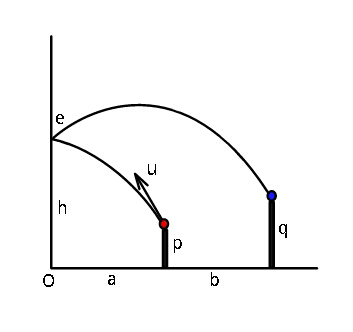
$${If}\:{the}\:{red}\:{ball}\:{is}\:{to}\:{hit}\:{the}\:{wall} \\ $$$${and}\:{then}\:{the}\:{blue}\:{ball},\:{find}\:{the} \\ $$$${speed}\:\boldsymbol{{u}}\:{and}\:{height}\:\boldsymbol{{h}}\:{where}\:{it} \\ $$$${hits}\:{the}\:{wall}.\:\left({coefficient}\:{of}\right. \\ $$$$\left.{restitution}\:{being}\:\boldsymbol{{e}}\right). \\ $$
Commented by MrW3 last updated on 03/Sep/18

$${the}\:{question}\:{could}\:{be}\:{modified}\:{to}: \\ $$$${find}\:{the}\:{smallest}\:{speed}\:{of}\:{the}\:{red}\:{ball} \\ $$$${such}\:{that}\:{it}\:{can}\:{hit}\:{the}\:{wall}\:{and}\:{then} \\ $$$${the}\:{blue}\:{ball}. \\ $$
Answered by MrW3 last updated on 04/Sep/18
)(1+tan^2 θ) q−p=(a+((a+b)/e)) tan θ−(a+((a+b)/e))^2 (g/(2u^2 ))(1+tan^2 θ) with A=a+((a+b)/e), B=q−p, λ=tan θ we get B=Aλ−A^2 (1+λ^2 )(g/(2u^2 )) ⇒u^2 =((gA^2 )/2)×((1+λ^2 )/(Aλ−B)) let f(λ)=((1+λ^2 )/(Aλ−B)) ((df(λ))/dλ)=((2λ)/(Aλ−B))−((A(1+λ^2 ))/((Aλ−B)^2 ))=0 ⇒((1+λ^2 )/(Aλ−B))=((2λ)/A) ⇒2λ(Aλ−B)−A(1+λ^2 )=0 ⇒Aλ^2 −2Bλ−A=0 ⇒λ=((B+(√(A^2 +B^2 )))/A)=((q−p)/(a+((a+b)/e)))+(√(1+(((q−p)/(a+((a+b)/e))))^2 )) ⇒u_(min) ^2 =((gA^2 )/2)×((2λ)/A)=g(B+(√(A^2 +B^2 ))) ⇒u_(min) =(√([(q−p)+(√((a+((a+b)/e))^2 +(q−p)^2 ))]g)) h_m =p+aλ−((a^2 g)/(2u_(min) ^2 ))(1+λ^2 ) h_m =p+aλ−((a^2 (1+λ^2 ))/(2Aλ)) h_m =p+aλ−((a^2 (Aλ−B))/A^2 ) h_m =p+a(1−(a/A))((B/A)+((√(A^2 +B^2 ))/A))+((a^2 B)/A^2 ) ⇒h_m =p+a(1−(a/(a+((a+b)/e))))[((q−p)/(a+((a+b)/e)))+(√(1+(((q−p)/(a+((a+b)/e))))^2 ))]+((a/(a+((a+b)/e))))^2 (q−p) θ_m =tan^(−1) λ ⇒θ_m =tan^(−1) [ ((q−p)/(a+((a+b)/e)))+(√(1+(((q−p)/(a+((a+b)/e))))^2 ))]](Q42740.png)
$${a}={u}\:\mathrm{cos}\:\theta\:{t}_{\mathrm{1}} \:\:\:...\left({i}\right) \\ $$$${h}−{p}={u}\:\mathrm{sin}\:\theta\:{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\:{g}\:{t}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:...\left({ii}\right) \\ $$$${a}+{b}=\:{eu}\:\mathrm{cos}\:\theta\:{t}_{\mathrm{2}} \:\:\:\:...\left({iii}\right) \\ $$$${q}−{h}=\left({u}\:\mathrm{sin}\:\theta−{g}\:{t}_{\mathrm{1}} \right)\:{t}_{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\:{g}\:{t}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:\:\:\:...\left({iv}\right) \\ $$$$ \\ $$$${we}\:{can}\:{solve}\:{this}\:{only}\:{if}\:\theta\:{or}\:{h}\:{is}\:{given}. \\ $$$${let}'{s}\:{say}\:{h}\:{is}\:{given}. \\ $$$$ \\ $$$${h}−{p}={u}\:\mathrm{sin}\:\theta\:\frac{{a}}{{u}\:\mathrm{cos}\:\theta}−\frac{{g}}{\mathrm{2}}\left(\frac{{a}}{{u}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$${h}−{p}={a}\:\mathrm{tan}\:\theta−\frac{{a}^{\mathrm{2}} {g}}{\mathrm{2}{u}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow\:{h}−{p}={a}\:\mathrm{tan}\:\theta−\frac{{a}^{\mathrm{2}} {g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\:\:\:...\left({v}\right) \\ $$$$ \\ $$$${q}−{h}=\left({u}\:\mathrm{sin}\:\theta−\frac{{ag}}{{u}\:\mathrm{cos}\:\theta}\right)\frac{{a}+{b}}{{eu}\:\mathrm{cos}\:\theta}−\frac{{g}}{\mathrm{2}}\left(\frac{{a}+{b}}{{eu}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$${q}−{h}=\frac{{a}+{b}}{{e}}\:\mathrm{tan}\:\theta−\left({a}+{b}\right)\left(\mathrm{2}{a}+\frac{{a}+{b}}{{e}}\right)\frac{{g}}{\mathrm{2}{eu}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow\:{q}−{h}=\frac{{a}+{b}}{{e}}\:\mathrm{tan}\:\theta−\left({a}+{b}\right)\left(\mathrm{2}{a}+\frac{{a}+{b}}{{e}}\right)\frac{{g}}{\mathrm{2}{eu}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\:\:\:...\left({vi}\right) \\ $$$$ \\ $$$$\left({iv}\right)×{a}^{\mathrm{2}} : \\ $$$$\:{a}^{\mathrm{2}} \left({q}−{h}\right)=\frac{\left({a}+{b}\right){a}^{\mathrm{2}} }{{e}}\:\mathrm{tan}\:\theta−\frac{{a}+{b}}{{e}}\left(\mathrm{2}{a}+\frac{{a}+{b}}{{e}}\right)\left({a}\:\mathrm{tan}\:\theta+{p}−{h}\right) \\ $$$$\:{e}^{\mathrm{2}} {a}^{\mathrm{2}} \left({q}−{h}\right)={ea}^{\mathrm{2}} \left({a}+{b}\right)\:\mathrm{tan}\:\theta−\left({a}+{b}\right)\left(\mathrm{2}{ea}+{a}+{b}\right)\left({a}\:\mathrm{tan}\:\theta+{p}−{h}\right) \\ $$$$\:{a}\left({a}+{b}\right)\left({ea}+{a}+{b}\right)\mathrm{tan}\:\theta=\:{e}^{\mathrm{2}} {a}^{\mathrm{2}} \left({h}−{q}\right)+\left({a}+{b}\right)\left(\mathrm{2}{ea}+{a}+{b}\right)\left({h}−{p}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{{e}^{\mathrm{2}} {a}^{\mathrm{2}} \left({h}−{q}\right)+\left({a}+{b}\right)\left(\mathrm{2}{ea}+{a}+{b}\right)\left({h}−{p}\right)}{{a}\left({a}+{b}\right)\left({ea}+{a}+{b}\right)}=\lambda \\ $$$$ \\ $$$${from}\:\left({v}\right): \\ $$$${u}=\sqrt{\frac{{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right){g}}{\mathrm{2}\left({a}\:\mathrm{tan}\:\theta−{h}+{p}\right)}} \\ $$$$\Rightarrow{u}={a}\sqrt{\frac{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right){g}}{\mathrm{2}\left(\lambda{a}−{h}+{p}\right)}} \\ $$$$ \\ $$$${alternatively}: \\ $$$$\left({v}\right)+\left({vi}\right): \\ $$$${q}−{p}=\left({a}+\frac{{a}+{b}}{{e}}\right)\:\mathrm{tan}\:\theta−\left[{a}^{\mathrm{2}} +\frac{{a}+{b}}{{e}}\left(\mathrm{2}{a}+\frac{{a}+{b}}{{e}}\right)\right]\frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right) \\ $$$${q}−{p}=\left({a}+\frac{{a}+{b}}{{e}}\right)\:\mathrm{tan}\:\theta−\left({a}+\frac{{a}+{b}}{{e}}\right)^{\mathrm{2}} \frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right) \\ $$$${with}\:{A}={a}+\frac{{a}+{b}}{{e}},\:{B}={q}−{p},\:\lambda=\mathrm{tan}\:\theta \\ $$$${we}\:{get} \\ $$$${B}={A}\lambda−{A}^{\mathrm{2}} \left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\frac{{gA}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{1}+\lambda^{\mathrm{2}} }{{A}\lambda−{B}} \\ $$$${let}\:{f}\left(\lambda\right)=\frac{\mathrm{1}+\lambda^{\mathrm{2}} }{{A}\lambda−{B}} \\ $$$$\frac{{df}\left(\lambda\right)}{{d}\lambda}=\frac{\mathrm{2}\lambda}{{A}\lambda−{B}}−\frac{{A}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{\left({A}\lambda−{B}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}+\lambda^{\mathrm{2}} }{{A}\lambda−{B}}=\frac{\mathrm{2}\lambda}{{A}} \\ $$$$\Rightarrow\mathrm{2}\lambda\left({A}\lambda−{B}\right)−{A}\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{A}\lambda^{\mathrm{2}} −\mathrm{2}{B}\lambda−{A}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{B}+\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}{{A}}=\frac{{q}−{p}}{{a}+\frac{{a}+{b}}{{e}}}+\sqrt{\mathrm{1}+\left(\frac{{q}−{p}}{{a}+\frac{{a}+{b}}{{e}}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{u}_{{min}} ^{\mathrm{2}} =\frac{{gA}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{2}\lambda}{{A}}={g}\left({B}+\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{u}_{{min}} =\sqrt{\left[\left({q}−{p}\right)+\sqrt{\left({a}+\frac{{a}+{b}}{{e}}\right)^{\mathrm{2}} +\left({q}−{p}\right)^{\mathrm{2}} }\right]{g}} \\ $$$${h}_{{m}} ={p}+{a}\lambda−\frac{{a}^{\mathrm{2}} {g}}{\mathrm{2}{u}_{{min}} ^{\mathrm{2}} }\left(\mathrm{1}+\lambda^{\mathrm{2}} \right) \\ $$$${h}_{{m}} ={p}+{a}\lambda−\frac{{a}^{\mathrm{2}} \left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{\mathrm{2}{A}\lambda} \\ $$$${h}_{{m}} ={p}+{a}\lambda−\frac{{a}^{\mathrm{2}} \left({A}\lambda−{B}\right)}{{A}^{\mathrm{2}} } \\ $$$${h}_{{m}} ={p}+{a}\left(\mathrm{1}−\frac{{a}}{{A}}\right)\left(\frac{{B}}{{A}}+\frac{\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}{{A}}\right)+\frac{{a}^{\mathrm{2}} {B}}{{A}^{\mathrm{2}} } \\ $$$$\Rightarrow{h}_{{m}} ={p}+{a}\left(\mathrm{1}−\frac{{a}}{{a}+\frac{{a}+{b}}{{e}}}\right)\left[\frac{{q}−{p}}{{a}+\frac{{a}+{b}}{{e}}}+\sqrt{\mathrm{1}+\left(\frac{{q}−{p}}{{a}+\frac{{a}+{b}}{{e}}}\right)^{\mathrm{2}} }\right]+\left(\frac{{a}}{{a}+\frac{{a}+{b}}{{e}}}\right)^{\mathrm{2}} \left({q}−{p}\right) \\ $$$$\theta_{{m}} =\mathrm{tan}^{−\mathrm{1}} \lambda \\ $$$$\Rightarrow\theta_{{m}} =\mathrm{tan}^{−\mathrm{1}} \left[\:\frac{{q}−{p}}{{a}+\frac{{a}+{b}}{{e}}}+\sqrt{\mathrm{1}+\left(\frac{{q}−{p}}{{a}+\frac{{a}+{b}}{{e}}}\right)^{\mathrm{2}} }\right] \\ $$
Commented by MrW3 last updated on 02/Sep/18

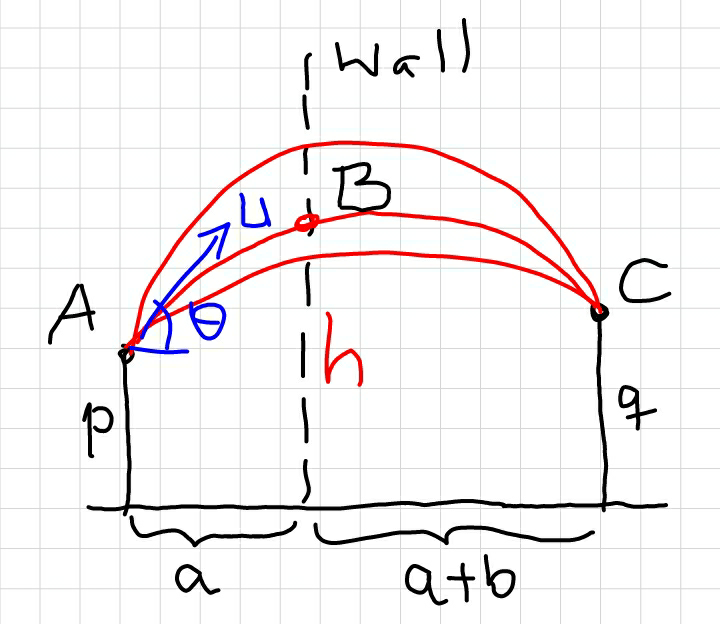
$${let}'{s}\:{assume}\:{the}\:{wall}\:{is}\:``{permeable}'', \\ $$$${the}\:{ball}\:{can}\:{go}\:{through}\:{it}\:{instead}\:{of} \\ $$$${is}\:{reflected}.\:{let}'{s}\:{consider}\:{e}=\mathrm{1}\:\left({see}\:{above}\right).\: \\ $$$${we}\:{can}\:{see}\:{the}\:{ball}\:{has}\:{different}\:{ways}\:{to} \\ $$$${hit}\:{the}\:{wall}\:\left({at}\:{point}\:{B}\right)\:{and}\:{the}\:{point}\:{C}. \\ $$$${i}.{e}.\:{we}\:{can}\:{not}\:{determine}\:{both}\:{h}\:{and}\:{u}. \\ $$$${one}\:{of}\:{them}\:{must}\:{be}\:{given}. \\ $$
Commented by MrW3 last updated on 04/Sep/18

$${and}\:{we}\:{can}\:{see}\:{there}\:{exists}\:{a}\:{point}\:{B} \\ $$$${with}\:{h}={h}_{{m}} \:\:{at}\:{which}\:{the}\:{ball}\:{can}\:{reach} \\ $$$${point}\:{C}\:{with}\:{a}\:{minimal}\:{initial}\:{speed}\:{u}_{{min}} . \\ $$
Commented by MrW3 last updated on 02/Sep/18
Commented by ajfour last updated on 02/Sep/18

$${thank}\:{you}\:{Sir},\:{for}\:{the}\:{effortful} \\ $$$${response};\:{and}\:{correcting}\:{the} \\ $$$${question}\:{even}.\:{I}\:{shall}\:{also}\:\:{try}\:{to} \\ $$$${solve}\:{and}\:{match}\:{my}\:{answer}\:{with} \\ $$$${yours}. \\ $$
Commented by MrW3 last updated on 03/Sep/18

Commented by MrW3 last updated on 03/Sep/18
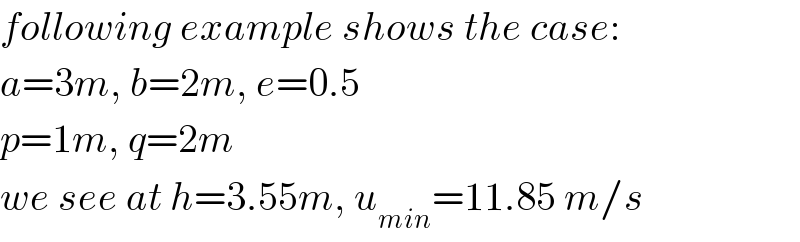
$${following}\:{example}\:{shows}\:{the}\:{case}: \\ $$$${a}=\mathrm{3}{m},\:{b}=\mathrm{2}{m},\:{e}=\mathrm{0}.\mathrm{5} \\ $$$${p}=\mathrm{1}{m},\:{q}=\mathrm{2}{m} \\ $$$${we}\:{see}\:{at}\:{h}=\mathrm{3}.\mathrm{55}{m},\:{u}_{{min}} =\mathrm{11}.\mathrm{85}\:{m}/{s} \\ $$
Commented by ajfour last updated on 03/Sep/18

$$\mathcal{A}{wesome}\:\mathcal{W}{orking}\:{Sir}. \\ $$
Answered by ajfour last updated on 04/Sep/18
![Since the vertical component of u suffers no change upon hitting the wall; q−p = utsin θ−((gt^2 )/2) ...(i) and t = (a/(ucos θ))+((a+b)/(eucos θ)) ...(ii) using (ii) in (i): q−p = usin θ[(a/(ucos θ))+((a+b)/(eucos θ))] −(g/2)[(a/(ucos θ))+((a+b)/(eucos θ))]^2 ⇒ q−p = tan θ(a+((a+b)/e)) −(g/(2u^2 ))(1+tan^2 θ)(a+((a+b)/e))^2 if m=tan θ ; q−p=B ; a+((a+b)/e)=A ((gA^2 )/(2u^2 ))= ((mA−B)/(1+m^2 )) ....(iii) For minimum u ((d(((gA^2 )/(2u^2 ))))/dm)=0 ⇒ A(1+m^2 )=2m(mA−B) or Am^2 −2Bm−A=0 ⇒ m=(B/A)+(√(1+(B^2 /A^2 ))) using this value in eq. (iii) ((gA^2 )/(2u_(min) ^2 )) = ((√(A^2 +B^2 ))/(1+((B/A)+(√(1+(B^2 /A^2 ))) )^2 )) ⇒ u_(min) ^2 =(g/2)×((A^2 +(B+(√(A^2 +B^2 )) )^2 )/(√(A^2 +B^2 ))) u_(min) ^2 = g((√(A^2 +B^2 ))+B) = g[(√((a+((a+b)/e))^2 +(q−p)^2 ))+(q−p)] h=p+am−((a^2 g(1+m^2 ))/(2u_(min) ^2 )) with a=3 , b=2, e=0.5, p=1, q=2 , g=10 , we have u_(min) ^2 = 10[(√(170))+1] u_(min) = (√(140.38)) ≈ 11.85 m/s m=(1/(13))+(√(1+(1/(169)))) =((1+(√(170)))/(13))≈1.08 h= 1+3×1.08−((45×2.16)/(140.38)) ≈ 3.55 m.](Q42842.png)
$${Since}\:{the}\:{vertical}\:{component}\:{of} \\ $$$${u}\:{suffers}\:{no}\:{change}\:{upon}\:{hitting} \\ $$$${the}\:{wall}; \\ $$$$\:{q}−{p}\:=\:{ut}\mathrm{sin}\:\theta−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\:\:\:\:\:\:\:...\left({i}\right) \\ $$$${and}\:\:\:\:\:{t}\:=\:\frac{{a}}{{u}\mathrm{cos}\:\theta}+\frac{{a}+{b}}{{eu}\mathrm{cos}\:\theta}\:\:\:\:...\left({ii}\right) \\ $$$${using}\:\left({ii}\right)\:{in}\:\left({i}\right): \\ $$$${q}−{p}\:=\:{u}\mathrm{sin}\:\theta\left[\frac{{a}}{{u}\mathrm{cos}\:\theta}+\frac{{a}+{b}}{{eu}\mathrm{cos}\:\theta}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{g}}{\mathrm{2}}\left[\frac{{a}}{{u}\mathrm{cos}\:\theta}+\frac{{a}+{b}}{{eu}\mathrm{cos}\:\theta}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\:{q}−{p}\:=\:\mathrm{tan}\:\theta\left({a}+\frac{{a}+{b}}{{e}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta\right)\left({a}+\frac{{a}+{b}}{{e}}\right)^{\mathrm{2}} \\ $$$${if}\:{m}=\mathrm{tan}\:\theta\:;\:{q}−{p}={B}\:;\:{a}+\frac{{a}+{b}}{{e}}={A} \\ $$$$\:\frac{{gA}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }=\:\frac{{mA}−{B}}{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:....\left({iii}\right) \\ $$$${For}\:{minimum}\:\boldsymbol{{u}} \\ $$$$\:\frac{{d}\left(\frac{{gA}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }\right)}{{dm}}=\mathrm{0}\:\:\:\Rightarrow \\ $$$$\:\:{A}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)=\mathrm{2}{m}\left({mA}−{B}\right) \\ $$$${or}\:\:\:{Am}^{\mathrm{2}} −\mathrm{2}{Bm}−{A}=\mathrm{0} \\ $$$$\Rightarrow\:\:{m}=\frac{{B}}{{A}}+\sqrt{\mathrm{1}+\frac{{B}^{\mathrm{2}} }{{A}^{\mathrm{2}} }} \\ $$$${using}\:{this}\:{value}\:{in}\:{eq}.\:\left({iii}\right) \\ $$$$\frac{{gA}^{\mathrm{2}} }{\mathrm{2}{u}_{{min}} ^{\mathrm{2}} }\:=\:\frac{\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{{B}}{{A}}+\sqrt{\mathrm{1}+\frac{{B}^{\mathrm{2}} }{{A}^{\mathrm{2}} }}\:\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:{u}_{{min}} ^{\mathrm{2}} =\frac{{g}}{\mathrm{2}}×\frac{{A}^{\mathrm{2}} +\left({B}+\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\:\right)^{\mathrm{2}} }{\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }} \\ $$$${u}_{{min}} ^{\mathrm{2}} =\:{g}\left(\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }+{B}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:{g}\left[\sqrt{\left({a}+\frac{{a}+{b}}{{e}}\right)^{\mathrm{2}} +\left({q}−{p}\right)^{\mathrm{2}} }+\left({q}−{p}\right)\right] \\ $$$${h}={p}+{am}−\frac{{a}^{\mathrm{2}} {g}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{2}{u}_{{min}} ^{\mathrm{2}} } \\ $$$$ \\ $$$$\:\:\:\:\:\:{with}\:{a}=\mathrm{3}\:,\:{b}=\mathrm{2},\:{e}=\mathrm{0}.\mathrm{5}, \\ $$$$\:\:{p}=\mathrm{1},\:{q}=\mathrm{2}\:,\:{g}=\mathrm{10}\:,\:\:{we}\:{have} \\ $$$$\:{u}_{{min}} ^{\mathrm{2}} =\:\mathrm{10}\left[\sqrt{\mathrm{170}}+\mathrm{1}\right] \\ $$$$\:\:\:{u}_{{min}} =\:\sqrt{\mathrm{140}.\mathrm{38}}\:\approx\:\mathrm{11}.\mathrm{85}\:{m}/{s}\: \\ $$$${m}=\frac{\mathrm{1}}{\mathrm{13}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{169}}}\:=\frac{\mathrm{1}+\sqrt{\mathrm{170}}}{\mathrm{13}}\approx\mathrm{1}.\mathrm{08} \\ $$$${h}=\:\mathrm{1}+\mathrm{3}×\mathrm{1}.\mathrm{08}−\frac{\mathrm{45}×\mathrm{2}.\mathrm{16}}{\mathrm{140}.\mathrm{38}} \\ $$$$\:\:\approx\:\mathrm{3}.\mathrm{55}\:{m}. \\ $$$$ \\ $$
Commented by ajfour last updated on 03/Sep/18
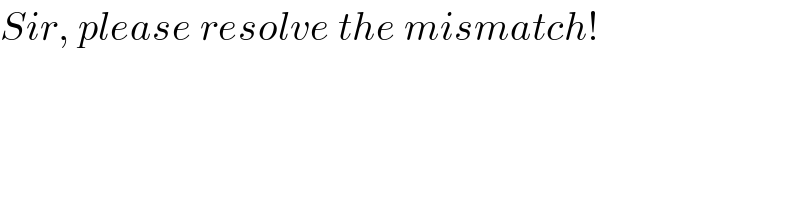
$${Sir},\:{please}\:{resolve}\:{the}\:{mismatch}! \\ $$
Commented by MrW3 last updated on 03/Sep/18
![it can be simplified to: u_(min) ^2 =g(B+(√(A^2 +B^2 ))) u_(min) ^2 =g[(q−p)+(√((a+((a+b)/e))^2 +(q−p)^2 ))] =10×(1+(√(170))) ⇒u_(min) =11.85 m/s I′ll check my working later.](Q42845.png)
$${it}\:{can}\:{be}\:{simplified}\:{to}: \\ $$$${u}_{{min}} ^{\mathrm{2}} ={g}\left({B}+\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\right) \\ $$$${u}_{{min}} ^{\mathrm{2}} ={g}\left[\left({q}−{p}\right)+\sqrt{\left({a}+\frac{{a}+{b}}{{e}}\right)^{\mathrm{2}} +\left({q}−{p}\right)^{\mathrm{2}} }\right] \\ $$$$=\mathrm{10}×\left(\mathrm{1}+\sqrt{\mathrm{170}}\right) \\ $$$$\Rightarrow{u}_{{min}} =\mathrm{11}.\mathrm{85}\:{m}/{s} \\ $$$${I}'{ll}\:{check}\:{my}\:{working}\:{later}. \\ $$
Commented by MrW3 last updated on 04/Sep/18
$${your}\:{solution}\:{is}\:{best}!\:{short}\:{and}\:{clear}. \\ $$
Commented by MrW3 last updated on 03/Sep/18

$${I}\:{found}\:{a}\:{mistake}\:{in}\:{my}\:{working}.\:{it}'{s} \\ $$$${fixed}.\:{now}\:{we}\:{have}\:{the}\:{same}\:{result}. \\ $$
Commented by ajfour last updated on 04/Sep/18
$${thanks}\:{Sir},\:{corrected}. \\ $$
