
Question Number 43486 by ajfour last updated on 11/Sep/18

Commented by ajfour last updated on 11/Sep/18
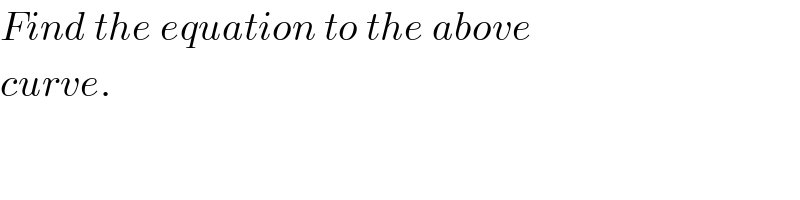
$${Find}\:{the}\:{equation}\:{to}\:{the}\:{above} \\ $$$${curve}. \\ $$
Answered by MJS last updated on 11/Sep/18

$${f}\left({x}\right)={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${f}'\left({x}\right)=\mathrm{4}{ax}^{\mathrm{3}} +\mathrm{3}{bx}^{\mathrm{2}} +\mathrm{2}{cx}+{d} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:{f}\left(−\mathrm{5}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{f}\left(\mathrm{0}\right)=−\mathrm{3}\:\Rightarrow\:{e}=−\mathrm{3} \\ $$$$\left(\mathrm{3}\right)\:\:{f}\left(\mathrm{8}\right)=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\:{f}\left({p}\right)=\mathrm{4} \\ $$$$\left(\mathrm{5}\right)\:\:{f}'\left(−\mathrm{2}\right)=\mathrm{0} \\ $$$$\left(\mathrm{6}\right)\:\:{f}'\left({p}\right)=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{625}{a}−\mathrm{125}{b}+\mathrm{25}{c}−\mathrm{5}{d}−\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:\mathrm{4096}{a}+\mathrm{512}{b}+\mathrm{64}{c}+\mathrm{8}{d}−\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\:{ap}^{\mathrm{4}} +{bp}^{\mathrm{3}} +{cp}^{\mathrm{2}} +{dp}−\mathrm{3}=\mathrm{4} \\ $$$$\left(\mathrm{5}\right)\:\:−\mathrm{32}{a}+\mathrm{12}{b}−\mathrm{4}{c}+{d}=\mathrm{0} \\ $$$$\left(\mathrm{6}\right)\:\:\mathrm{4}{ap}^{\mathrm{3}} +\mathrm{3}{bp}^{\mathrm{2}} +\mathrm{2}{cp}+{d}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:{a}=\frac{{b}}{\mathrm{5}}−\frac{{c}}{\mathrm{25}}+\frac{{d}}{\mathrm{125}}+\frac{\mathrm{3}}{\mathrm{625}} \\ $$$$\left(\mathrm{3}\right)\:\:{b}=\frac{\mathrm{3}{c}}{\mathrm{40}}−\frac{\mathrm{49}{d}}{\mathrm{1600}}−\frac{\mathrm{801}}{\mathrm{64000}} \\ $$$$\left(\mathrm{4}\right)\:\:{c}=\frac{\left(\mathrm{3}{p}−\mathrm{40}\right){d}}{\mathrm{40}{p}}+\frac{\mathrm{147}{p}^{\mathrm{4}} −\mathrm{801}{p}^{\mathrm{3}} −\mathrm{448000}}{\mathrm{1600}{p}^{\mathrm{2}} \left({p}−\mathrm{8}\right)\left({p}+\mathrm{5}\right)} \\ $$$$\left(\mathrm{5}\right)\:\:{d}=\frac{\mathrm{174}{p}^{\mathrm{4}} −\mathrm{729}{p}^{\mathrm{3}} −\mathrm{3579}{p}^{\mathrm{2}} −\mathrm{257600}}{\mathrm{40}{p}\left({p}−\mathrm{8}\right)\left({p}+\mathrm{5}\right)\left(\mathrm{4}{p}+\mathrm{23}\right)} \\ $$$$\left(\mathrm{6}\right)\:\:\frac{\mathrm{21}{p}^{\mathrm{6}} −\mathrm{222}{p}^{\mathrm{5}} −\mathrm{1191}{p}^{\mathrm{4}} +\mathrm{23752}{p}^{\mathrm{3}} +\mathrm{51276}{p}^{\mathrm{2}} −\mathrm{512960}{p}−\mathrm{1030400}}{\mathrm{160}{p}\left({p}−\mathrm{8}\right)\left({p}+\mathrm{5}\right)\left(\mathrm{4}{p}+\mathrm{23}\right)}=\mathrm{0} \\ $$$${p}^{\mathrm{6}} −\frac{\mathrm{74}}{\mathrm{7}}{p}^{\mathrm{5}} −\frac{\mathrm{397}}{\mathrm{7}}{p}^{\mathrm{4}} +\frac{\mathrm{23752}}{\mathrm{21}}{p}^{\mathrm{3}} +\frac{\mathrm{17092}}{\mathrm{7}}{p}^{\mathrm{2}} −\frac{\mathrm{73280}}{\mathrm{3}}{p}−\frac{\mathrm{147200}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{found}\:\mathrm{by}\:\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\frac{\mathrm{147200}}{\mathrm{3}}: \\ $$$${p}_{\mathrm{1}} =−\mathrm{2} \\ $$$${p}^{\mathrm{5}} −\frac{\mathrm{88}}{\mathrm{7}}{p}^{\mathrm{4}} −\frac{\mathrm{221}}{\mathrm{7}}{p}^{\mathrm{3}} +\frac{\mathrm{25078}}{\mathrm{21}}{p}^{\mathrm{2}} +\frac{\mathrm{160}}{\mathrm{3}}{p}−\frac{\mathrm{73600}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{found}\:\mathrm{by}\:\mathrm{approximation}: \\ $$$${p}_{\mathrm{2}} \approx−\mathrm{6}.\mathrm{55745} \\ $$$${p}_{\mathrm{3}} \approx−\mathrm{5}.\mathrm{49542} \\ $$$${p}_{\mathrm{4}} \approx\mathrm{5}.\mathrm{47539} \\ $$$${p}_{\mathrm{5}} ,\:{p}_{\mathrm{6}} \:\notin\mathbb{R} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{4}\:\mathrm{functions} \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{263}}{\mathrm{7200}}{x}^{\mathrm{4}} +\frac{\mathrm{487}}{\mathrm{7200}}{x}^{\mathrm{3}} −\frac{\mathrm{863}}{\mathrm{450}}{x}^{\mathrm{2}} −\frac{\mathrm{2633}}{\mathrm{360}}{x}−\mathrm{3} \\ $$$${f}_{\mathrm{2}} \left({x}\right)=−.\mathrm{0214816}{x}^{\mathrm{4}} −.\mathrm{0918869}{x}^{\mathrm{3}} +\mathrm{1}.\mathrm{40326}{x}^{\mathrm{2}} +\mathrm{6}.\mathrm{02827}{x}−\mathrm{3} \\ $$$${f}_{\mathrm{3}} \left({x}\right)=−.\mathrm{245139}{x}^{\mathrm{4}} −.\mathrm{706945}{x}^{\mathrm{3}} +\mathrm{14}.\mathrm{2076}{x}^{\mathrm{2}} +\mathrm{57}.\mathrm{4695}{x}−\mathrm{3} \\ $$$${f}_{\mathrm{4}} \left({x}\right)=−.\mathrm{000757993}{x}^{\mathrm{4}} −.\mathrm{0348970}{x}^{\mathrm{3}} +.\mathrm{216833}{x}^{\mathrm{2}} +\mathrm{1}.\mathrm{26184}{x}−\mathrm{3} \\ $$
Commented by ajfour last updated on 11/Sep/18
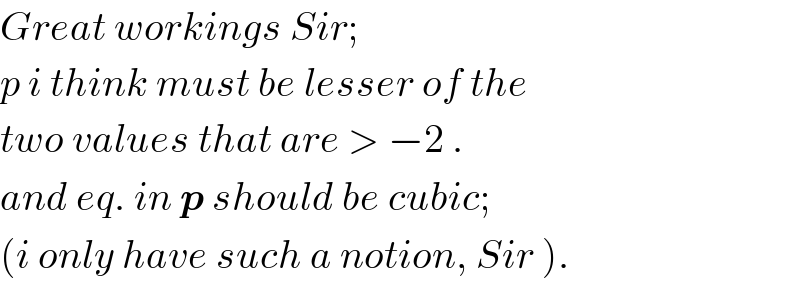
$${Great}\:{workings}\:{Sir}; \\ $$$${p}\:{i}\:{think}\:{must}\:{be}\:{lesser}\:{of}\:{the} \\ $$$${two}\:{values}\:{that}\:{are}\:>\:−\mathrm{2}\:. \\ $$$${and}\:{eq}.\:{in}\:\boldsymbol{{p}}\:{should}\:{be}\:{cubic}; \\ $$$$\left({i}\:{only}\:{have}\:{such}\:{a}\:{notion},\:{Sir}\:\right). \\ $$
Answered by ajfour last updated on 11/Sep/18
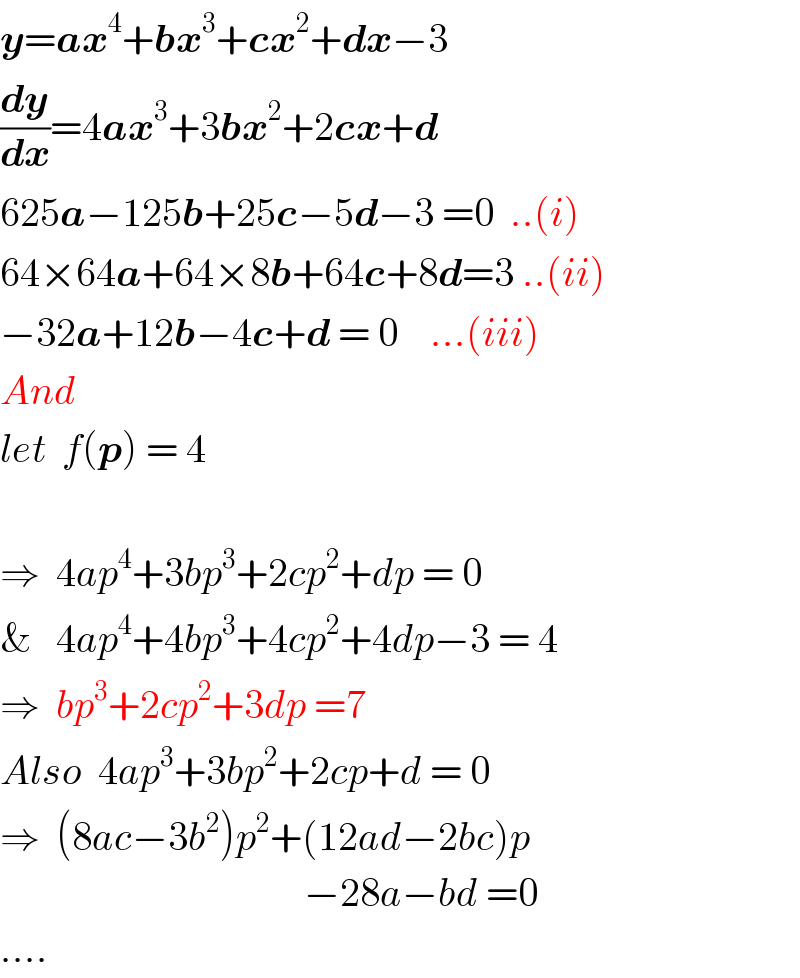
$$\boldsymbol{{y}}=\boldsymbol{{ax}}^{\mathrm{4}} +\boldsymbol{{bx}}^{\mathrm{3}} +\boldsymbol{{cx}}^{\mathrm{2}} +\boldsymbol{{dx}}−\mathrm{3} \\ $$$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\mathrm{4}\boldsymbol{{ax}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{{bx}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{cx}}+\boldsymbol{{d}} \\ $$$$\mathrm{625}\boldsymbol{{a}}−\mathrm{125}\boldsymbol{{b}}+\mathrm{25}\boldsymbol{{c}}−\mathrm{5}\boldsymbol{{d}}−\mathrm{3}\:=\mathrm{0}\:\:..\left({i}\right) \\ $$$$\mathrm{64}×\mathrm{64}\boldsymbol{{a}}+\mathrm{64}×\mathrm{8}\boldsymbol{{b}}+\mathrm{64}\boldsymbol{{c}}+\mathrm{8}\boldsymbol{{d}}=\mathrm{3}\:..\left({ii}\right) \\ $$$$−\mathrm{32}\boldsymbol{{a}}+\mathrm{12}\boldsymbol{{b}}−\mathrm{4}\boldsymbol{{c}}+\boldsymbol{{d}}\:=\:\mathrm{0}\:\:\:\:...\left({iii}\right) \\ $$$${And} \\ $$$${let}\:\:{f}\left(\boldsymbol{{p}}\right)\:=\:\mathrm{4} \\ $$$$ \\ $$$$\Rightarrow\:\:\mathrm{4}{ap}^{\mathrm{4}} +\mathrm{3}{bp}^{\mathrm{3}} +\mathrm{2}{cp}^{\mathrm{2}} +{dp}\:=\:\mathrm{0} \\ $$$$\&\:\:\:\mathrm{4}{ap}^{\mathrm{4}} +\mathrm{4}{bp}^{\mathrm{3}} +\mathrm{4}{cp}^{\mathrm{2}} +\mathrm{4}{dp}−\mathrm{3}\:=\:\mathrm{4} \\ $$$$\Rightarrow\:\:{bp}^{\mathrm{3}} +\mathrm{2}{cp}^{\mathrm{2}} +\mathrm{3}{dp}\:=\mathrm{7} \\ $$$${Also}\:\:\mathrm{4}{ap}^{\mathrm{3}} +\mathrm{3}{bp}^{\mathrm{2}} +\mathrm{2}{cp}+{d}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{8}{ac}−\mathrm{3}{b}^{\mathrm{2}} \right){p}^{\mathrm{2}} +\left(\mathrm{12}{ad}−\mathrm{2}{bc}\right){p} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{28}{a}−{bd}\:=\mathrm{0} \\ $$$$.... \\ $$
Commented by MJS last updated on 11/Sep/18

$$\mathrm{we}\:\mathrm{have}\:\mathrm{got}\:\mathrm{6}\:\mathrm{unknown}\:\mathrm{factors}\:\Rightarrow\:\mathrm{we}\:\mathrm{need} \\ $$$$\mathrm{6}\:\mathrm{equations}. \\ $$$$\mathrm{I}\:\mathrm{went}\:\mathrm{through}\:\mathrm{my}\:\mathrm{work}\:\mathrm{again}\:\mathrm{and}\:\mathrm{found}\:\mathrm{no} \\ $$$$\mathrm{mistake}. \\ $$
Answered by MJS last updated on 11/Sep/18
![trying to get a curve like in your picture f(x)=ax^4 +bx^3 +cx^2 +dx+e f′(x)=4ax^3 +3bx^2 +2cx+d (1) f(−5)=0 (2) f(0)=−3 (3) f(8)=0 (4) f′(−2)=0 solving the system leads to f(x)=ax^4 +((1760a−21)/(640))x^3 −((36640a−111)/(640))x^2 −((18400a−87)/(80))x−3 f(x) must have two zeros in ]0; 8[ f(x)=(x−8)(x+5)(ax^2 +((3680a−21)/(640))x+(3/(40))) x_3 =((21)/(1280a))−((23)/8)−((√((160a−3)(84640a−147)))/(1280a)) x_4 =((21)/(1280a))−((23)/8)+((√((160a−3)(84640a−147)))/(1280a)) ⇒ a<0 ∨ 0<a≤((147)/(84640)) ∨ a≥(3/(160)) 0<x_3 <8 ⇒ a<0 ∨ 0<a≤((147)/(84640)) 0<x_4 <8 ⇒ (3/(1760))≤a≤((147)/(84640)) ⇒ (3/(1760))≤a≤((147)/(84640)) ≈ .00170455≤a≤.00173677 f′(x)=4ax^3 +((3(1760a−21))/(640))x^2 −((36640a−111)/(320))x−((18400a−87)/(80)) f′(x) must have two zeros in ]0; 8[ f′(x)=(x+2)(4ax^2 +((160a−63)/(640))x−((18400a−87)/(160))) x_6 =((63)/(5120a))−(1/(32))−((√(753689600a^2 −3583680a+3969))/(5120a)) x_7 =((63)/(5120a))−(1/(32))+((√(753689600a^2 −3583680a+3969))/(5120a)) ⇒ a<0 ∨ 0<a≤((11199)/(4710560))−((39(√(22)))/(294410)) ∨ a≥((11199)/(4710560))+((39(√(22)))/(294410)) 0<x_6 <8 ⇒ a<0 ∨ 0<a≤((11199)/(4710560))−((39(√(22)))/(294410)) ∨ ((11199)/(4710560))+((39(√(22)))/(294410))≤a≤((87)/(18400)) 0<x_7 <8 ⇒ (3/(1760))≤a≤((11199)/(4710560))−((39(√(22)))/(294410)) ∨ a≥((11199)/(4710560))+((39(√(22)))/(294410)) ⇒ (3/(1760))≤a≤((11199)/(4710560))−((39(√(22)))/(294410)) ∨ ((11199)/(4710560))+((39(√(22)))/(294410))≤a≤((87)/(18400)) ≈ .00170455≤a≤.00175609 ∨ .00299876≤a≤.00472826 ⇒ (3/(1760))≤a≤((147)/(84640)) the local maximum must be 4 f(x_6 )=4 ∨ f(x_7 )=4 f(x_6 )=4 ⇒ a=−.000757993 ∉[(3/(1760)); ((147)/(84640))] f(x_7 )=4 ⇒ no real solution found so we cannot find a solution fitting your picture](Q43499.png)
$$\mathrm{trying}\:\mathrm{to}\:\mathrm{get}\:\mathrm{a}\:\mathrm{curve}\:\mathrm{like}\:\mathrm{in}\:\mathrm{your}\:\mathrm{picture} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${f}'\left({x}\right)=\mathrm{4}{ax}^{\mathrm{3}} +\mathrm{3}{bx}^{\mathrm{2}} +\mathrm{2}{cx}+{d} \\ $$$$\left(\mathrm{1}\right)\:\:{f}\left(−\mathrm{5}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{f}\left(\mathrm{0}\right)=−\mathrm{3} \\ $$$$\left(\mathrm{3}\right)\:\:{f}\left(\mathrm{8}\right)=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\:{f}'\left(−\mathrm{2}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{solving}\:\mathrm{the}\:\mathrm{system}\:\mathrm{leads}\:\mathrm{to} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{4}} +\frac{\mathrm{1760}{a}−\mathrm{21}}{\mathrm{640}}{x}^{\mathrm{3}} −\frac{\mathrm{36640}{a}−\mathrm{111}}{\mathrm{640}}{x}^{\mathrm{2}} −\frac{\mathrm{18400}{a}−\mathrm{87}}{\mathrm{80}}{x}−\mathrm{3} \\ $$$$\left.{f}\left({x}\right)\:\mathrm{must}\:\mathrm{have}\:\mathrm{two}\:\mathrm{zeros}\:\mathrm{in}\:\right]\mathrm{0};\:\mathrm{8}\left[\right. \\ $$$${f}\left({x}\right)=\left({x}−\mathrm{8}\right)\left({x}+\mathrm{5}\right)\left({ax}^{\mathrm{2}} +\frac{\mathrm{3680}{a}−\mathrm{21}}{\mathrm{640}}{x}+\frac{\mathrm{3}}{\mathrm{40}}\right) \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{21}}{\mathrm{1280}{a}}−\frac{\mathrm{23}}{\mathrm{8}}−\frac{\sqrt{\left(\mathrm{160}{a}−\mathrm{3}\right)\left(\mathrm{84640}{a}−\mathrm{147}\right)}}{\mathrm{1280}{a}} \\ $$$${x}_{\mathrm{4}} =\frac{\mathrm{21}}{\mathrm{1280}{a}}−\frac{\mathrm{23}}{\mathrm{8}}+\frac{\sqrt{\left(\mathrm{160}{a}−\mathrm{3}\right)\left(\mathrm{84640}{a}−\mathrm{147}\right)}}{\mathrm{1280}{a}} \\ $$$$\Rightarrow\:{a}<\mathrm{0}\:\vee\:\mathrm{0}<{a}\leqslant\frac{\mathrm{147}}{\mathrm{84640}}\:\vee\:{a}\geqslant\frac{\mathrm{3}}{\mathrm{160}} \\ $$$$\mathrm{0}<{x}_{\mathrm{3}} <\mathrm{8}\:\Rightarrow\:{a}<\mathrm{0}\:\vee\:\mathrm{0}<{a}\leqslant\frac{\mathrm{147}}{\mathrm{84640}} \\ $$$$\mathrm{0}<{x}_{\mathrm{4}} <\mathrm{8}\:\Rightarrow\:\frac{\mathrm{3}}{\mathrm{1760}}\leqslant{a}\leqslant\frac{\mathrm{147}}{\mathrm{84640}} \\ $$$$\Rightarrow\:\frac{\mathrm{3}}{\mathrm{1760}}\leqslant{a}\leqslant\frac{\mathrm{147}}{\mathrm{84640}}\:\approx\:.\mathrm{00170455}\leqslant{a}\leqslant.\mathrm{00173677} \\ $$$$ \\ $$$${f}'\left({x}\right)=\mathrm{4}{ax}^{\mathrm{3}} +\frac{\mathrm{3}\left(\mathrm{1760}{a}−\mathrm{21}\right)}{\mathrm{640}}{x}^{\mathrm{2}} −\frac{\mathrm{36640}{a}−\mathrm{111}}{\mathrm{320}}{x}−\frac{\mathrm{18400}{a}−\mathrm{87}}{\mathrm{80}} \\ $$$$\left.{f}'\left({x}\right)\:\mathrm{must}\:\mathrm{have}\:\mathrm{two}\:\mathrm{zeros}\:\mathrm{in}\:\right]\mathrm{0};\:\mathrm{8}\left[\right. \\ $$$${f}'\left({x}\right)=\left({x}+\mathrm{2}\right)\left(\mathrm{4}{ax}^{\mathrm{2}} +\frac{\mathrm{160}{a}−\mathrm{63}}{\mathrm{640}}{x}−\frac{\mathrm{18400}{a}−\mathrm{87}}{\mathrm{160}}\right) \\ $$$${x}_{\mathrm{6}} =\frac{\mathrm{63}}{\mathrm{5120}{a}}−\frac{\mathrm{1}}{\mathrm{32}}−\frac{\sqrt{\mathrm{753689600}{a}^{\mathrm{2}} −\mathrm{3583680}{a}+\mathrm{3969}}}{\mathrm{5120}{a}} \\ $$$${x}_{\mathrm{7}} =\frac{\mathrm{63}}{\mathrm{5120}{a}}−\frac{\mathrm{1}}{\mathrm{32}}+\frac{\sqrt{\mathrm{753689600}{a}^{\mathrm{2}} −\mathrm{3583680}{a}+\mathrm{3969}}}{\mathrm{5120}{a}} \\ $$$$\Rightarrow\:{a}<\mathrm{0}\:\vee\:\mathrm{0}<{a}\leqslant\frac{\mathrm{11199}}{\mathrm{4710560}}−\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}}\:\vee\:{a}\geqslant\frac{\mathrm{11199}}{\mathrm{4710560}}+\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}} \\ $$$$\mathrm{0}<{x}_{\mathrm{6}} <\mathrm{8}\:\Rightarrow\:{a}<\mathrm{0}\:\vee\:\mathrm{0}<{a}\leqslant\frac{\mathrm{11199}}{\mathrm{4710560}}−\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}}\:\vee\:\frac{\mathrm{11199}}{\mathrm{4710560}}+\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}}\leqslant{a}\leqslant\frac{\mathrm{87}}{\mathrm{18400}} \\ $$$$\mathrm{0}<{x}_{\mathrm{7}} <\mathrm{8}\:\Rightarrow\:\frac{\mathrm{3}}{\mathrm{1760}}\leqslant{a}\leqslant\frac{\mathrm{11199}}{\mathrm{4710560}}−\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}}\:\vee\:{a}\geqslant\frac{\mathrm{11199}}{\mathrm{4710560}}+\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}} \\ $$$$\Rightarrow\:\frac{\mathrm{3}}{\mathrm{1760}}\leqslant{a}\leqslant\frac{\mathrm{11199}}{\mathrm{4710560}}−\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}}\:\vee\:\frac{\mathrm{11199}}{\mathrm{4710560}}+\frac{\mathrm{39}\sqrt{\mathrm{22}}}{\mathrm{294410}}\leqslant{a}\leqslant\frac{\mathrm{87}}{\mathrm{18400}} \\ $$$$\approx\:.\mathrm{00170455}\leqslant{a}\leqslant.\mathrm{00175609}\:\vee\:.\mathrm{00299876}\leqslant{a}\leqslant.\mathrm{00472826} \\ $$$$\Rightarrow\:\frac{\mathrm{3}}{\mathrm{1760}}\leqslant{a}\leqslant\frac{\mathrm{147}}{\mathrm{84640}} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{local}\:\mathrm{maximum}\:\mathrm{must}\:\mathrm{be}\:\mathrm{4} \\ $$$${f}\left({x}_{\mathrm{6}} \right)=\mathrm{4}\:\vee\:{f}\left({x}_{\mathrm{7}} \right)=\mathrm{4} \\ $$$${f}\left({x}_{\mathrm{6}} \right)=\mathrm{4}\:\Rightarrow\:{a}=−.\mathrm{000757993}\:\notin\left[\frac{\mathrm{3}}{\mathrm{1760}};\:\frac{\mathrm{147}}{\mathrm{84640}}\right] \\ $$$${f}\left({x}_{\mathrm{7}} \right)=\mathrm{4}\:\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{found} \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{fitting}\:\mathrm{your}\:\mathrm{picture} \\ $$
Commented by ajfour last updated on 11/Sep/18

$${Very}\:{unfortunate}\:{Sir},\:{i}\:{shall}\:{be} \\ $$$${more}\:{careful}\:{in}\:{creating}\:{questions}. \\ $$
Commented by MJS last updated on 11/Sep/18
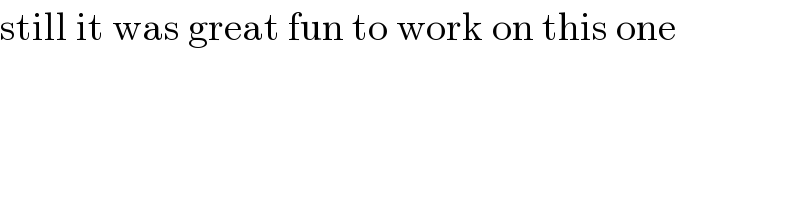
$$\mathrm{still}\:\mathrm{it}\:\mathrm{was}\:\mathrm{great}\:\mathrm{fun}\:\mathrm{to}\:\mathrm{work}\:\mathrm{on}\:\mathrm{this}\:\mathrm{one} \\ $$
