
Question Number 44497 by MrW3 last updated on 30/Sep/18
Commented by ajfour last updated on 30/Sep/18
$${the}\:{concept}\:{of}\:{greater}\:{circle} \\ $$$${route}\:{has}\:{use}\:{in}\:{this},\:{i}\:{am}\:{not} \\ $$$${able}\:{to}\:{apply}\:{it}\:{yet}.. \\ $$
Commented by MrW3 last updated on 30/Sep/18

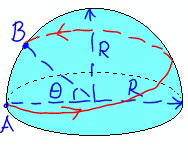
$${A}\:{mountain}\:{has}\:{the}\:{shape}\:{of}\:{semi} \\ $$$${sphere}.\:{From}\:{point}\:{A}\:{at}\:{the}\:{foot}\:{of} \\ $$$${the}\:{mountain}\:{to}\:{point}\:{B}\:{over}\:{point}\:{A} \\ $$$${a}\:{sightseeing}\:{path}\:{around}\:{the}\:{mountain} \\ $$$${is}\:{to}\:{be}\:{built}.\:{Find}\:{the}\:{shortes}\:{length} \\ $$$${of}\:{the}\:{path}\:{in}\:{terms}\:{of}\:{R}\:{and}\:\theta. \\ $$
Commented by MrW3 last updated on 30/Sep/18

Commented by MrW3 last updated on 30/Sep/18

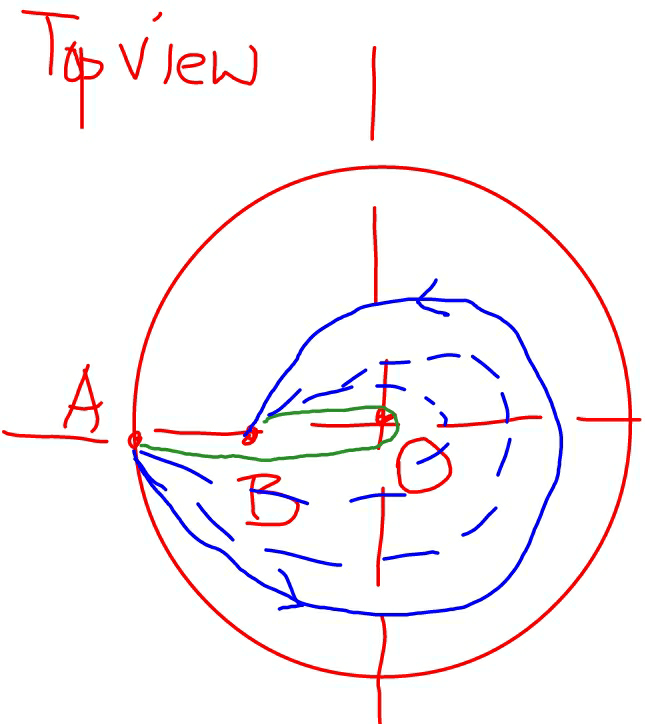
$${I}\:{created}\:{this}\:{question}\:{by}\:{myself}\:{and} \\ $$$${have}\:{no}\:{solution}\:{in}\:{mind}.\:{It}\:{is}\:{true} \\ $$$${that}\:{the}\:{shortest}\:{distance}\:{between}\:{two} \\ $$$${points}\:{on}\:{the}\:{sphere}\:{surface}\:{is}\:{the} \\ $$$${path}\:{through}\:{the}\:{great}\:{circle}.\:{As}\:{the} \\ $$$${following}\:{picture}\:{shows}\:{all}\:{blue}\:{pathes} \\ $$$${fulfill}\:{the}\:{requirement}.\:{so}\:{the}\:{green} \\ $$$${one}\:{is}\:{the}\:{shortes}\:{one}.\:{then}\:{we}\:{have} \\ $$$${L}_{{min}} =\left(\pi−\theta\right){R} \\ $$
Commented by MrW3 last updated on 30/Sep/18
Commented by MJS last updated on 01/Oct/18

$$\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{is}\:\mathrm{along}\:\mathrm{the}\:\mathrm{greatest} \\ $$$$\mathrm{circle}\:\mathrm{through}\:{A}\:\mathrm{and}\:{B},\:\mathrm{all}\:\mathrm{routes}\:\mathrm{around}\:\mathrm{the} \\ $$$$\mathrm{sphere}\:\mathrm{are}\:\mathrm{longer},\:\mathrm{so}\:\mathrm{we}\:\mathrm{need}\:\mathrm{another}\:\mathrm{criteria} \\ $$$$ \\ $$$$\mathrm{btw}.\:\mathrm{a}\:\mathrm{sumilar}\:\mathrm{issue}\:\mathrm{occurs}\:\mathrm{at}\:\mathrm{the}\:\mathrm{former} \\ $$$$\mathrm{problem}\:\mathrm{with}\:\mathrm{the}\:\mathrm{cone}−\mathrm{mountain}\:\mathrm{with} \\ $$$$\mathrm{opening}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cone}\:\geqslant\:\mathrm{60}° \\ $$$$\mathrm{the}\:\mathrm{train}\:\mathrm{cannot}\:\mathrm{follow}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{along} \\ $$$$\mathrm{the}\:\mathrm{lateral}\:\mathrm{surface}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cone} \\ $$
Commented by MrW3 last updated on 01/Oct/18
$${thanks}\:{for}\:{this}\:{new}\:{aspect}! \\ $$
Commented by MJS last updated on 01/Oct/18

$$\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{approximate}\:\mathrm{the}\:\mathrm{half}\:\mathrm{sphere}\:\mathrm{with} \\ $$$$\mathrm{cones},\:\mathrm{and}\:\mathrm{found}\:\mathrm{the}\:\mathrm{mentioned}\:\mathrm{problem}. \\ $$
