
Question Number 44584 by Joel578 last updated on 01/Oct/18
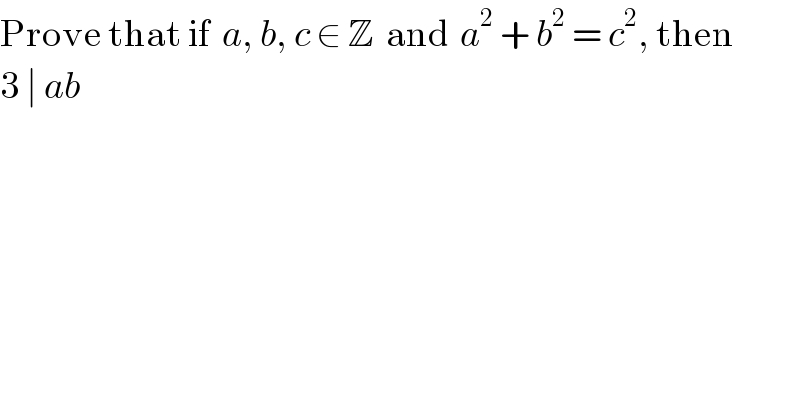
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{if}\:\:{a},\:{b},\:{c}\:\in\:\mathbb{Z}\:\:\mathrm{and}\:\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:=\:{c}^{\mathrm{2}} ,\:\mathrm{then} \\ $$$$\mathrm{3}\:\mid\:{ab} \\ $$
Commented by ajfour last updated on 02/Oct/18

$${then}\:\:\mathrm{3}\mid{ab}\:\:\:{means}\:?!.. \\ $$
Commented by rahul 19 last updated on 02/Oct/18
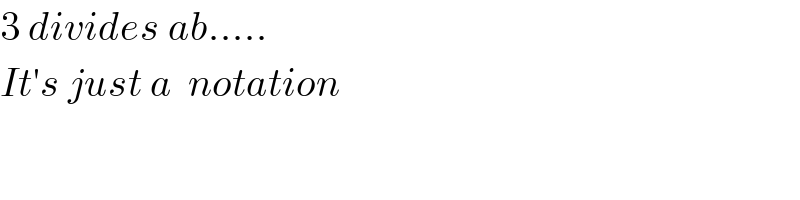
$$\mathrm{3}\:{divides}\:{ab}..... \\ $$$${It}'{s}\:{just}\:{a}\:\:{notation} \\ $$
Commented by ajfour last updated on 02/Oct/18

$${thanks}\:{rahul}. \\ $$
Commented by Joel578 last updated on 03/Oct/18

$$\mathrm{Yes},\:\mathrm{3}\:\mid\:{ab}\:\mathrm{means}\:\mathrm{there}\:\mathrm{is}\:\mathrm{such}\:\mathrm{number}\:{x}\:\mathrm{that}\: \\ $$$$\mathrm{satisfy}\:{ab}\:=\:\mathrm{3}{x} \\ $$
Commented by Joel578 last updated on 03/Oct/18

$$\mathrm{I}'\mathrm{m}\:\mathrm{having}\:\mathrm{trouble}\:\mathrm{how}\:\mathrm{to}\:\mathrm{start}\:\mathrm{the}\:\mathrm{proof} \\ $$
Answered by arcana last updated on 03/Oct/18

$$\mathrm{podemos}\:\mathrm{ver}\:\mathrm{solamente}\:\mathrm{para}\:\mathrm{el}\:\mathrm{caso} \\ $$$$\mathrm{de}\:\mathrm{que}\:{a},{b},{c}\:\:\mathrm{sea}\:\mathrm{una}\:{solucion}\:{primitiva}, \\ $$$$\mathrm{es}\:\mathrm{decir}\:\left({a},{b},{c}\right)=\mathrm{1},\:\mathrm{ya}\:\mathrm{que}\:\mathrm{las}\:\mathrm{soluciones}\:\mathrm{primitivas} \\ $$$$\mathrm{pueden}\:\mathrm{generar}\:\mathrm{los}\:\mathrm{demas}\:\mathrm{casos}. \\ $$$${A}\mathrm{hora}\:\mathrm{solo}\:\mathrm{uno}\:\mathrm{de}\:\mathrm{los}\:\mathrm{enteros}\:{a},{b}\:\mathrm{debe} \\ $$$$\mathrm{ser}\:\mathrm{impar},\:\mathrm{pues}\:\mathrm{si}\:\mathrm{los}\:\mathrm{lo}\:\mathrm{son}\:{entonces}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\mathrm{es} \\ $$$$\mathrm{de}\:\mathrm{la}\:\mathrm{forma}\:\mathrm{4}{k}+\mathrm{2}\:\mathrm{pero}\:\mathrm{todo}\:\mathrm{cuadrado} \\ $$$$\mathrm{perfecto}\:\mathrm{es}\:\mathrm{de}\:\mathrm{la}\:\mathrm{forma}\:\mathrm{4}{k}\:{o}\:\mathrm{4}{k}+\mathrm{1}\:\left(\rightarrow\leftarrow\right). \\ $$$$ \\ $$$${B}\mathrm{ajo}\:\mathrm{estas}\:\mathrm{condiciones}\:\mathrm{podemos}\:\mathrm{usar}\:\mathrm{el} \\ $$$$\mathrm{siguiente}\:\boldsymbol{\mathrm{teorema}}: \\ $$$$ \\ $$$${S}\mathrm{i}\:{a},{b},{c}\:\in\mathbb{Z}\:{es}\:{una}\:{solucion}\:{primitiva} \\ $$$${donde}\:{a}\:{es}\:{impar}\:{para}\:{la}\:{ecuacion} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \:{sii}\:{existen}\:{enteros}\:{x},{y} \\ $$$${tales}\:{que}: \\ $$$${a}={x}^{\mathrm{2}} −{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{c}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${b}=\mathrm{2}{xy} \\ $$$$ \\ $$$${con}\:\left({x},{y}\right)=\mathrm{1},\:{x}>{y},\:{x}\:{e}\:{y}\:{tienen}\:{distinta} \\ $$$${paridad}. \\ $$$${por}\:{lo}\:{anterior}\:\:{tenemos}\:{ab}=\mathrm{2}{xy}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right). \\ $$$${y}\:{esto}\:{se}\:{reduce}\:{en}\:{ver}\:{si}\:\mathrm{3}\mid{x}\:\vee\:\mathrm{3}\mid{y}\:\vee \\ $$$$\mathrm{3}\mid\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right). \\ $$$$ \\ $$$${si}\:\mathrm{3}\mid{x}\:\vee\:\mathrm{3}\mid{y}\:{entoncea}\:{esta}\:{hecho}. \\ $$$${si}\:\mathrm{3}\:{no}\:{divide}\:{a}\:{x}\:{ni}\:{y}\:,\:{entonces} \\ $$$${x},{y}\:{son}\:{de}\:{la}\:{forma}\:\mathrm{3}{k}+\mathrm{1}\:{o}\:\mathrm{3}{k}+\mathrm{2},\:{k}\:{entero} \\ $$$${para}\:{k}_{\mathrm{0}} ,{k}_{\mathrm{1}} \in\mathbb{Z} \\ $$$${caso}\:\mathrm{1}:\:\:{si}\:{x}=\mathrm{3}{k}_{\mathrm{0}} +\mathrm{1},\:{y}=\mathrm{3}{k}_{\mathrm{1}} +\mathrm{1} \\ $$$$ \\ $$$${luego}\:\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{3}\left(\mathrm{3}{k}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{k}_{\mathrm{0}} −\mathrm{3}{k}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{k}_{\mathrm{1}} \right) \\ $$$${esto}\:{es}\:\mathrm{3}\mid\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\Rightarrow\mathrm{3}\mid{ab} \\ $$$$ \\ $$$${caso}\:\mathrm{2}:\:\:{si}\:{x}=\mathrm{3}{k}_{\mathrm{0}} +\mathrm{1},\:{y}=\mathrm{3}{k}_{\mathrm{1}} +\mathrm{2} \\ $$$$ \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{3}\left(\mathrm{3}{k}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{k}_{\mathrm{0}} −\mathrm{3}{k}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{k}_{\mathrm{1}} −\mathrm{1}\right) \\ $$$${luego}\:\:\mathrm{3}\mid\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\Rightarrow\mathrm{3}\mid{ab} \\ $$$$ \\ $$$${caso}\:\mathrm{3}:\:{si}\:{x}=\mathrm{3}{k}_{\mathrm{0}} +\mathrm{2},\:{y}=\mathrm{3}{k}_{\mathrm{1}} +\mathrm{1} \\ $$$${es}\:{similar}\:{al}\:{caso}\:\mathrm{2} \\ $$$${caso}\:\mathrm{4}:\:{si}\:{x}=\mathrm{3}{k}_{\mathrm{0}} +\mathrm{2},\:{y}=\mathrm{3}{k}_{\mathrm{1}} +\mathrm{2} \\ $$$${similar}\:{al}\:{caso}\:\mathrm{1}. \\ $$$$ \\ $$$$\mathrm{La}\:\mathrm{demostracion}\:\mathrm{del}\:\mathrm{teorema}\:\mathrm{se}\:\mathrm{puede}\:\mathrm{encontrar}\:\mathrm{en}\:\mathrm{el}\:\mathrm{libro}:\:\mathrm{teoria}\:\mathrm{de}\:\mathrm{numeros}, \\ $$$$\mathrm{Rubiano} \\ $$
