
Question Number 46182 by Meritguide1234 last updated on 22/Oct/18
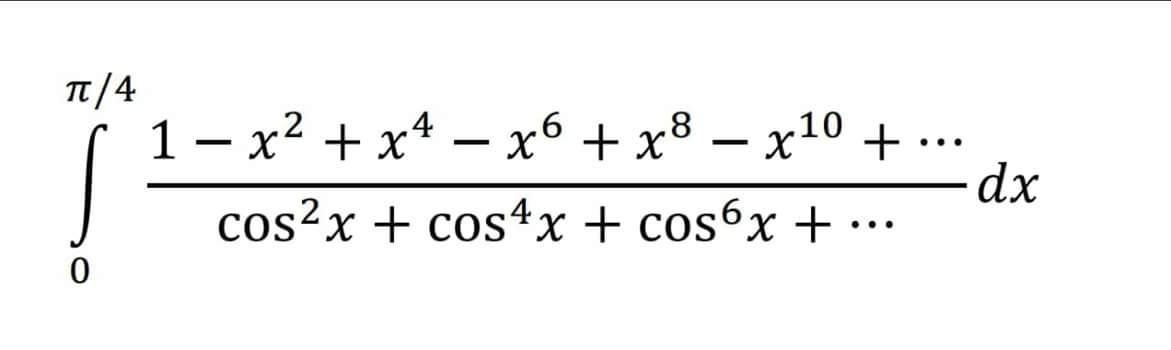
Commented by maxmathsup by imad last updated on 22/Oct/18
![we have 1−x^2 +x^4 −....=Σ_(n=0) ^∞ (−x^2 )^n =(1/(1+x^2 )) and cos^2 x +cos^4 x +cos^6 x +...=cos^2 x(1+cos^2 x +cos^4 x +....) =cos^2 x{(1/(1−cos^2 x))}=(1/(tan^2 x)) ⇒ I = ∫_0 ^(π/4) ((tan^2 x)/(1+x^2 ))dx by parts I =∫_0 ^(π/4) tan^2 x(Σ_(n=0) ^∞ (−1)^n x^n )ex =Σ_(n=0) ^∞ (−1)^n ∫_0 ^(π/4) x^n tan^2 x dt =Σ_(n=0) ^∞ (−1)^n A_n with A_n =∫_0 ^(π/4) x^n tan^2 x dx by parts A_n =[(1/(n+1)) x^(n+1) tan^2 x]_0 ^(π/4) −∫_0 ^(π/4) (x^(n+1) /(n+1)) (2tanx)(1+tan^2 x)dx =(1/(n+1))((π/4))^(n+1) −(2/(n+1)) ∫_0 ^(π/4) x^(n+1) tanx dx −(2/(n+1)) ∫_0 ^(π/4) x^(n+1) tan^3 t dt...be continued...](Q46217.png)
$$\:{we}\:{have}\:\mathrm{1}−{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} −....=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−{x}^{\mathrm{2}} \right)^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{and} \\ $$$${cos}^{\mathrm{2}} {x}\:\:+{cos}^{\mathrm{4}} {x}\:+{cos}^{\mathrm{6}} {x}\:+...={cos}^{\mathrm{2}} {x}\left(\mathrm{1}+{cos}^{\mathrm{2}} {x}\:+{cos}^{\mathrm{4}} {x}\:+....\right) \\ $$$$={cos}^{\mathrm{2}} {x}\left\{\frac{\mathrm{1}}{\mathrm{1}−{cos}^{\mathrm{2}} {x}}\right\}=\frac{\mathrm{1}}{{tan}^{\mathrm{2}} {x}}\:\Rightarrow\:{I}\:=\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{by}\:{parts}\: \\ $$$$\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:{tan}^{\mathrm{2}} {x}\left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \right){ex}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{x}^{{n}} \:{tan}^{\mathrm{2}} {x}\:{dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{A}_{{n}} \:\:{with}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{x}^{{n}} \:{tan}^{\mathrm{2}} {x}\:{dx}\:\:{by}\:{parts}\: \\ $$$${A}_{{n}} =\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} {tan}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:\left(\mathrm{2}{tanx}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\frac{\pi}{\mathrm{4}}\right)^{{n}+\mathrm{1}} \:\:−\frac{\mathrm{2}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{x}^{{n}+\mathrm{1}} {tanx}\:{dx}\:−\frac{\mathrm{2}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{{n}+\mathrm{1}} {tan}^{\mathrm{3}} {t}\:{dt}...{be}\:{continued}... \\ $$
Commented by maxmathsup by imad last updated on 22/Oct/18
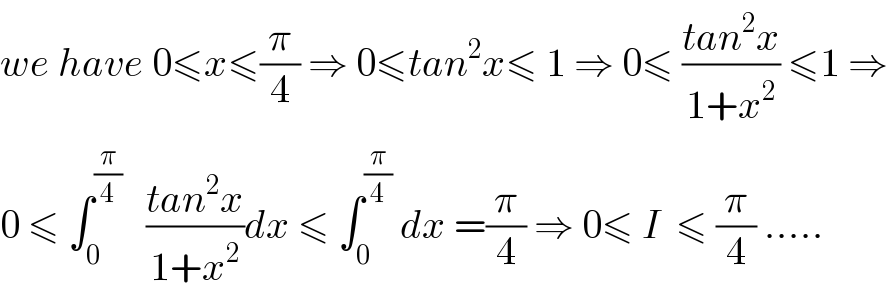
$${we}\:{have}\:\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{4}}\:\Rightarrow\:\mathrm{0}\leqslant{tan}^{\mathrm{2}} {x}\leqslant\:\mathrm{1}\:\Rightarrow\:\mathrm{0}\leqslant\:\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\leqslant\mathrm{1}\:\Rightarrow\: \\ $$$$\mathrm{0}\:\leqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\leqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{dx}\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow\:\mathrm{0}\leqslant\:{I}\:\:\leqslant\:\frac{\pi}{\mathrm{4}}\:..... \\ $$
Commented by Meritguide1234 last updated on 22/Oct/18

$${very}\:{good} \\ $$
Commented by maxmathsup by imad last updated on 22/Oct/18

$${thank}\:{you}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Oct/18
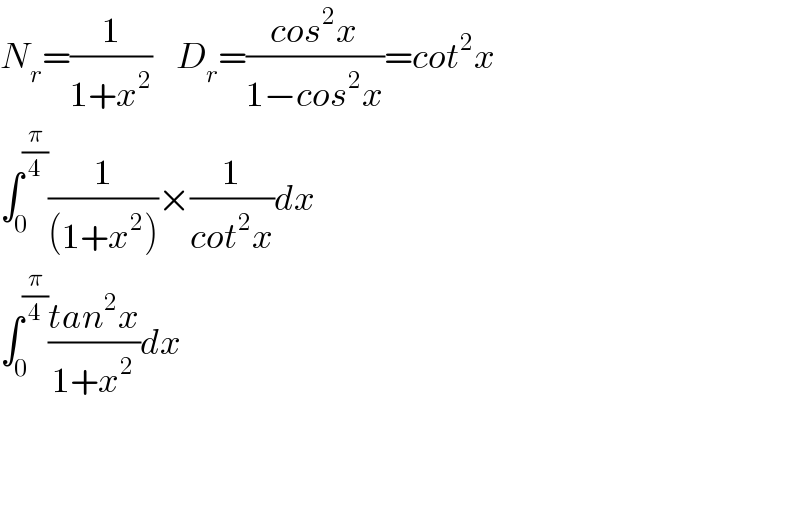
$${N}_{{r}} =\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:\:{D}_{{r}} =\frac{{cos}^{\mathrm{2}} {x}}{\mathrm{1}−{cos}^{\mathrm{2}} {x}}={cot}^{\mathrm{2}} {x} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}×\frac{\mathrm{1}}{{cot}^{\mathrm{2}} {x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Oct/18
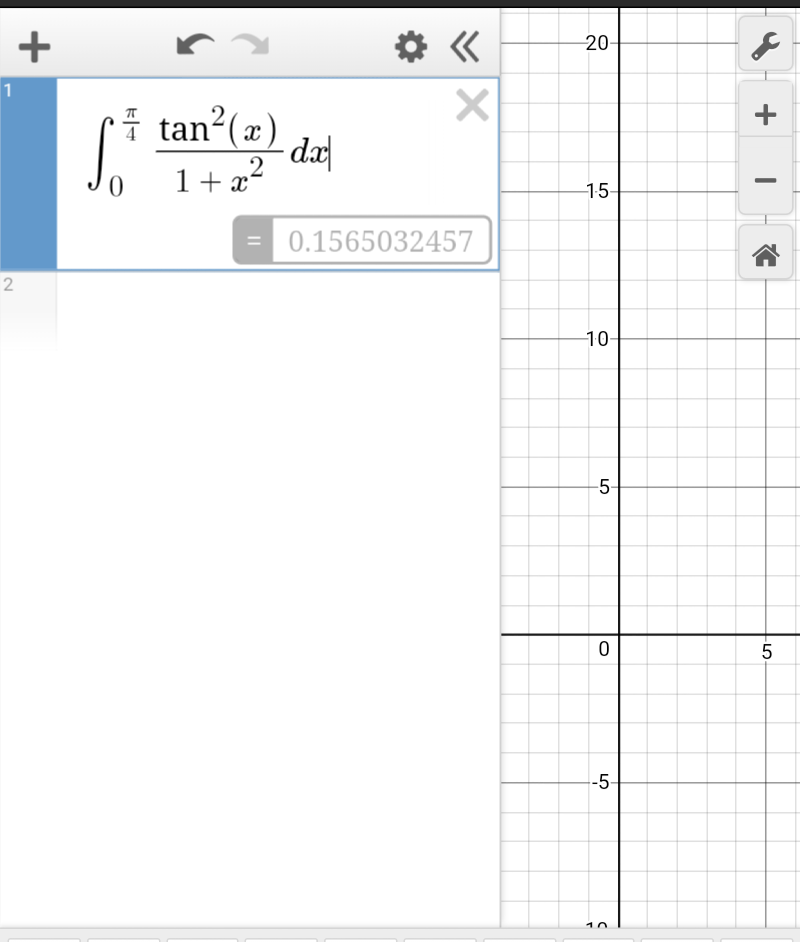
Commented by Meritguide1234 last updated on 22/Oct/18
$${need}\:{more}\:{specific}\:... \\ $$
