Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 46453 by MrW3 last updated on 26/Oct/18

Commented by MrW3 last updated on 27/Oct/18

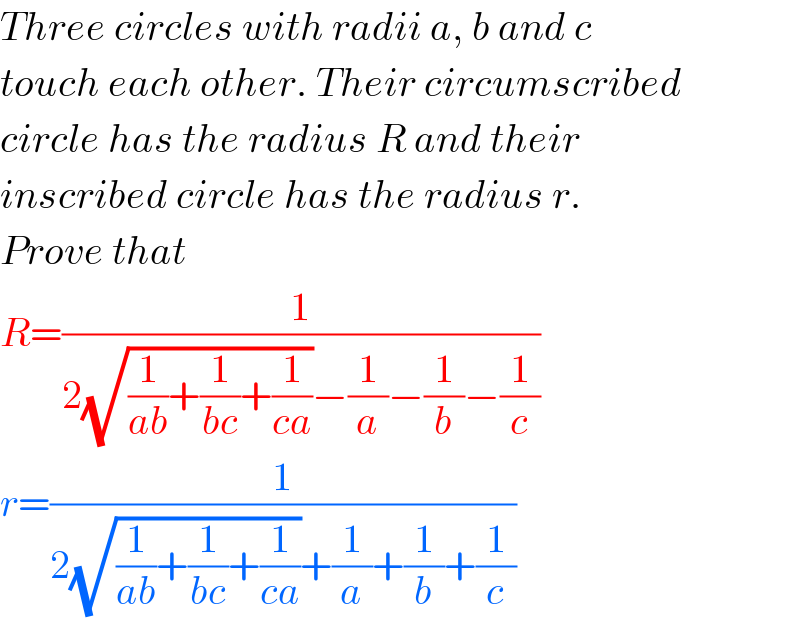
Three circles with radii a, b and c touch each other. Their circumscribed circle has the radius R and their inscribed circle has the radius r. Prove that R=(1/(2(√((1/(ab))+(1/(bc))+(1/(ca))))−(1/a)−(1/b)−(1/c))) r=(1/(2(√((1/(ab))+(1/(bc))+(1/(ca))))+(1/a)+(1/b)+(1/c)))

$${Three}\:{circles}\:{with}\:{radii}\:{a},\:{b}\:{and}\:{c} \\ $$$${touch}\:{each}\:{other}.\:{Their}\:{circumscribed} \\ $$$${circle}\:{has}\:{the}\:{radius}\:{R}\:{and}\:{their} \\ $$$${inscribed}\:{circle}\:{has}\:{the}\:{radius}\:{r}. \\ $$$${Prove}\:{that} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}−\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{b}}−\frac{\mathrm{1}}{{c}}} \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}} \\ $$

Commented by behi83417@gmail.com last updated on 26/Oct/18

vety beautiful question!

$${vety}\:{beautiful}\:{question}! \\ $$

Commented by MJS last updated on 26/Oct/18

this is related to a former question, couldn′t find it right now. the inscribed circle always exists but the circumcircle sometimes degenerates to a common tangent or even a circle touching the 3 given from outside (imagine 2 big circles and the 3^(rd) one small enough to fit in the “gap” between them)

$$\mathrm{this}\:\mathrm{is}\:\mathrm{related}\:\mathrm{to}\:\mathrm{a}\:\mathrm{former}\:\mathrm{question},\:\mathrm{couldn}'\mathrm{t} \\ $$$$\mathrm{find}\:\mathrm{it}\:\mathrm{right}\:\mathrm{now}. \\ $$$$\mathrm{the}\:\mathrm{inscribed}\:\mathrm{circle}\:\mathrm{always}\:\mathrm{exists}\:\mathrm{but}\:\mathrm{the} \\ $$$$\mathrm{circumcircle}\:\mathrm{sometimes}\:\mathrm{degenerates}\:\mathrm{to}\:\mathrm{a} \\ $$$$\mathrm{common}\:\mathrm{tangent}\:\mathrm{or}\:\mathrm{even}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{touching} \\ $$$$\mathrm{the}\:\mathrm{3}\:\mathrm{given}\:\mathrm{from}\:\mathrm{outside}\:\left(\mathrm{imagine}\:\mathrm{2}\:\mathrm{big}\:\mathrm{circles}\right. \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{one}\:\mathrm{small}\:\mathrm{enough}\:\mathrm{to}\:\mathrm{fit}\:\mathrm{in}\:\mathrm{the} \\ $$$$\left.``\mathrm{gap}''\:\mathrm{between}\:\mathrm{them}\right) \\ $$

Commented by MJS last updated on 26/Oct/18

I once downloaded my solution as an image, here it is (sorry can′t change it so it doesn′t fit exactly here but it might help)

$$\mathrm{I}\:\mathrm{once}\:\mathrm{downloaded}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{as}\:\mathrm{an}\:\mathrm{image},\: \\ $$$$\mathrm{here}\:\mathrm{it}\:\mathrm{is}\:\left(\mathrm{sorry}\:\mathrm{can}'\mathrm{t}\:\mathrm{change}\:\mathrm{it}\:\mathrm{so}\:\mathrm{it}\:\mathrm{doesn}'\mathrm{t}\right. \\ $$$$\left.\mathrm{fit}\:\mathrm{exactly}\:\mathrm{here}\:\mathrm{but}\:\mathrm{it}\:\mathrm{might}\:\mathrm{help}\right) \\ $$

Commented by MJS last updated on 26/Oct/18

Commented by MrW3 last updated on 26/Oct/18

This question is indeed derived from the question #37209 from ajfour sir. The given formulas for R and r are simple, but not easy to prove. Can we find an easy way for the proof?

$${This}\:{question}\:{is}\:{indeed}\:{derived}\:{from} \\ $$$${the}\:{question}\:#\mathrm{37209}\:{from}\:{ajfour}\:{sir}. \\ $$$${The}\:{given}\:{formulas}\:{for}\:{R}\:{and}\:{r}\:{are} \\ $$$${simple},\:{but}\:{not}\:{easy}\:{to}\:{prove}.\:{Can}\:{we} \\ $$$${find}\:{an}\:{easy}\:{way}\:{for}\:{the}\:{proof}? \\ $$

Answered by ajfour last updated on 27/Oct/18

Σ(√(R[R−(a+b)]ab))=(√((a+b+c)abc)) cant solve for R !

$$\Sigma\sqrt{{R}\left[{R}−\left({a}+{b}\right)\right]{ab}}=\sqrt{\left({a}+{b}+{c}\right){abc}} \\ $$$${cant}\:{solve}\:{for}\:{R}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com