
Question Number 46611 by ajfour last updated on 29/Oct/18
Commented by ajfour last updated on 29/Oct/18

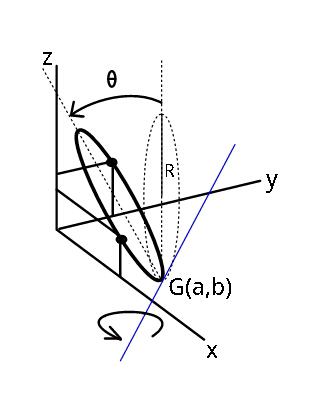
$${A}\:{ring}\:{of}\:{radius}\:{R}\:{stands}\:{upright} \\ $$$${at}\:{G}\left({a},{b},\mathrm{0}\right).\:{Along}\:{which}\:{line},\:{in} \\ $$$${xy}-{plane}\:{and}\:{passing}\:{through}\:{G}, \\ $$$${as}\:{axis}\:{should}\:{the}\:{ring}\:{be}\:{tilted} \\ $$$${and}\:{by}\:{how}\:{much}\:\left(\theta\right)\:{such}\:{that} \\ $$$${it}\:{comes}\:{in}\:{contact}\:{with}\:{xz},\:{and} \\ $$$${yz}\:{plane}\:{simultaneously}\:? \\ $$
Answered by MrW3 last updated on 29/Oct/18
Commented by MrW3 last updated on 30/Oct/18
![ΔABC represents the plane which the circle lies in. The circle is the inscribed circle of the triangle ΔABC. A(a,0,0) B(0,b,0) C(0,0,c) we need to determine a,b and c. G(h,k,0) let ∠OAB=α ⇒AG=(k/(sin α)), GB=(h/(cos α)) AB=AG+GB ⇒AB=(k/(sin α))+(h/(cos α)) tan (A/2)=(R/(AG))=((R sin α)/k) tan (B/2)=(R/(GB))=((R cos α)/h) AC=AP+PC=AG+(R/(tan (C/2)))=(k/(sin α))+(R/(tan ((π−A−B)/2))) AC=(k/(sin α))+R tan ((A/2)+(B/2))=(k/(sin α))+R((((R sin α)/k)+((R cos α)/h))/(1−((R^2 sin α cos α)/(hk)))) ⇒AC=(k/(sin α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α)) BC=BQ+QC=GB+PC ⇒BC=(h/(cos α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α)) AB^2 =a^2 +b^2 AC^2 =a^2 +c^2 BC^2 =b^2 +c^2 ⇒a^2 +b^2 +c^2 =((AB^2 +AC^2 +BC^2 )/2) ⇒a^2 =((AB^2 +AC^2 −BC^2 )/2)=(([(k/(sin α))+(h/(cos α))]^2 +[(k/(sin α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 −[(h/(cos α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 )/2) ...(i) ⇒b^2 =((AB^2 −AC^2 +BC^2 )/2)=(([(k/(sin α))+(h/(cos α))]^2 −[(k/(sin α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 +[(h/(cos α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 )/2) ...(ii) ⇒c^2 =((−AB^2 +AC^2 +BC^2 )/2)=((−[(k/(sin α))+(h/(cos α))]^2 +[(k/(sin α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 +[(h/(cos α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 )/2) ...(iii) on the other side we have AC^2 −(AB cos α)^2 =BC^2 −(AB sin α)^2 AC^2 −BC^2 =AB^2 (cos^2 α−sin^2 α)=cos 2α AB^2 ⇒[(k/(sin α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 −[(h/(cos α))+((R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))]^2 =cos 2α [(k/(sin α))+(h/(cos α))]^2 ⇒[(k/(sin α))+(h/(cos α))+((2R^2 (h sin α+k cos α))/(hk−R^2 sin α cos α))][(k/(sin α))−(h/(cos α))]=cos 2α [(k/(sin α))+(h/(cos α))]^2 ⇒(((2hk)/R^2 )+sin 2α)((k/h)−tan α)=(((2hk)/R^2 )−sin 2α)((k/h)+tan α)cos 2α ...(iv) let t=tan α, μ=(k/h), λ=(R^2 /(hk)) ⇒(μ−λ)t^3 −t^2 +μt+(μλ−1)=0 ...(v) from (v) we get α, with this α we can get a,b and c from (i) to (iii). let d=altitude from O to AB (1/2)d×AB=(1/2)ab⇒d=((ab)/(AB))=((ab)/((k/(sin α))+(h/(cos α))))=((ab sin α cos α)/(k cos α+h sin α)) tan θ=(d/c) ⇒θ=tan^(−1) ((ab sin α cos α)/(c(k cos α+h sin α)))](Q46635.png)
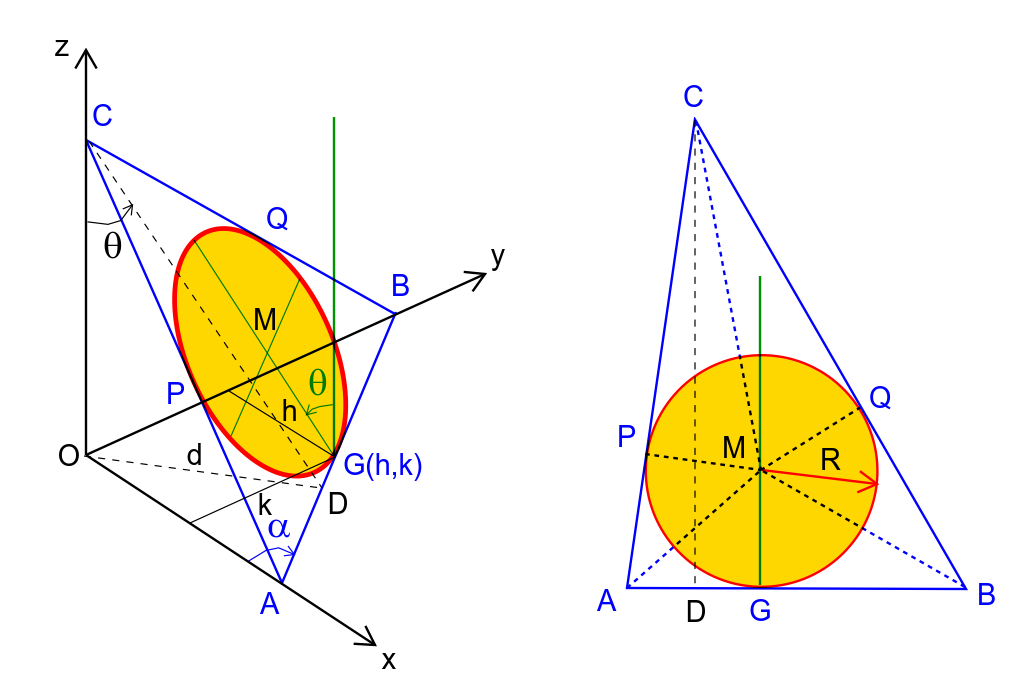
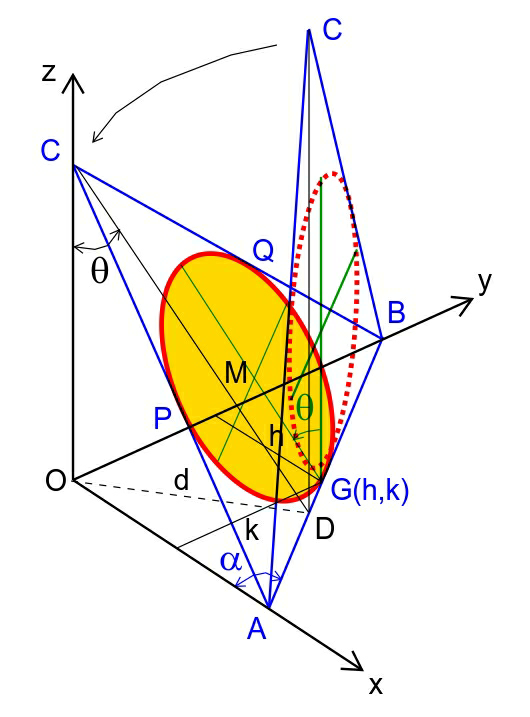
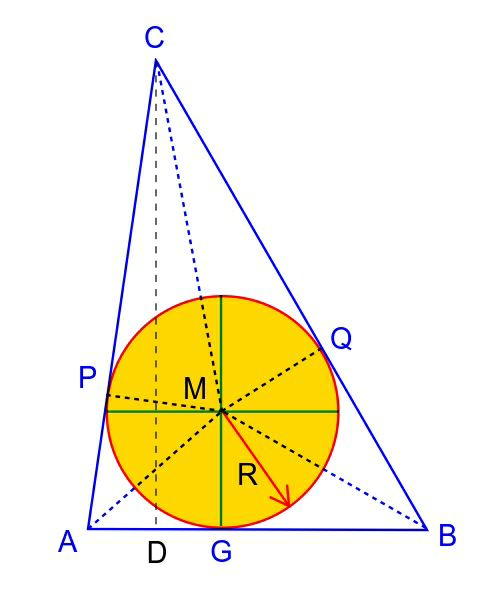
$$\Delta{ABC}\:{represents}\:{the}\:{plane}\:{which}\:{the} \\ $$$${circle}\:{lies}\:{in}.\:{The}\:{circle}\:{is}\:{the}\:{inscribed} \\ $$$${circle}\:{of}\:{the}\:{triangle}\:\Delta{ABC}. \\ $$$${A}\left({a},\mathrm{0},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{0},{b},\mathrm{0}\right) \\ $$$${C}\left(\mathrm{0},\mathrm{0},{c}\right) \\ $$$${we}\:{need}\:{to}\:{determine}\:{a},{b}\:{and}\:{c}. \\ $$$$ \\ $$$${G}\left({h},{k},\mathrm{0}\right) \\ $$$${let}\:\angle{OAB}=\alpha \\ $$$$\Rightarrow{AG}=\frac{{k}}{\mathrm{sin}\:\alpha},\:{GB}=\frac{{h}}{\mathrm{cos}\:\alpha} \\ $$$${AB}={AG}+{GB} \\ $$$$\Rightarrow{AB}=\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha} \\ $$$$\mathrm{tan}\:\frac{{A}}{\mathrm{2}}=\frac{{R}}{{AG}}=\frac{{R}\:\mathrm{sin}\:\alpha}{{k}} \\ $$$$\mathrm{tan}\:\frac{{B}}{\mathrm{2}}=\frac{{R}}{{GB}}=\frac{{R}\:\mathrm{cos}\:\alpha}{{h}} \\ $$$${AC}={AP}+{PC}={AG}+\frac{{R}}{\mathrm{tan}\:\frac{{C}}{\mathrm{2}}}=\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{R}}{\mathrm{tan}\:\frac{\pi−{A}−{B}}{\mathrm{2}}} \\ $$$${AC}=\frac{{k}}{\mathrm{sin}\:\alpha}+{R}\:\mathrm{tan}\:\left(\frac{{A}}{\mathrm{2}}+\frac{{B}}{\mathrm{2}}\right)=\frac{{k}}{\mathrm{sin}\:\alpha}+{R}\frac{\frac{{R}\:\mathrm{sin}\:\alpha}{{k}}+\frac{{R}\:\mathrm{cos}\:\alpha}{{h}}}{\mathrm{1}−\frac{{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}{{hk}}} \\ $$$$\Rightarrow{AC}=\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha} \\ $$$${BC}={BQ}+{QC}={GB}+{PC} \\ $$$$\Rightarrow{BC}=\frac{{h}}{\mathrm{cos}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha} \\ $$$$ \\ $$$${AB}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${AC}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$${BC}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\frac{{AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{{AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} −{BC}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} +\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} −\left[\frac{{h}}{\mathrm{cos}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} }{\mathrm{2}}\:\:...\left({i}\right) \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\frac{{AB}^{\mathrm{2}} −{AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} −\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} +\left[\frac{{h}}{\mathrm{cos}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} }{\mathrm{2}}\:\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\frac{−{AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} }{\mathrm{2}}=\frac{−\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} +\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} +\left[\frac{{h}}{\mathrm{cos}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} }{\mathrm{2}}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$${on}\:{the}\:{other}\:{side}\:{we}\:{have} \\ $$$${AC}^{\mathrm{2}} −\left({AB}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} ={BC}^{\mathrm{2}} −\left({AB}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} \\ $$$${AC}^{\mathrm{2}} −{BC}^{\mathrm{2}} ={AB}^{\mathrm{2}} \:\left(\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{sin}^{\mathrm{2}} \:\alpha\right)=\mathrm{cos}\:\mathrm{2}\alpha\:{AB}^{\mathrm{2}} \\ $$$$\Rightarrow\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} −\left[\frac{{h}}{\mathrm{cos}\:\alpha}+\frac{{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} =\mathrm{cos}\:\mathrm{2}\alpha\:\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}+\frac{\mathrm{2}{R}^{\mathrm{2}} \left({h}\:\mathrm{sin}\:\alpha+{k}\:\mathrm{cos}\:\alpha\right)}{{hk}−{R}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}\right]\left[\frac{{k}}{\mathrm{sin}\:\alpha}−\frac{{h}}{\mathrm{cos}\:\alpha}\right]=\mathrm{cos}\:\mathrm{2}\alpha\:\left[\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{\mathrm{2}{hk}}{{R}^{\mathrm{2}} }+\mathrm{sin}\:\mathrm{2}\alpha\right)\left(\frac{{k}}{{h}}−\mathrm{tan}\:\alpha\right)=\left(\frac{\mathrm{2}{hk}}{{R}^{\mathrm{2}} }−\mathrm{sin}\:\mathrm{2}\alpha\right)\left(\frac{{k}}{{h}}+\mathrm{tan}\:\alpha\right)\mathrm{cos}\:\mathrm{2}\alpha\:\:\:...\left({iv}\right) \\ $$$${let}\:{t}=\mathrm{tan}\:\alpha,\:\mu=\frac{{k}}{{h}},\:\lambda=\frac{{R}^{\mathrm{2}} }{{hk}} \\ $$$$\Rightarrow\left(\mu−\lambda\right){t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mu{t}+\left(\mu\lambda−\mathrm{1}\right)=\mathrm{0}\:\:\:...\left({v}\right) \\ $$$$ \\ $$$${from}\:\left({v}\right)\:{we}\:{get}\:\alpha,\:{with}\:{this}\:\alpha\:{we}\:{can} \\ $$$${get}\:{a},{b}\:{and}\:{c}\:{from}\:\left({i}\right)\:{to}\:\left({iii}\right). \\ $$$$ \\ $$$${let}\:{d}={altitude}\:{from}\:{O}\:{to}\:{AB} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{d}×{AB}=\frac{\mathrm{1}}{\mathrm{2}}{ab}\Rightarrow{d}=\frac{{ab}}{{AB}}=\frac{{ab}}{\frac{{k}}{\mathrm{sin}\:\alpha}+\frac{{h}}{\mathrm{cos}\:\alpha}}=\frac{{ab}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}{{k}\:\mathrm{cos}\:\alpha+{h}\:\mathrm{sin}\:\alpha} \\ $$$$\mathrm{tan}\:\theta=\frac{{d}}{{c}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{{ab}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}{{c}\left({k}\:\mathrm{cos}\:\alpha+{h}\:\mathrm{sin}\:\alpha\right)} \\ $$
Commented by MrW3 last updated on 30/Oct/18
Commented by ajfour last updated on 30/Oct/18
$$\mathcal{GREAT}\:\:{solution}\:{Sir}, \\ $$$$\mathcal{T}{hanks}\:! \\ $$
Commented by MrW3 last updated on 30/Oct/18
Commented by MrW3 last updated on 30/Oct/18
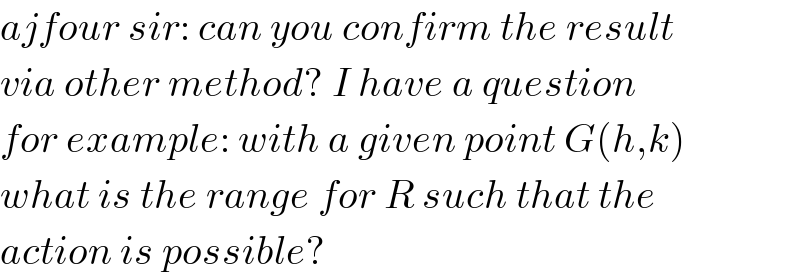
$${ajfour}\:{sir}:\:{can}\:{you}\:{confirm}\:{the}\:{result} \\ $$$${via}\:{other}\:{method}?\:{I}\:{have}\:{a}\:{question} \\ $$$${for}\:{example}:\:{with}\:{a}\:{given}\:{point}\:{G}\left({h},{k}\right) \\ $$$${what}\:{is}\:{the}\:{range}\:{for}\:{R}\:{such}\:{that}\:{the} \\ $$$${action}\:{is}\:{possible}? \\ $$
Commented by MrW3 last updated on 30/Oct/18
Commented by MrW3 last updated on 30/Oct/18
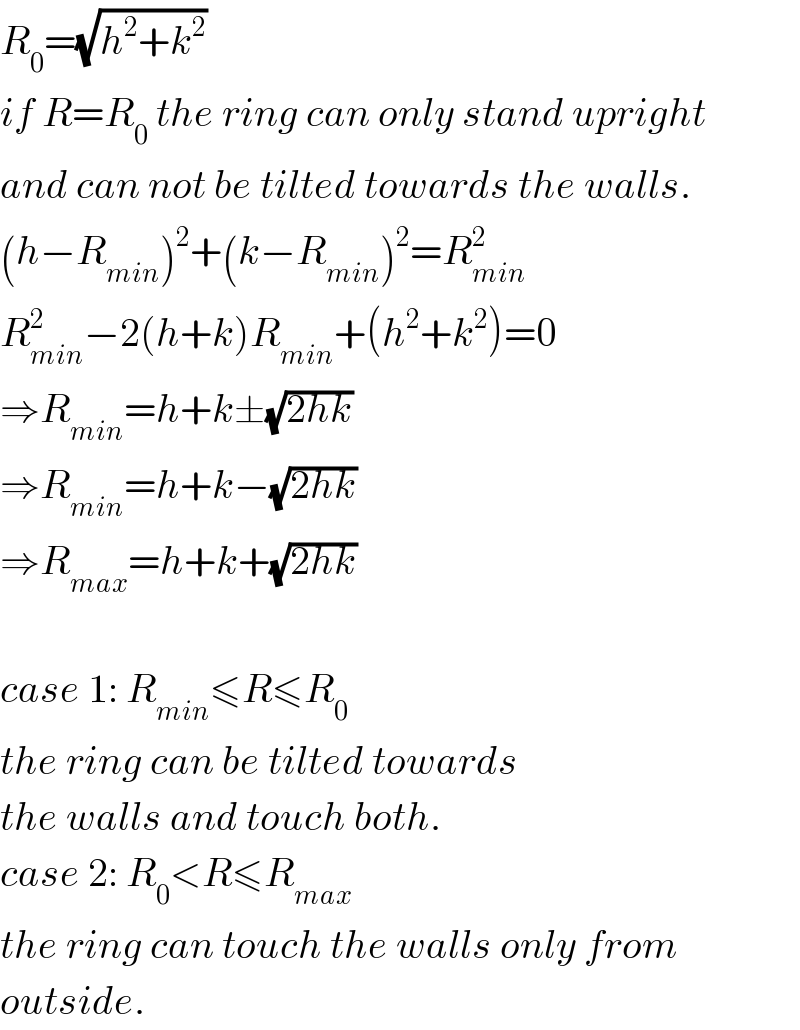
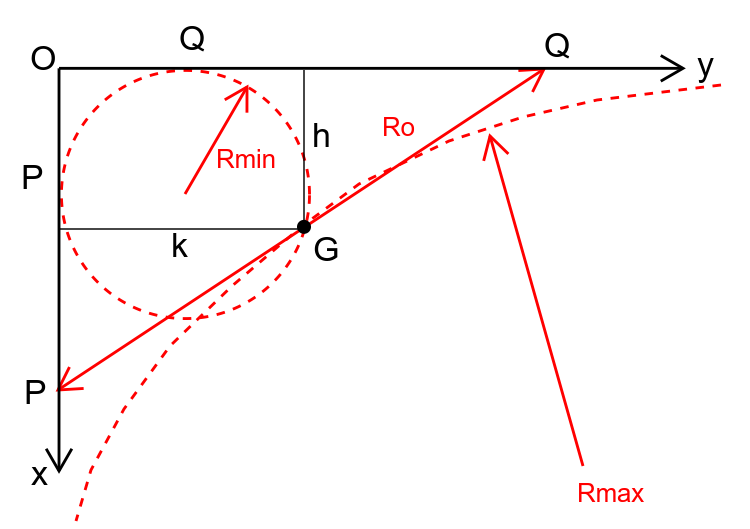
$${R}_{\mathrm{0}} =\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} } \\ $$$${if}\:{R}={R}_{\mathrm{0}} \:{the}\:{ring}\:{can}\:{only}\:{stand}\:{upright} \\ $$$${and}\:{can}\:{not}\:{be}\:{tilted}\:{towards}\:{the}\:{walls}. \\ $$$$\left({h}−{R}_{{min}} \right)^{\mathrm{2}} +\left({k}−{R}_{{min}} \right)^{\mathrm{2}} ={R}_{{min}} ^{\mathrm{2}} \\ $$$${R}_{{min}} ^{\mathrm{2}} −\mathrm{2}\left({h}+{k}\right){R}_{{min}} +\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{R}_{{min}} ={h}+{k}\pm\sqrt{\mathrm{2}{hk}} \\ $$$$\Rightarrow{R}_{{min}} ={h}+{k}−\sqrt{\mathrm{2}{hk}} \\ $$$$\Rightarrow{R}_{{max}} ={h}+{k}+\sqrt{\mathrm{2}{hk}} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:{R}_{{min}} \leqslant{R}\leqslant{R}_{\mathrm{0}} \\ $$$${the}\:{ring}\:{can}\:{be}\:{tilted}\:{towards} \\ $$$${the}\:{walls}\:{and}\:{touch}\:{both}. \\ $$$${case}\:\mathrm{2}:\:{R}_{\mathrm{0}} <{R}\leqslant{R}_{{max}} \\ $$$${the}\:{ring}\:{can}\:{touch}\:{the}\:{walls}\:{only}\:{from} \\ $$$${outside}. \\ $$
Commented by ajfour last updated on 31/Oct/18

$${I}\:{couldn}'{t}\:{find}\:{any}\:{good}\:{way}\:,\:{Sir} \\ $$$${and}\:{was}\:{busy}\:{unentangling}\:{my} \\ $$$${hands}! \\ $$
Commented by MrW3 last updated on 31/Oct/18
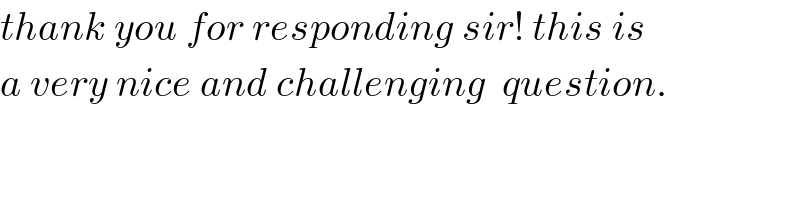
$${thank}\:{you}\:{for}\:{responding}\:{sir}!\:{this}\:{is} \\ $$$${a}\:{very}\:{nice}\:{and}\:{challenging}\:\:{question}. \\ $$
Commented by ajfour last updated on 31/Oct/18
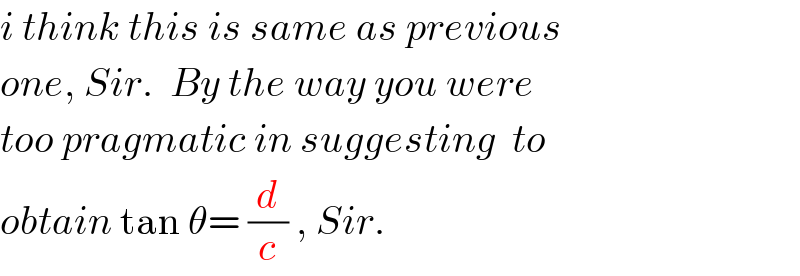
$${i}\:{think}\:{this}\:{is}\:{same}\:{as}\:{previous}\: \\ $$$${one},\:{Sir}.\:\:{By}\:{the}\:{way}\:{you}\:{were} \\ $$$${too}\:{pragmatic}\:{in}\:{suggesting}\:\:{to} \\ $$$${obtain}\:\mathrm{tan}\:\theta=\:\frac{{d}}{{c}}\:,\:{Sir}. \\ $$
Answered by MrW3 last updated on 01/Nov/18
Commented by MrW3 last updated on 01/Nov/18
![another (better) way to solve: the projection of the circle in the xy−plane is an ellipse which has the semi−major axis R and tangents x−axis and y−axis simultaneously. assume the semi−minor axis of ellipse is d. in coordinate system x′y′ the eqn. of ellipse is (x^2 /R^2 )+(y^2 /d^2 )=1 GA=(k/(sin α)), GB=(h/(cos α)) eqn. of line OA in x′y′ system is ((y−d)/(x−(k/(sin α))))=tan α ⇒sin α x−cos α y+d cos α−k=0 since it′s a tangent line of ellipse, R^2 sin^2 α+d^2 cos^2 α−(d cos α−k)^2 =0 ⇒R^2 sin^2 α−k^2 +2dk cos α=0 ...(i) eqn. of line OB in x′y′ system is ((y−d)/(x+(h/(cos α))))=−(1/(tan α)) ⇒cos α x+sin α y+h−d sin α=0 since it′s a tangent line of ellipse, R^2 cos^2 α+q^2 sin^2 α−(h−d sin α)^2 =0 ⇒R^2 cos^2 α−h^2 +2dh sin α=0 ...(ii) (i)+(ii): R^2 −k^2 −h^2 +2d(k cos α+h sin α)=0 ⇒d=((k^2 +h^2 −R^2 )/(2(k cos α+h sin α))) ...(iii) put this into (ii): R^2 cos^2 α+((h(k^2 +h^2 −R^2 )sin α)/(k cos α+h sin α))=h^2 ⇒((R/h))^2 (1/(1+tan^2 α))+((1+((k/h))^2 −((R/h))^2 )/(1+((k/h))(1/(tan α))))=1 ...(iv) or with t=tan α, λ=(R/h), μ=(k/h) ⇒(μ^2 −λ^2 )t^3 −μt^2 +μ^2 t+μ(λ^2 −1)=0 ...(iv) from (iv) we can get α at first. then we get d from (iii). sin θ=(d/R)=((k^2 +h^2 −R^2 )/(2R(k cos α+h sin α))) ⇒θ=sin^(−1) ((1+((k/h))^2 −((R/h))^2 )/(2((R/h))[sin α+((k/h))cos α])) examples: h=4, k=3, R=4: ⇒α=0°, 29.4346° ⇒θ=22.024°, 14.225° h=3, k=3, R=2.5: ⇒α=30.8212°, 45°, 59.1788° ⇒θ=34.842°, 33.635°, 34.842°](Q46822.png)
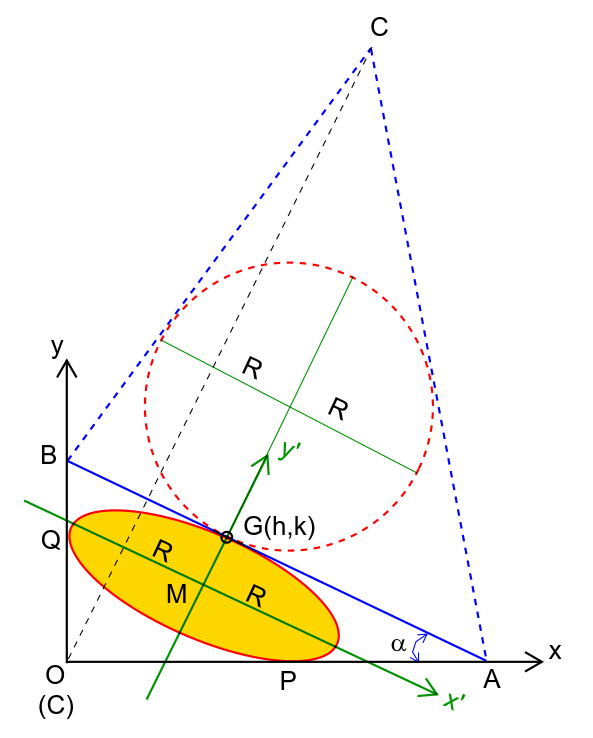
$${another}\:\left({better}\right)\:{way}\:{to}\:{solve}: \\ $$$$ \\ $$$${the}\:{projection}\:{of}\:{the}\:{circle}\:{in}\:{the} \\ $$$${xy}−{plane}\:{is}\:{an}\:{ellipse}\:{which}\:{has}\:{the} \\ $$$${semi}−{major}\:{axis}\:{R}\:{and}\:{tangents} \\ $$$${x}−{axis}\:{and}\:{y}−{axis}\:{simultaneously}. \\ $$$$ \\ $$$${assume}\:{the}\:{semi}−{minor}\:{axis}\:{of}\:{ellipse} \\ $$$${is}\:{d}. \\ $$$${in}\:{coordinate}\:{system}\:{x}'{y}'\:{the}\:{eqn}. \\ $$$${of}\:{ellipse}\:{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{{R}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{d}^{\mathrm{2}} }=\mathrm{1} \\ $$$${GA}=\frac{{k}}{\mathrm{sin}\:\alpha},\:{GB}=\frac{{h}}{\mathrm{cos}\:\alpha} \\ $$$$ \\ $$$${eqn}.\:{of}\:{line}\:{OA}\:{in}\:{x}'{y}'\:{system}\:{is} \\ $$$$\frac{{y}−{d}}{{x}−\frac{{k}}{\mathrm{sin}\:\alpha}}=\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\mathrm{sin}\:\alpha\:{x}−\mathrm{cos}\:\alpha\:{y}+{d}\:\mathrm{cos}\:\alpha−{k}=\mathrm{0} \\ $$$${since}\:{it}'{s}\:{a}\:{tangent}\:{line}\:{of}\:{ellipse}, \\ $$$${R}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\alpha+{d}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha−\left({d}\:\mathrm{cos}\:\alpha−{k}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{R}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\alpha−{k}^{\mathrm{2}} +\mathrm{2}{dk}\:\mathrm{cos}\:\alpha=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$ \\ $$$${eqn}.\:{of}\:{line}\:{OB}\:{in}\:{x}'{y}'\:{system}\:{is} \\ $$$$\frac{{y}−{d}}{{x}+\frac{{h}}{\mathrm{cos}\:\alpha}}=−\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha\:{x}+\mathrm{sin}\:\alpha\:{y}+{h}−{d}\:\mathrm{sin}\:\alpha=\mathrm{0} \\ $$$${since}\:{it}'{s}\:{a}\:{tangent}\:{line}\:{of}\:{ellipse}, \\ $$$${R}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\alpha−\left({h}−{d}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{R}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha−{h}^{\mathrm{2}} +\mathrm{2}{dh}\:\mathrm{sin}\:\alpha=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${R}^{\mathrm{2}} −{k}^{\mathrm{2}} −{h}^{\mathrm{2}} +\mathrm{2}{d}\left({k}\:\mathrm{cos}\:\alpha+{h}\:\mathrm{sin}\:\alpha\right)=\mathrm{0} \\ $$$$\Rightarrow{d}=\frac{{k}^{\mathrm{2}} +{h}^{\mathrm{2}} −{R}^{\mathrm{2}} }{\mathrm{2}\left({k}\:\mathrm{cos}\:\alpha+{h}\:\mathrm{sin}\:\alpha\right)}\:\:\:...\left({iii}\right) \\ $$$${put}\:{this}\:{into}\:\left({ii}\right): \\ $$$${R}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha+\frac{{h}\left({k}^{\mathrm{2}} +{h}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)\mathrm{sin}\:\alpha}{{k}\:\mathrm{cos}\:\alpha+{h}\:\mathrm{sin}\:\alpha}={h}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{{R}}{{h}}\right)^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}+\frac{\mathrm{1}+\left(\frac{{k}}{{h}}\right)^{\mathrm{2}} −\left(\frac{{R}}{{h}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{k}}{{h}}\right)\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}}=\mathrm{1}\:\:...\left({iv}\right) \\ $$$${or}\:{with}\:{t}=\mathrm{tan}\:\alpha,\:\lambda=\frac{{R}}{{h}},\:\mu=\frac{{k}}{{h}} \\ $$$$\Rightarrow\left(\mu^{\mathrm{2}} −\lambda^{\mathrm{2}} \right){t}^{\mathrm{3}} −\mu{t}^{\mathrm{2}} +\mu^{\mathrm{2}} {t}+\mu\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0}\:\:\:...\left({iv}\right) \\ $$$$ \\ $$$${from}\:\left({iv}\right)\:{we}\:{can}\:{get}\:\alpha\:{at}\:{first}. \\ $$$${then}\:{we}\:{get}\:{d}\:{from}\:\left({iii}\right). \\ $$$$ \\ $$$$\mathrm{sin}\:\theta=\frac{{d}}{{R}}=\frac{{k}^{\mathrm{2}} +{h}^{\mathrm{2}} −{R}^{\mathrm{2}} }{\mathrm{2}{R}\left({k}\:\mathrm{cos}\:\alpha+{h}\:\mathrm{sin}\:\alpha\right)} \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}+\left(\frac{{k}}{{h}}\right)^{\mathrm{2}} −\left(\frac{{R}}{{h}}\right)^{\mathrm{2}} }{\mathrm{2}\left(\frac{{R}}{{h}}\right)\left[\mathrm{sin}\:\alpha+\left(\frac{{k}}{{h}}\right)\mathrm{cos}\:\:\alpha\right]} \\ $$$$ \\ $$$${examples}: \\ $$$${h}=\mathrm{4},\:{k}=\mathrm{3},\:{R}=\mathrm{4}: \\ $$$$\Rightarrow\alpha=\mathrm{0}°,\:\mathrm{29}.\mathrm{4346}° \\ $$$$\Rightarrow\theta=\mathrm{22}.\mathrm{024}°,\:\mathrm{14}.\mathrm{225}° \\ $$$$ \\ $$$${h}=\mathrm{3},\:{k}=\mathrm{3},\:{R}=\mathrm{2}.\mathrm{5}: \\ $$$$\Rightarrow\alpha=\mathrm{30}.\mathrm{8212}°,\:\mathrm{45}°,\:\mathrm{59}.\mathrm{1788}° \\ $$$$\Rightarrow\theta=\mathrm{34}.\mathrm{842}°,\:\mathrm{33}.\mathrm{635}°,\:\mathrm{34}.\mathrm{842}° \\ $$
Commented by ajfour last updated on 01/Nov/18
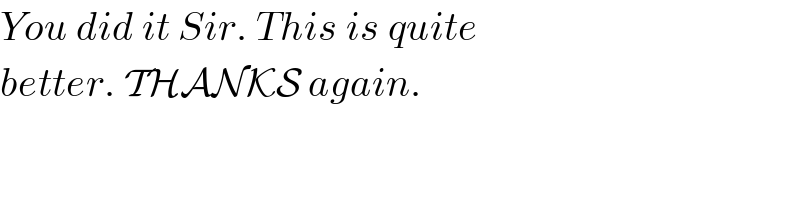
$${You}\:{did}\:{it}\:{Sir}.\:{This}\:{is}\:{quite} \\ $$$${better}.\:\mathcal{THANKS}\:{again}. \\ $$
Commented by ajfour last updated on 02/Nov/18
$${I}\:{have}\:{posted}\:{an}\:{alternate}\:{way},\:{Sir}. \\ $$
