Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 46612 by maxmathsup by imad last updated on 29/Oct/18

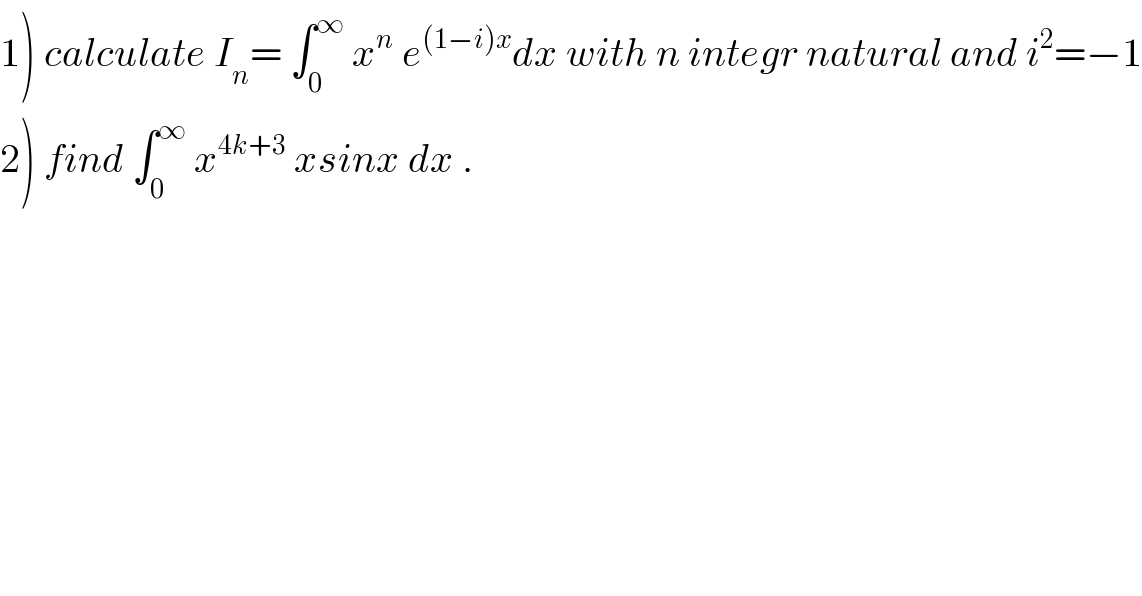
1) calculate I_n = ∫_0 ^∞ x^n e^((1−i)x) dx with n integr natural and i^2 =−1 2) find ∫_0 ^∞ x^(4k+3) xsinx dx .

$$\left.\mathrm{1}\right)\:{calculate}\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:{x}^{{n}} \:{e}^{\left(\mathrm{1}−{i}\right){x}} {dx}\:{with}\:{n}\:{integr}\:{natural}\:{and}\:{i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:{find}\:\int_{\mathrm{0}} ^{\infty} \:{x}^{\mathrm{4}{k}+\mathrm{3}} \:{xsinx}\:{dx}\:. \\ $$

Commented by maxmathsup by imad last updated on 29/Oct/18

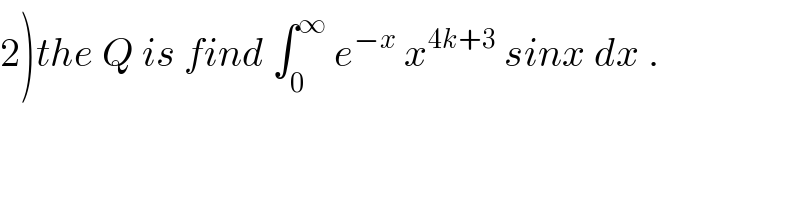
2)the Q is find ∫_0 ^∞ e^(−x) x^(4k+3) sinx dx .

$$\left.\mathrm{2}\right){the}\:{Q}\:{is}\:{find}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} \:{x}^{\mathrm{4}{k}+\mathrm{3}} \:{sinx}\:{dx}\:. \\ $$

Commented by maxmathsup by imad last updated on 29/Oct/18

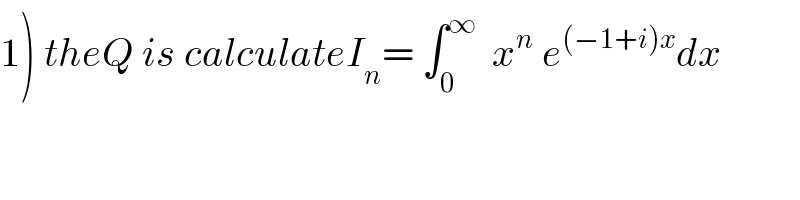
1) theQ is calculateI_n = ∫_0 ^∞ x^n e^((−1+i)x) dx

$$\left.\mathrm{1}\right)\:{theQ}\:{is}\:{calculateI}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:{x}^{{n}} \:{e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}\: \\ $$

Commented by maxmathsup by imad last updated on 29/Oct/18

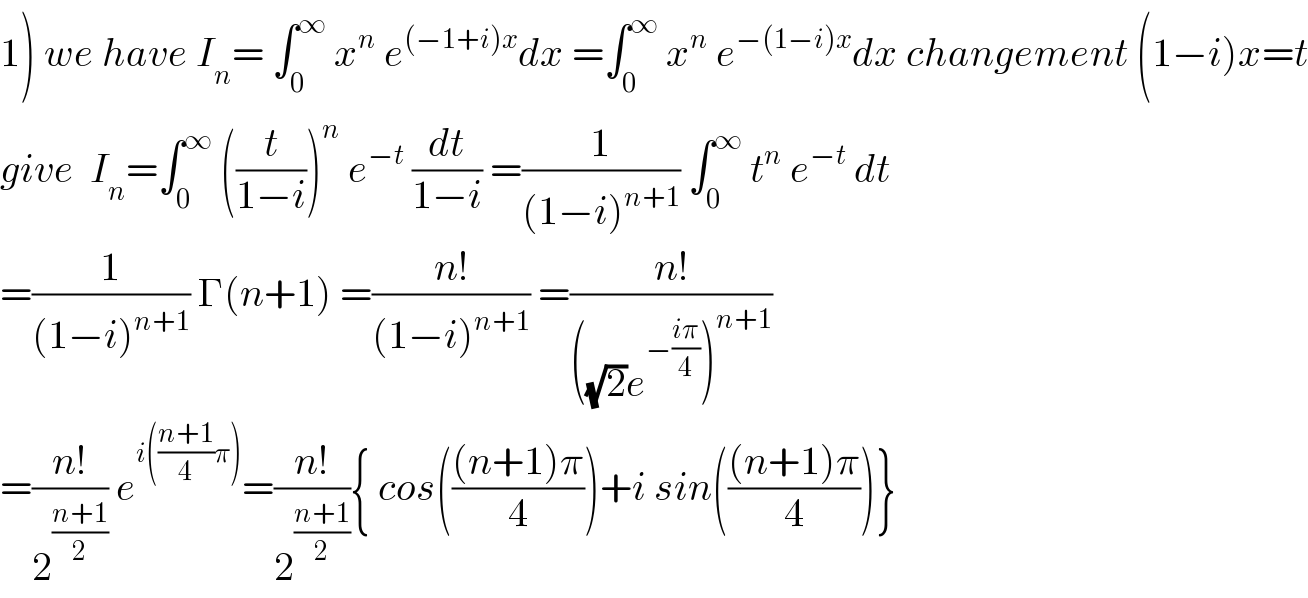
1) we have I_n = ∫_0 ^∞ x^n e^((−1+i)x) dx =∫_0 ^∞ x^n e^(−(1−i)x) dx changement (1−i)x=t give I_n =∫_0 ^∞ ((t/(1−i)))^n e^(−t) (dt/(1−i)) =(1/((1−i)^(n+1) )) ∫_0 ^∞ t^n e^(−t) dt =(1/((1−i)^(n+1) )) Γ(n+1) =((n!)/((1−i)^(n+1) )) =((n!)/(((√2)e^(−((iπ)/4)) )^(n+1) )) =((n!)/2^((n+1)/2) ) e^(i(((n+1)/4)π)) =((n!)/2^((n+1)/2) ){ cos((((n+1)π)/4))+i sin((((n+1)π)/4))}

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:{x}^{{n}} \:{e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}\:=\int_{\mathrm{0}} ^{\infty} \:{x}^{{n}} \:{e}^{−\left(\mathrm{1}−{i}\right){x}} {dx}\:{changement}\:\left(\mathrm{1}−{i}\right){x}={t} \\ $$$${give}\:\:{I}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\left(\frac{{t}}{\mathrm{1}−{i}}\right)^{{n}} \:{e}^{−{t}} \:\frac{{dt}}{\mathrm{1}−{i}}\:=\frac{\mathrm{1}}{\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} }\:\Gamma\left({n}+\mathrm{1}\right)\:=\frac{{n}!}{\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} }\:=\frac{{n}!}{\left(\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} } \\ $$$$=\frac{{n}!}{\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} }\:{e}^{{i}\left(\frac{{n}+\mathrm{1}}{\mathrm{4}}\pi\right)} =\frac{{n}!}{\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} }\left\{\:{cos}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{4}}\right)+{i}\:{sin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{4}}\right)\right\} \\ $$

Commented by maxmathsup by imad last updated on 29/Oct/18

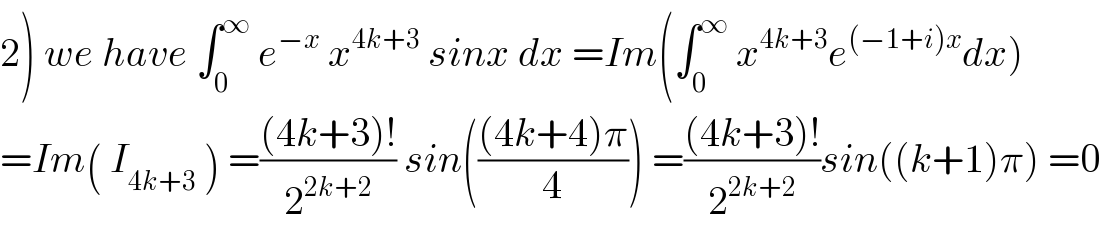
2) we have ∫_0 ^∞ e^(−x) x^(4k+3) sinx dx =Im(∫_0 ^∞ x^(4k+3) e^((−1+i)x) dx) =Im( I_(4k+3) ) =(((4k+3)!)/2^(2k+2) ) sin((((4k+4)π)/4)) =(((4k+3)!)/2^(2k+2) )sin((k+1)π) =0

$$\left.\mathrm{2}\right)\:{we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} \:{x}^{\mathrm{4}{k}+\mathrm{3}} \:{sinx}\:{dx}\:={Im}\left(\int_{\mathrm{0}} ^{\infty} \:{x}^{\mathrm{4}{k}+\mathrm{3}} {e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}\right) \\ $$$$={Im}\left(\:{I}_{\mathrm{4}{k}+\mathrm{3}} \:\right)\:=\frac{\left(\mathrm{4}{k}+\mathrm{3}\right)!}{\mathrm{2}^{\mathrm{2}{k}+\mathrm{2}} }\:{sin}\left(\frac{\left(\mathrm{4}{k}+\mathrm{4}\right)\pi}{\mathrm{4}}\right)\:=\frac{\left(\mathrm{4}{k}+\mathrm{3}\right)!}{\mathrm{2}^{\mathrm{2}{k}+\mathrm{2}} }{sin}\left(\left({k}+\mathrm{1}\right)\pi\right)\:=\mathrm{0} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 29/Oct/18

(1−i)x=−t [ t=(i−1)x] dx=((−dt)/((1−i))) ∫_0 ^∞ (t^n /((i−1)^n ))×e^(−t) ×((−dt)/((1−i))) (1/((i−1)^(n+1) ))∫_0 ^∞ e^(−t) t^(n+1−1) dt (1/((i−1)^(n+1) ))×⌈(n+1) (1/((i−1)^(n+1) ))×n! =(((−1)^(n+1) )/((1−i)^(n+1) ))×(((1+i)^(n+1) )/((1+i)^(n+1) ))×n! =(((−1)^(n+1) )/((2)^(n+1) ))×{(√2) ((1/((√2) ))+i×(1/(√2)))}^(n+1) ×n! =(((−1)^(n+1) )/2^((n+1)/2) )×{cos(π/4)+isin(π/4)}^(n+1) ×n! =(((−1)^(n+1) )/2^((n+1)/2) )×{cos(2kπ+(π/4))+isin(2kπ+(π/4))}^(n+1) ×n!

$$\left(\mathrm{1}−{i}\right){x}=−{t}\:\:\:\:\:\:\:\:\:\:\:\left[\:\:{t}=\left({i}−\mathrm{1}\right){x}\right] \\ $$$${dx}=\frac{−{dt}}{\left(\mathrm{1}−{i}\right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{n}} }{\left({i}−\mathrm{1}\right)^{{n}} }×{e}^{−{t}} \:×\frac{−{dt}}{\left(\mathrm{1}−{i}\right)} \\ $$$$\frac{\mathrm{1}}{\left({i}−\mathrm{1}\right)^{{n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{{n}+\mathrm{1}−\mathrm{1}} {dt} \\ $$$$\frac{\mathrm{1}}{\left({i}−\mathrm{1}\right)^{{n}+\mathrm{1}} }×\lceil\left({n}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\left({i}−\mathrm{1}\right)^{{n}+\mathrm{1}} }×{n}! \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} }×\frac{\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} }×{n}! \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{2}\right)^{{n}+\mathrm{1}} }×\left\{\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}+{i}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)\right\}^{{n}+\mathrm{1}} ×{n}! \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} }×\left\{{cos}\frac{\pi}{\mathrm{4}}+{isin}\frac{\pi}{\mathrm{4}}\right\}^{{n}+\mathrm{1}} ×{n}! \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} }×\left\{{cos}\left(\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}}\right)+{isin}\left(\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}}\right)\right\}^{{n}+\mathrm{1}} ×{n}! \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com