Question Number 4862 by prakash jain last updated on 18/Mar/16
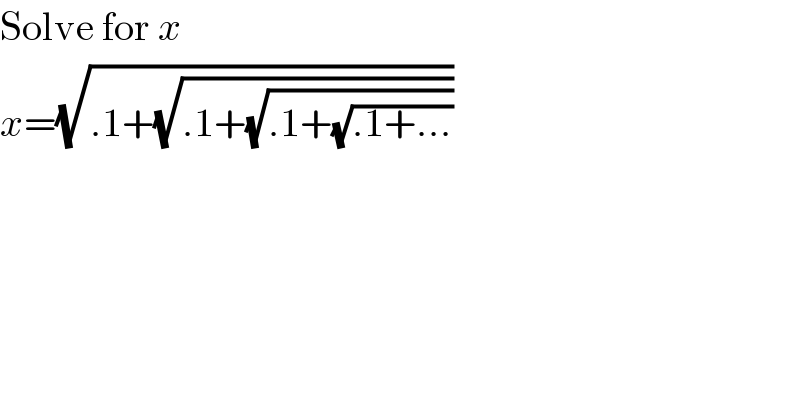
$$\mathrm{Solve}\:\mathrm{for}\:{x} \\ $$$${x}=\sqrt{.\mathrm{1}+\sqrt{.\mathrm{1}+\sqrt{.\mathrm{1}+\sqrt{.\mathrm{1}+...}}}} \\ $$
Answered by Yozzii last updated on 18/Mar/16

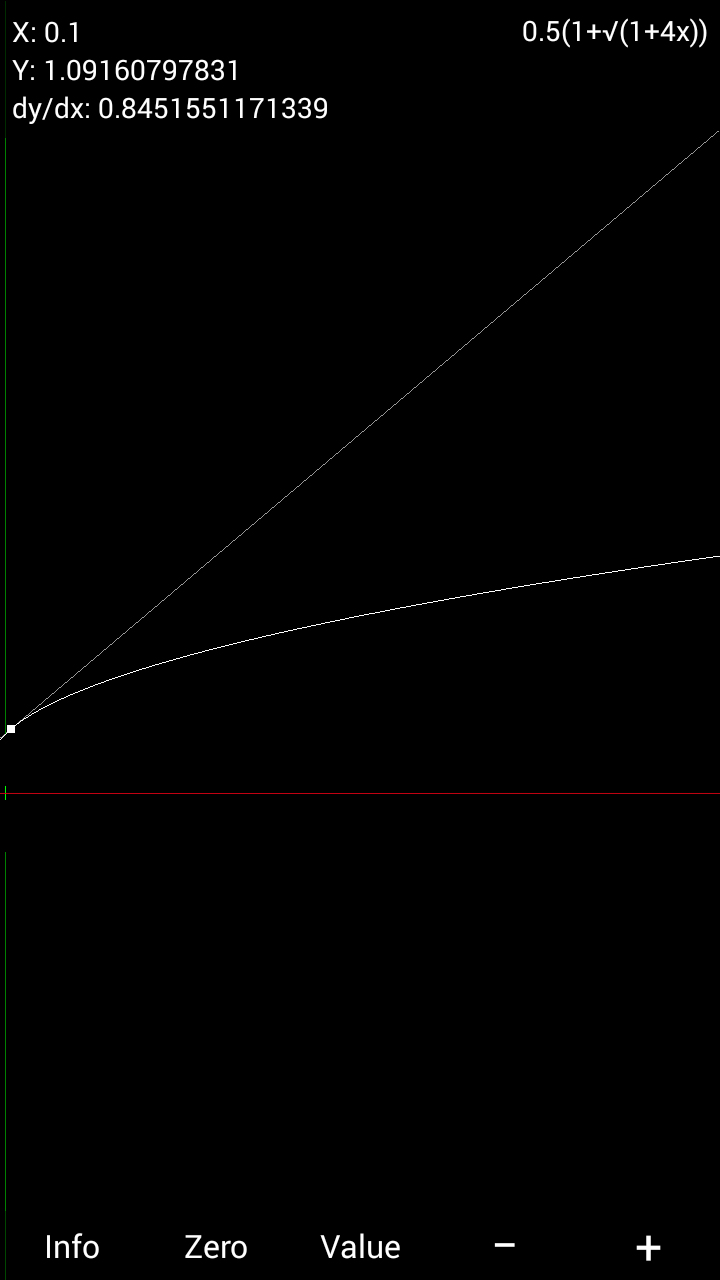
$${Let}\:{us}\:{look}\:{at}\:{the}\:{general}\:{case}\:{of} \\ $$$$\:\:\:\:\:{x}=\sqrt{{a}+\sqrt{{a}+\sqrt{{a}+\sqrt{{a}+\sqrt{{a}+...}}}}} \\ $$$${where}\:{a}\in\mathbb{C}.\:{Assuming}\:{then}\:{that}\:{the} \\ $$$${convergence}\:{of}\:{the}\:{value}\:{of}\:{x}\:{exists} \\ $$$${we}\:{can}\:{perform}\:{the}\:{following}\:{algebraic} \\ $$$${manipulation}. \\ $$$${x}^{\mathrm{2}} ={a}+\sqrt{{a}+\sqrt{{a}+\sqrt{{a}+\sqrt{{a}+...}}}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} ={a}+{x} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}−{a}=\mathrm{0}\:\:\left(\ast\right) \\ $$$${If}\:{x}\in\mathbb{R}\Rightarrow{the}\:{discriminant}\:{D}\:{of}\:\left(\ast\right) \\ $$$${is}\:{non}−{negative}. \\ $$$$\therefore{D}\geqslant\mathrm{0}\Rightarrow\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−{a}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{4}{a}\geqslant\mathrm{0}\Rightarrow{a}\geqslant−\mathrm{0}.\mathrm{25}.\:{Otherwise},{x}\notin\mathbb{R}\:{if}\:{a}<−\mathrm{0}.\mathrm{25}. \\ $$$${Then}\:{a}\in\mathbb{R}\:\left({for}\:{if}\:{a}\notin\mathbb{R},\:{a}\geqslant−\mathrm{0}.\mathrm{25}\:{is}\:{senseless}\right. \\ $$$$\left.{in}\:{the}\:{law}\:{of}\:{trichotomy}.\right) \\ $$$${In}\:{the}\:{given}\:{question},\:{a}=\mathrm{0}.\mathrm{1}>−\mathrm{0}.\mathrm{25}. \\ $$$$\Rightarrow\:{x}\in\mathbb{R}\:{and}\:{x}\geqslant\mathrm{0}\:{by}\:{the}\:{taking}\:{of}\:{the} \\ $$$${positive}\:{square}−{root}\:{of}\:{some}\: \\ $$$${non}−{negative}\:{real}\:{number}. \\ $$$$\therefore\:{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}{a}}}{\mathrm{2}}\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{a}}}{\mathrm{2}}\:{or}\:{x}=\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{a}}}{\mathrm{2}}. \\ $$$${If}\:{a}>\mathrm{0}\:{and}\:{x}\geqslant\mathrm{0}\Rightarrow{x}\neq\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{a}}}{\mathrm{2}} \\ $$$${so}\:{that}\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{a}}}{\mathrm{2}}.\:{a}=\mathrm{0}.\mathrm{1}>\mathrm{0} \\ $$$$\therefore\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{1}.\mathrm{4}}}{\mathrm{2}}. \\ $$$${If}\:−\mathrm{0}.\mathrm{25}\leqslant{a}<\mathrm{0}\:{then}\:\mathrm{0}\leqslant\mathrm{1}+\mathrm{4}{a}<\mathrm{1} \\ $$$$\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{a}}>\mathrm{0}\:{and}\:\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{a}}>\mathrm{0} \\ $$$$\Rightarrow{x}\:{is}\:{arbitrarily}\:{one}\:{of}\:{the}\:{two} \\ $$$${solutions}\:{found}\:{which}\:{means}\:{then} \\ $$$${that}\:{x}\:{has}\:{no}\:{real}\:{value}.\:{So}\:{a}\:{necessary} \\ $$$${and}\:{sufficient}\:{condition}\:{for}\:{a}\:{definitive} \\ $$$${convergence}\:{of}\:{x}\in\mathbb{R}\:{is}\:{that}\:{a}\geqslant\mathrm{0}\:. \\ $$$$ \\ $$$${If}\:{x}\notin\mathbb{R}\Rightarrow\mathrm{1}+\mathrm{4}{a}<\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}\pm{i}\sqrt{−\mathrm{1}−\mathrm{4}{a}}}{\mathrm{2}}. \\ $$$${This}\:{similarly}\:{indicates}\:{that}\:{x}\:{is} \\ $$$${arbitrary}\:{at}\:\infty,\:{so}\:{that}\:{no}\:{such}\:{x}\notin\mathbb{R} \\ $$$${exists}\:{if}\:{a}<−\mathrm{0}.\mathrm{25}. \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 18/Mar/16
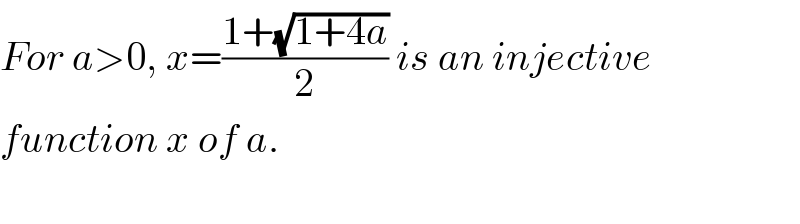
$${For}\:{a}>\mathrm{0},\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{a}}}{\mathrm{2}}\:{is}\:{an}\:{injective} \\ $$$${function}\:{x}\:{of}\:{a}.\: \\ $$$$ \\ $$
Commented by Yozzii last updated on 18/Mar/16