Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 49604 by Tawa1 last updated on 08/Dec/18

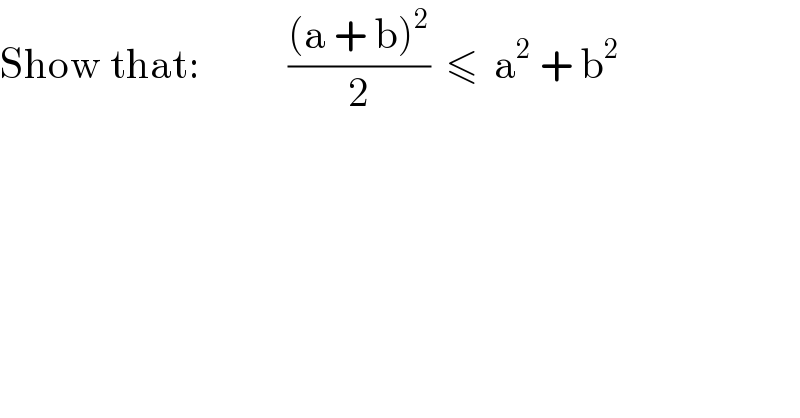
Show that: (((a + b)^2 )/2) ≤ a^2 + b^2

$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{a}\:+\:\mathrm{b}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\leqslant\:\:\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \\ $$

Answered by afachri last updated on 08/Dec/18

let (a − b)^2 ≥ 0 a^2 − 2ab + b^2 ≥ 0 a^2 + b^2 ≥ 2ab a^2 + 2ab + b^2 ≥ 2ab + 2ab (a + b)^2 ≥ 4(ab) meanwhile : ab = (( (a + b)^2 − (a^2 + b^2 ) )/2) (a + b)^2 ≥ 4((( (a + b)^2 − (a^2 + b^2 ))/2)) (a + b)^(2 ) ≥ 2(a + b)^2 − 2(a^2 + b^2 )] −(a + b)^2 ≥ −2(a^2 + b^2 ) (((a + b)^2 )/2) ≤ (a^2 + b^2 )

$$\mathrm{let}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:−\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} −\:\mathrm{2}{ab}\:+\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{2}{ab} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\:\mathrm{2}{ab}\:+\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{2}{ab}\:+\:\mathrm{2}{ab} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{4}\left({ab}\right) \\ $$$$ \\ $$$$\mathrm{meanwhile}\:\::\:\:{ab}\:\:=\:\:\frac{\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:−\:\:\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)\:}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:\:\mathrm{4}\left(\frac{\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:−\:\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)}{\mathrm{2}}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:+\:{b}\right)^{\mathrm{2}\:} \:\geqslant\:\:\mathrm{2}\left({a}\:+\:{b}\right)^{\mathrm{2}} \:−\:\mathrm{2}\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:−\left({a}\:+\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:−\mathrm{2}\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\left({a}\:+\:{b}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\leqslant\:\:\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right) \\ $$$$ \\ $$

Commented by Tawa1 last updated on 08/Dec/18

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$

Commented by Tawa1 last updated on 08/Dec/18

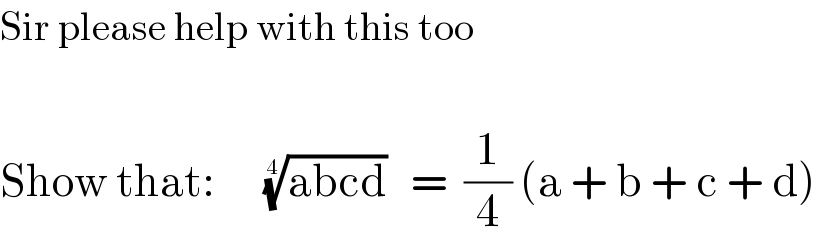
Sir please help with this too Show that: ((abcd))^(1/4) = (1/4) (a + b + c + d)

$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}\:\mathrm{too} \\ $$$$ \\ $$$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\:\:\sqrt[{\mathrm{4}}]{\mathrm{abcd}}\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\left(\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:+\:\mathrm{d}\right) \\ $$

Commented by afachri last updated on 08/Dec/18

Arithmaric Mean = ((a + b + c + d)/4) Geometric Mean = ((abcd^ ))^(1/4) Arithmatic Mean ≥ Geometric Mean (1/4)(a + b + c + d) ≥ ((abcd^ ))^(1/4) so, the equalty can be achieved only and if only : a = b= c = d then (1/4)(a + b + c + d) = ((abcd^ ))^(1/4)

$$\:\:\mathrm{Arithmaric}\:\mathrm{Mean}\:=\:\:\frac{{a}\:+\:{b}\:+\:{c}\:+\:{d}}{\mathrm{4}} \\ $$$$\:\:\mathrm{Geometric}\:\mathrm{Mean}\:\:=\:\:\sqrt[{\mathrm{4}}]{{abcd}^{} } \\ $$$$ \\ $$$$\:\:\mathrm{Arithmatic}\:\mathrm{Mean}\:\:\geqslant\:\:\mathrm{Geometric}\:\mathrm{Mean} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\left({a}\:+\:{b}\:+\:{c}\:+\:{d}\right)\:\:\geqslant\:\:\sqrt[{\mathrm{4}}]{{abcd}^{} }\: \\ $$$$\:\:\mathrm{so},\:\mathrm{the}\:\mathrm{equalty}\:\mathrm{can}\:\mathrm{be}\:\mathrm{achieved}\:\mathrm{only} \\ $$$$\:\:\mathrm{and}\:\mathrm{if}\:\mathrm{only}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\:=\:{b}=\:{c}\:=\:{d} \\ $$$$\:\:\mathrm{then}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\left({a}\:+\:{b}\:+\:{c}\:+\:{d}\right)\:\:=\:\:\sqrt[{\mathrm{4}}]{{abcd}^{} }\: \\ $$$$ \\ $$$$ \\ $$

Commented by Tawa1 last updated on 08/Dec/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by afachri last updated on 08/Dec/18

ur welcome, Sir. Pardon me, are u an Indonesian ?

$$\mathrm{ur}\:\mathrm{welcome},\:\mathrm{Sir}. \\ $$$$\mathrm{Pardon}\:\mathrm{me},\:\mathrm{are}\:\mathrm{u}\:\mathrm{an}\:\mathrm{Indonesian}\:? \\ $$

Commented by Tawa1 last updated on 08/Dec/18

No sir

$$\mathrm{No}\:\mathrm{sir} \\ $$

Commented by afachri last updated on 08/Dec/18

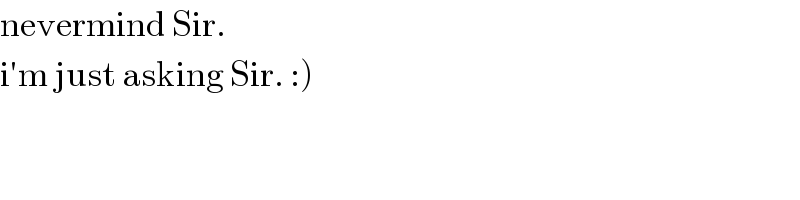
nevermind Sir. i′m just asking Sir. :)

$$\mathrm{nevermind}\:\mathrm{Sir}. \\ $$$$\left.\mathrm{i}'\mathrm{m}\:\mathrm{just}\:\mathrm{asking}\:\mathrm{Sir}.\::\right) \\ $$

Commented by Tawa1 last updated on 08/Dec/18

Ok sir

$$\mathrm{Ok}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 08/Dec/18

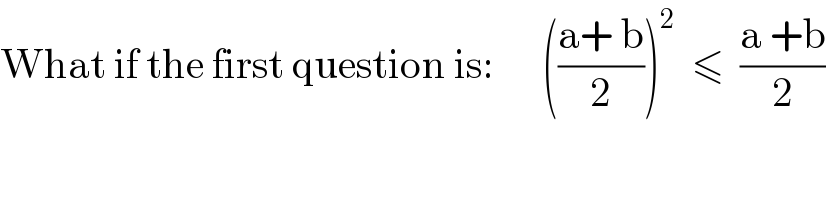
What if the first question is: (((a+ b)/2))^2 ≤ ((a +b)/2)

$$\mathrm{What}\:\mathrm{if}\:\mathrm{the}\:\mathrm{first}\:\mathrm{question}\:\mathrm{is}:\:\:\:\:\:\:\left(\frac{\mathrm{a}+\:\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\leqslant\:\:\frac{\mathrm{a}\:+\mathrm{b}}{\mathrm{2}} \\ $$

Commented by Tawa1 last updated on 08/Dec/18

How will the prove be

$$\mathrm{How}\:\mathrm{will}\:\mathrm{the}\:\mathrm{prove}\:\mathrm{be} \\ $$

Commented by afachri last updated on 08/Dec/18

i had given the 2 solutuions earlier Sir. what kind of proof else you sesrching for Sir ?? i′m sorry i don′t get it.

$$\:\:\mathrm{i}\:\mathrm{had}\:\mathrm{given}\:\mathrm{the}\:\mathrm{2}\:\mathrm{solutuions}\:\mathrm{earlier}\:\mathrm{Sir}. \\ $$$$\:\:\mathrm{what}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{proof}\:\mathrm{else}\:\mathrm{you}\:\mathrm{sesrching} \\ $$$$\:\:\mathrm{for}\:\mathrm{Sir}\:??\:\mathrm{i}'\mathrm{m}\:\mathrm{sorry}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{it}. \\ $$$$ \\ $$

Answered by afachri last updated on 08/Dec/18

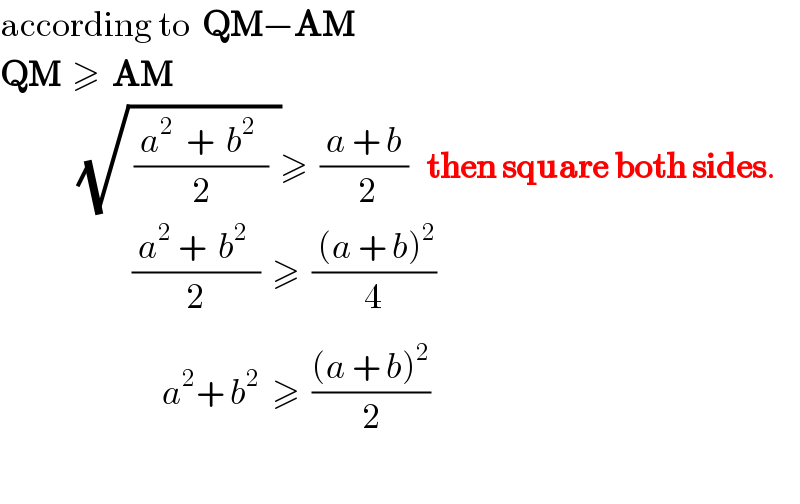
according to QM−AM QM ≥ AM (√( (( a^2^ + b^2 )/2) ))≥ (( a + b )/( 2)) then square both sides. (( a^2 + b^2 )/2) ≥ (( (a + b)^2 )/( 4_ )) a^2 + b^2 ≥ (((a + b)^2 )/2)

$$\mathrm{according}\:\mathrm{to}\:\:\boldsymbol{\mathrm{QM}}−\boldsymbol{\mathrm{AM}} \\ $$$$\boldsymbol{\mathrm{QM}}\:\:\geqslant\:\:\boldsymbol{\mathrm{AM}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\:\frac{\:{a}^{\mathrm{2}^{} } \:+\:\:{b}^{\mathrm{2}} \:\:}{\mathrm{2}}\:\:}\geqslant\:\:\frac{\:{a}\:+\:{b}\:}{\:\mathrm{2}}\:\:\:\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{square}}\:\boldsymbol{\mathrm{both}}\:\boldsymbol{\mathrm{sides}}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\:{a}^{\mathrm{2}} \:+\:\:{b}^{\mathrm{2}} \:\:}{\mathrm{2}}\:\:\geqslant\:\:\frac{\:\left({a}\:+\:{b}\right)^{\mathrm{2}} }{\:\mathrm{4}_{} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\frac{\left({a}\:+\:{b}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 08/Dec/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 08/Dec/18

What is QM and AM sir

$$\mathrm{What}\:\mathrm{is}\:\:\mathrm{QM}\:\mathrm{and}\:\mathrm{AM}\:\mathrm{sir} \\ $$

Commented by afachri last updated on 08/Dec/18

you′re welcome,Sir

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome},\mathrm{Sir} \\ $$

Commented by Tawa1 last updated on 08/Dec/18

???

$$??? \\ $$

Commented by afachri last updated on 08/Dec/18

quadratic mean and arithmaric mean

$$\mathrm{quadratic}\:\mathrm{mean}\:\mathrm{and} \\ $$$$\mathrm{arithmaric}\:\mathrm{mean} \\ $$

Commented by Tawa1 last updated on 08/Dec/18

God bless you sir. I really appreciate your time

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$$$ \\ $$

Commented by afachri last updated on 08/Dec/18

it′s been my pleasure Sir

$$\mathrm{it}'\mathrm{s}\:\mathrm{been}\:\mathrm{my}\:\mathrm{pleasure}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com