
Question Number 4962 by 123456 last updated on 27/Mar/16

$$\mathrm{is}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{proof}\:\mathrm{that} \\ $$$${f}\left({x}\right)={e}^{{cx}} \\ $$$$\mathrm{obey} \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right){f}\left({y}\right) \\ $$$$\mathrm{using} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$$? \\ $$
Commented by 123456 last updated on 27/Mar/16
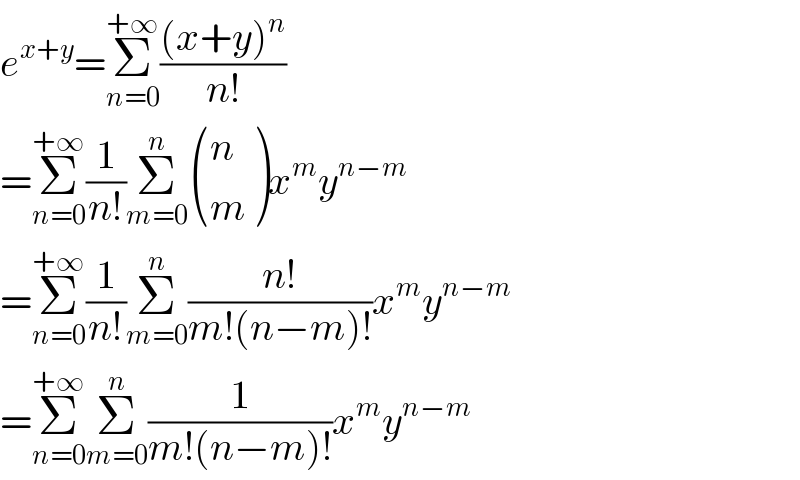
$${e}^{{x}+{y}} =\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\left({x}+{y}\right)^{{n}} }{{n}!} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\underset{{m}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}{x}^{{m}} {y}^{{n}−{m}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\underset{{m}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{{m}!\left({n}−{m}\right)!}{x}^{{m}} {y}^{{n}−{m}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\underset{{m}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{m}!\left({n}−{m}\right)!}{x}^{{m}} {y}^{{n}−{m}} \\ $$
Commented by prakash jain last updated on 08/Jan/17
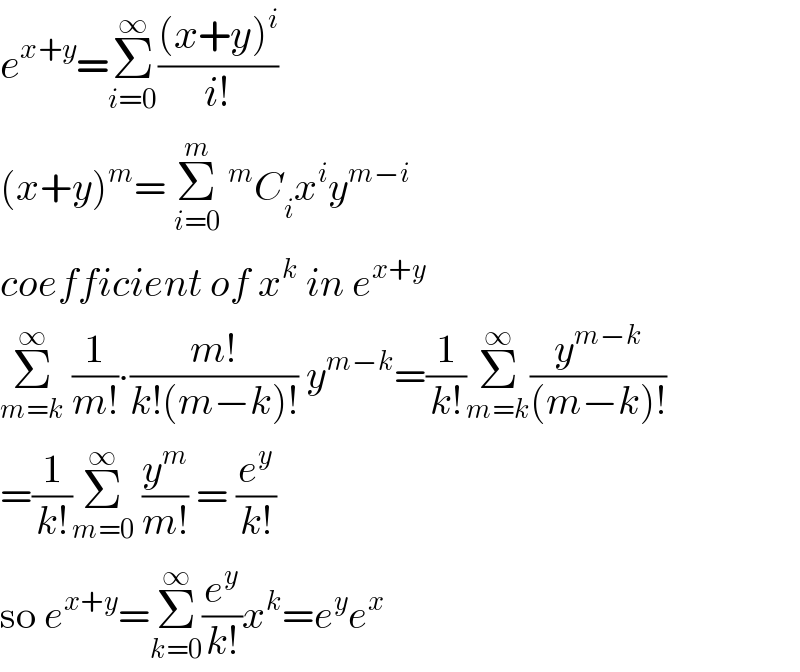
$${e}^{{x}+{y}} =\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({x}+{y}\right)^{{i}} }{{i}!} \\ $$$$\left({x}+{y}\right)^{{m}} =\:\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}\:^{{m}} {C}_{{i}} {x}^{{i}} {y}^{{m}−{i}} \\ $$$${coefficient}\:{of}\:{x}^{{k}} \:{in}\:{e}^{{x}+{y}} \\ $$$$\underset{{m}={k}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{m}!}\centerdot\frac{{m}!}{{k}!\left({m}−{k}\right)!}\:{y}^{{m}−{k}} =\frac{\mathrm{1}}{{k}!}\underset{{m}={k}} {\overset{\infty} {\sum}}\frac{{y}^{{m}−{k}} }{\left({m}−{k}\right)!} \\ $$$$=\frac{\mathrm{1}}{{k}!}\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{y}^{{m}} }{{m}!}\:=\:\frac{{e}^{{y}} }{{k}!} \\ $$$$\mathrm{so}\:{e}^{{x}+{y}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{e}^{{y}} }{{k}!}{x}^{{k}} ={e}^{{y}} {e}^{{x}} \\ $$
