Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 49857 by afachri last updated on 11/Dec/18

Please guide me Sir. I was trying to solve this eq for searching possible values of x. eq is : ∣x − 2∣ < 3∣x + 7∣ the range of x whom i got : −((23)/2) < x < −((19)/4) but the result do not satisfy the eq, instead i put x > −4 , they satisfy the eq. please help me out of this pickle. Not because i didn′t try, yet i always stuck in this type of function.

$$\mathrm{Please}\:\mathrm{guide}\:\mathrm{me}\:\mathrm{Sir}.\:\mathrm{I}\:\mathrm{was}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{solve}\: \\ $$ $$\mathrm{this}\:\mathrm{eq}\:\mathrm{for}\:\mathrm{searching}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:{x}. \\ $$ $$\mathrm{eq}\:\mathrm{is}\:: \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{x}\:−\:\mathrm{2}\mid\:<\:\mathrm{3}\mid{x}\:+\:\mathrm{7}\mid \\ $$ $$\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:{x}\:\mathrm{whom}\:\mathrm{i}\:\mathrm{got}\::\:\:\:−\frac{\mathrm{23}}{\mathrm{2}}\:<\:{x}\:<\:−\frac{\mathrm{19}}{\mathrm{4}} \\ $$ $$\mathrm{but}\:\mathrm{the}\:\mathrm{result}\:\mathrm{do}\:\mathrm{not}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{eq},\:\mathrm{instead} \\ $$ $$\mathrm{i}\:\mathrm{put}\:{x}\:>\:−\mathrm{4}\:,\:\mathrm{they}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{eq}.\: \\ $$ $$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{out}\:\mathrm{of}\:\mathrm{this}\:\mathrm{pickle}. \\ $$ $$\mathrm{Not}\:\mathrm{because}\:\mathrm{i}\:\mathrm{didn}'\mathrm{t}\:\mathrm{try},\:\mathrm{yet}\:\mathrm{i}\:\mathrm{always} \\ $$ $$\mathrm{stuck}\:\mathrm{in}\:\mathrm{this}\:\mathrm{type}\:\mathrm{of}\:\mathrm{function}. \\ $$

Commented bymaxmathsup by imad last updated on 11/Dec/18

the best way is this let A(x)=∣x−2∣−3∣x+7∣ (e) ⇔ A(x)<0 we eradicate the abslutevalue x −∞ −7 2 +∞ ∣x−2∣ −x+2 −x+2 0 x−2 ∣x+7∣ −x−7 0 x+7 x+7 A(x) 2x+23 −4x−19 −2x−23 case 1 x≤−7 (e) ⇔ 2x+23 <0 ⇔ x<−((23)/2) ⇒ S_1 =]−∞ ,−((23)/2)[ case 2 −7≤x≤2 (e) ⇔ −4x −19 <0 ⇔ −4x<19 ⇔4x >−19 ⇔x>−((19)/4) ⇒ S_2 =]−((19)/4) ,2] case 3 x≥2 ⇒ (e)⇔−2x −23 <0 ⇔ −2x<23 ⇔ 2x>−23 ⇔x>−((23)/2) ⇒S_3 =[2,+∞[ and we take ∪S_i S=S_1 ∪S_2 ∪ S_3 =]−∞,−((23)/2)[∪]−((19)/4),+∞[ .

$${the}\:{best}\:{way}\:{is}\:{this}\: \\ $$ $${let}\:{A}\left({x}\right)=\mid{x}−\mathrm{2}\mid−\mathrm{3}\mid{x}+\mathrm{7}\mid\:\:\:\left({e}\right)\:\Leftrightarrow\:{A}\left({x}\right)<\mathrm{0}\:\:{we}\:{eradicate}\:{the}\:{abslutevalue} \\ $$ $${x}\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:−\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$ $$\mid{x}−\mathrm{2}\mid\:\:\:\:\:−{x}+\mathrm{2}\:\:\:−{x}+\mathrm{2}\:\:\mathrm{0}\:\:\:{x}−\mathrm{2} \\ $$ $$\mid{x}+\mathrm{7}\mid\:\:−{x}−\mathrm{7}\:\:\mathrm{0}\:\:\:\:{x}+\mathrm{7}\:\:\:\:\:\:\:\:\:\:{x}+\mathrm{7} \\ $$ $${A}\left({x}\right)\:\:\:\:\mathrm{2}{x}+\mathrm{23}\:\:\:\:\:\:\:−\mathrm{4}{x}−\mathrm{19}\:\:\:\:−\mathrm{2}{x}−\mathrm{23} \\ $$ $$\left.{case}\:\mathrm{1}\:\:\:{x}\leqslant−\mathrm{7}\:\:\:\left({e}\right)\:\Leftrightarrow\:\mathrm{2}{x}+\mathrm{23}\:<\mathrm{0}\:\Leftrightarrow\:{x}<−\frac{\mathrm{23}}{\mathrm{2}}\:\Rightarrow\:{S}_{\mathrm{1}} =\right]−\infty\:,−\frac{\mathrm{23}}{\mathrm{2}}\left[\right. \\ $$ $${case}\:\mathrm{2}\:\:\:\:−\mathrm{7}\leqslant{x}\leqslant\mathrm{2}\:\:\:\:\left({e}\right)\:\Leftrightarrow\:−\mathrm{4}{x}\:−\mathrm{19}\:<\mathrm{0}\:\:\Leftrightarrow\:−\mathrm{4}{x}<\mathrm{19}\:\:\Leftrightarrow\mathrm{4}{x}\:>−\mathrm{19}\:\Leftrightarrow{x}>−\frac{\mathrm{19}}{\mathrm{4}} \\ $$ $$\left.\:\left.\Rightarrow\:{S}_{\mathrm{2}} =\right]−\frac{\mathrm{19}}{\mathrm{4}}\:,\mathrm{2}\right] \\ $$ $${case}\:\mathrm{3}\:\:\:\:\:{x}\geqslant\mathrm{2}\:\Rightarrow\:\left({e}\right)\Leftrightarrow−\mathrm{2}{x}\:−\mathrm{23}\:<\mathrm{0}\:\Leftrightarrow\:−\mathrm{2}{x}<\mathrm{23}\:\Leftrightarrow\:\mathrm{2}{x}>−\mathrm{23}\:\Leftrightarrow{x}>−\frac{\mathrm{23}}{\mathrm{2}} \\ $$ $$\Rightarrow{S}_{\mathrm{3}} =\left[\mathrm{2},+\infty\left[\:\:{and}\:\:{we}\:{take}\:\cup{S}_{{i}} \right.\right. \\ $$ $$\left.{S}={S}_{\mathrm{1}} \cup{S}_{\mathrm{2}} \cup\:{S}_{\mathrm{3}} \:=\right]−\infty,−\frac{\mathrm{23}}{\mathrm{2}}\left[\cup\right]−\frac{\mathrm{19}}{\mathrm{4}},+\infty\left[\:.\right. \\ $$

Commented byafachri last updated on 11/Dec/18

yes it is Sir. Seems this be my another references. thank you Mr Max. soon after Mr Hassen was giving me explanation, i re−tried and get the answer −((23)/2)> x >−((19)/4). and i found match answer to both of yours Sir.

$$\mathrm{yes}\:\mathrm{it}\:\mathrm{is}\:\mathrm{Sir}.\:\mathrm{Seems}\:\mathrm{this}\:\mathrm{be}\:\mathrm{my}\:\mathrm{another}\:\mathrm{references}.\: \\ $$ $$\mathrm{thank}\:\mathrm{you}\:\mathrm{Mr}\:\mathrm{Max}.\:\:\mathrm{soon}\:\mathrm{after}\:\mathrm{Mr}\:\mathrm{Hassen}\:\mathrm{was} \\ $$ $$\mathrm{giving}\:\mathrm{me}\:\mathrm{explanation},\:\mathrm{i}\:\mathrm{re}−\mathrm{tried}\:\mathrm{and}\:\mathrm{get} \\ $$ $$\mathrm{the}\:\mathrm{answer}\:\:−\frac{\mathrm{23}}{\mathrm{2}}>\:{x}\:>−\frac{\mathrm{19}}{\mathrm{4}}.\:\mathrm{and}\:\mathrm{i}\:\mathrm{found} \\ $$ $$\mathrm{match}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{both}\:\mathrm{of}\:\mathrm{yours}\:\mathrm{Sir}.\: \\ $$

Commented byafachri last updated on 11/Dec/18

i′m glad to be part of this forum. Hail Math !

$$\mathrm{i}'\mathrm{m}\:\mathrm{glad}\:\mathrm{to}\:\mathrm{be}\:\mathrm{part}\:\mathrm{of}\:\mathrm{this}\:\mathrm{forum}. \\ $$ $$\mathrm{Hail}\:\mathrm{Math}\:! \\ $$

Commented byAbdo msup. last updated on 12/Dec/18

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Answered by hassentimol last updated on 11/Dec/18

Well... We write it as : ∣x−2∣ − 3∣x+7∣ < 0 We have : { ((x−2 > 0 ⇔ x > 2)),((x+7 > 0 ⇔ x > −7)) :} Therefore we define I_1 , I_2 and I_3 such as : I_1 = ]−∞,−7] : −x+2+3x+21 = 2x+23 I_2 =[−7,2] : −x+2−3x−21 = −4x−19 I_3 =[2,+∞[ : x−2−3x−21 = −2x−23 We have : Let S_n be the set of solutions for the I_n interval. For I_1 : 2x+23<0 ⇔ x<((−23)/2) : S_1 =]−∞,((−23)/2)[ For I_2 : −4x−19<0 ⇔ x>((−19)/4) : S_2 =[((−19)/4),2[ For I_3 : −2x−23<0 ⇔ x>((−23)/2) : S_3 =[2,+∞[ Finally : We can consider S the set of solutions : S = { x ∣ x∈]−∞, ((−19)/4)[ ∪ ]2_ ^ , +∞[ } In other terms : Either x<((−19)/4) , either x>2. Thanks T.H.

$$\mathrm{Well}... \\ $$ $$\mathrm{We}\:\mathrm{write}\:\mathrm{it}\:\mathrm{as}\::\:\:\:\mid{x}−\mathrm{2}\mid\:−\:\mathrm{3}\mid{x}+\mathrm{7}\mid\:<\:\mathrm{0} \\ $$ $$\mathrm{We}\:\mathrm{have}\::\:\begin{cases}{{x}−\mathrm{2}\:>\:\mathrm{0}\:\:\:\Leftrightarrow\:\:\:{x}\:>\:\mathrm{2}}\\{{x}+\mathrm{7}\:>\:\mathrm{0}\:\:\:\Leftrightarrow\:\:\:{x}\:>\:−\mathrm{7}}\end{cases} \\ $$ $$ \\ $$ $$\mathrm{Therefore}\:\mathrm{we}\:\mathrm{define}\:\mathrm{I}_{\mathrm{1}} ,\:\mathrm{I}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{I}_{\mathrm{3}} \:\mathrm{such}\:\mathrm{as}\:: \\ $$ $$\left.\mathrm{I}_{\mathrm{1}} \left.=\:\right]−\infty,−\mathrm{7}\right]\::\:−{x}+\mathrm{2}+\mathrm{3}{x}+\mathrm{21}\:=\:\:\:\mathrm{2}{x}+\mathrm{23} \\ $$ $$\mathrm{I}_{\mathrm{2}} =\left[−\mathrm{7},\mathrm{2}\right]\::\:−{x}+\mathrm{2}−\mathrm{3}{x}−\mathrm{21}\:=\:\:\:−\mathrm{4}{x}−\mathrm{19} \\ $$ $$\mathrm{I}_{\mathrm{3}} =\left[\mathrm{2},+\infty\left[\::\:{x}−\mathrm{2}−\mathrm{3}{x}−\mathrm{21}\:=\:\:\:−\mathrm{2}{x}−\mathrm{23}\right.\right. \\ $$ $$ \\ $$ $$\mathrm{We}\:\mathrm{have}\:: \\ $$ $${Let}\:{S}_{{n}} \:{be}\:{the}\:{set}\:{of}\:{solutions}\:{for}\:{the}\:{I}_{{n}} \:{interval}. \\ $$ $$\left.\mathrm{For}\:\mathrm{I}_{\mathrm{1}} \::\:\mathrm{2}{x}+\mathrm{23}<\mathrm{0}\:\Leftrightarrow\:{x}<\frac{−\mathrm{23}}{\mathrm{2}}\::\:\mathrm{S}_{\mathrm{1}} =\right]−\infty,\frac{−\mathrm{23}}{\mathrm{2}}\left[\right. \\ $$ $$\mathrm{For}\:\mathrm{I}_{\mathrm{2}} \::\:−\mathrm{4}{x}−\mathrm{19}<\mathrm{0}\:\Leftrightarrow\:{x}>\frac{−\mathrm{19}}{\mathrm{4}}\::\:\mathrm{S}_{\mathrm{2}} =\left[\frac{−\mathrm{19}}{\mathrm{4}},\mathrm{2}\left[\right.\right. \\ $$ $$\mathrm{For}\:\mathrm{I}_{\mathrm{3}} \::\:−\mathrm{2}{x}−\mathrm{23}<\mathrm{0}\:\Leftrightarrow\:{x}>\frac{−\mathrm{23}}{\mathrm{2}}\::\:\mathrm{S}_{\mathrm{3}} =\left[\mathrm{2},+\infty\left[\right.\right. \\ $$ $$ \\ $$ $$\mathrm{Finally}\:: \\ $$ $$ \\ $$ $$\mathrm{We}\:\mathrm{can}\:\mathrm{consider}\:\mathbb{S}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{solutions}\:: \\ $$ $$\:\:\:\:\mathbb{S}\:=\:\left\{\:{x}\:\mid\:{x}\in\right]−\infty,\:\frac{−\mathrm{19}}{\mathrm{4}}\left[\:\cup\:\right]\underset{} {\overset{} {\mathrm{2}}},\:+\infty\left[\:\right\} \\ $$ $$ \\ $$ $$\mathrm{In}\:\mathrm{other}\:\mathrm{terms}\:: \\ $$ $$\mathrm{Either}\:{x}<\frac{−\mathrm{19}}{\mathrm{4}}\:,\:\mathrm{either}\:{x}>\mathrm{2}. \\ $$ $$ \\ $$ $$\boldsymbol{{Thanks}} \\ $$ $$\boldsymbol{{T}}.\boldsymbol{{H}}. \\ $$

Commented byafachri last updated on 11/Dec/18

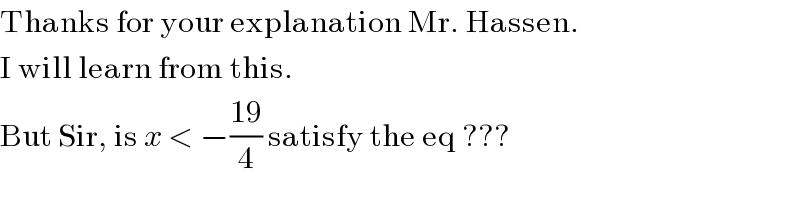
Thanks for your explanation Mr. Hassen. I will learn from this. But Sir, is x < −((19)/4) satisfy the eq ???

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{explanation}\:\mathrm{Mr}.\:\mathrm{Hassen}. \\ $$ $$\mathrm{I}\:\mathrm{will}\:\mathrm{learn}\:\mathrm{from}\:\mathrm{this}. \\ $$ $$\mathrm{But}\:\mathrm{Sir},\:\mathrm{is}\:{x}\:<\:−\frac{\mathrm{19}}{\mathrm{4}}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{eq}\:??? \\ $$

Commented byhassentimol last updated on 11/Dec/18

You are welcome sir. It was a pleasure.

$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}.\:\mathrm{It}\:\mathrm{was}\:\mathrm{a}\:\mathrm{pleasure}. \\ $$

Commented byhassentimol last updated on 11/Dec/18

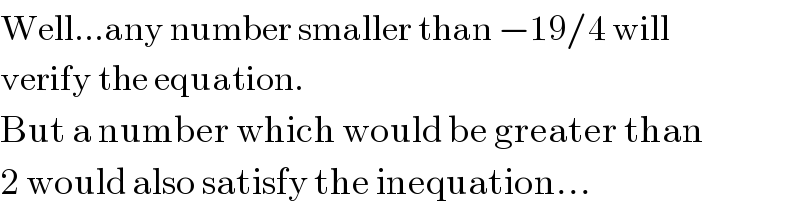
Well...any number smaller than −19/4 will verify the equation. But a number which would be greater than 2 would also satisfy the inequation...

$$\mathrm{Well}...\mathrm{any}\:\mathrm{number}\:\mathrm{smaller}\:\mathrm{than}\:−\mathrm{19}/\mathrm{4}\:\mathrm{will} \\ $$ $$\mathrm{verify}\:\mathrm{the}\:\mathrm{equation}. \\ $$ $$\mathrm{But}\:\mathrm{a}\:\mathrm{number}\:\mathrm{which}\:\mathrm{would}\:\mathrm{be}\:\mathrm{greater}\:\mathrm{than} \\ $$ $$\mathrm{2}\:\mathrm{would}\:\mathrm{also}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{inequation}... \\ $$

Commented byhassentimol last updated on 11/Dec/18

Commented byhassentimol last updated on 11/Dec/18

This is the curve of the function when all is put on one side of the inequation. The solutions are when the curve is negative...

$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{when}\:\mathrm{all}\:\mathrm{is}\:\mathrm{put} \\ $$ $$\mathrm{on}\:\mathrm{one}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{inequation}. \\ $$ $$\mathrm{The}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{when}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{is}\:\mathrm{negative}... \\ $$

Commented byafachri last updated on 11/Dec/18

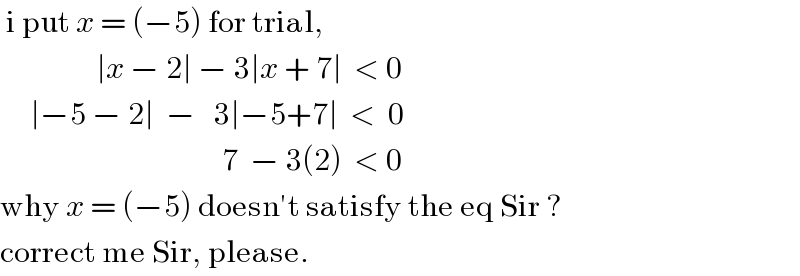
i put x = (−5) for trial, ∣x − 2∣ − 3∣x + 7∣ < 0 ∣−5 − 2∣ − 3∣−5+7∣ < 0 7 − 3(2) < 0 why x = (−5) doesn′t satisfy the eq Sir ? correct me Sir, please.

$$\:\mathrm{i}\:\mathrm{put}\:{x}\:=\:\left(−\mathrm{5}\right)\:\mathrm{for}\:\mathrm{trial},\: \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{x}\:−\:\mathrm{2}\mid\:−\:\mathrm{3}\mid{x}\:+\:\mathrm{7}\mid\:\:<\:\mathrm{0} \\ $$ $$\:\:\:\:\:\mid−\mathrm{5}\:−\:\mathrm{2}\mid\:\:−\:\:\:\mathrm{3}\mid−\mathrm{5}+\mathrm{7}\mid\:\:<\:\:\mathrm{0} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}\:\:−\:\mathrm{3}\left(\mathrm{2}\right)\:\:<\:\mathrm{0}\: \\ $$ $$\mathrm{why}\:{x}\:=\:\left(−\mathrm{5}\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{eq}\:\mathrm{Sir}\:? \\ $$ $$\mathrm{correct}\:\mathrm{me}\:\mathrm{Sir},\:\mathrm{please}. \\ $$

Commented byafachri last updated on 11/Dec/18

Commented byafachri last updated on 11/Dec/18

thank you very much Sir. i′ve looked in my graphic too and understand now. :)

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}.\:\mathrm{i}'\mathrm{ve}\:\mathrm{looked}\:\mathrm{in} \\ $$ $$\mathrm{my}\:\mathrm{graphic}\:\mathrm{too}\:\mathrm{and}\:\mathrm{understand}\:\mathrm{now}. \\ $$ $$\left.:\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com