Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 50048 by ajfour last updated on 13/Dec/18

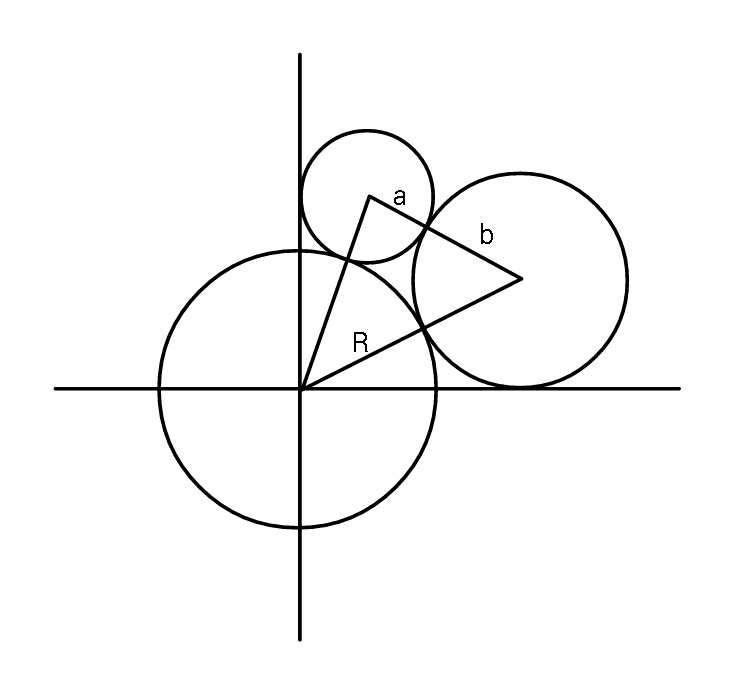
Commented by ajfour last updated on 13/Dec/18

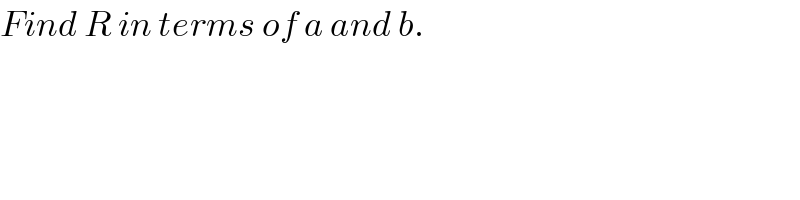
Find R in terms of a and b.

$${Find}\:{R}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$

Commented by ajfour last updated on 13/Dec/18

Commented by MJS last updated on 14/Dec/18

the problem can be seen as follows: 2 circles are given with radii a and b, they have exactly 1 common point we′re looking (1) for a 3^(rd) circle touching both in exactly 1 common point each, with radius R we′re looking (2) for pairs of tangents to circles a and b which include a right angle the goal is to find R and the tangents meeting in the center of the 3^(rd) circle we can put the circles as follows: (x−a)^2 +y^2 =a^2 ; a<0 (x−b)^2 +y^2 =b^2 ; b>0 (x−p)^2 +(y−q)^2 =R^2 ⇒ p=((a+b)/(a−b))R; q=−(2/(a−b))(√(abR(a−b−R))) we need the upper half circles for the tangents. let x=u for circle a and x=v for circle b ⇒ tangent at x=v normal to tangent in x=u ⇔ v=b−(b/a)(√(2au−u^2 )) the tangents then intersect at ((m),(n) ) with m=((a−b)/a^2 )u^2 +((2b−a)/a)u−(b/a)(√(2au−u^2 )) n=(b/a)u−b+(((a−b)u+ab)/a^2 )(√(2au−u^2 )) now we have the system p=m q=n which must be solved for u and R but it leads to a polynome of 8^(th) degree...

$$\mathrm{the}\:\mathrm{problem}\:\mathrm{can}\:\mathrm{be}\:\mathrm{seen}\:\mathrm{as}\:\mathrm{follows}: \\ $$$$\mathrm{2}\:\mathrm{circles}\:\mathrm{are}\:\mathrm{given}\:\mathrm{with}\:\mathrm{radii}\:{a}\:\mathrm{and}\:{b},\:\mathrm{they} \\ $$$$\mathrm{have}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{common}\:\mathrm{point} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\left(\mathrm{1}\right)\:\mathrm{for}\:\mathrm{a}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{circle}\:\mathrm{touching}\:\mathrm{both} \\ $$$$\mathrm{in}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{common}\:\mathrm{point}\:\mathrm{each},\:\mathrm{with}\:\mathrm{radius}\:{R} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\left(\mathrm{2}\right)\:\mathrm{for}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{tangents}\:\mathrm{to} \\ $$$$\mathrm{circles}\:{a}\:\mathrm{and}\:{b}\:\mathrm{which}\:\mathrm{include}\:\mathrm{a}\:\mathrm{right}\:\mathrm{angle} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{goal}\:\mathrm{is}\:\mathrm{to}\:\mathrm{find}\:{R}\:\mathrm{and}\:\mathrm{the}\:\mathrm{tangents}\:\mathrm{meeting} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{circle} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{put}\:\mathrm{the}\:\mathrm{circles}\:\mathrm{as}\:\mathrm{follows}: \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} ;\:{a}<\mathrm{0} \\ $$$$\left({x}−{b}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} ;\:{b}>\mathrm{0} \\ $$$$\left({x}−{p}\right)^{\mathrm{2}} +\left({y}−{q}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\:{p}=\frac{{a}+{b}}{{a}−{b}}{R};\:{q}=−\frac{\mathrm{2}}{{a}−{b}}\sqrt{{abR}\left({a}−{b}−{R}\right)} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{half}\:\mathrm{circles}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{tangents}.\:\mathrm{let}\:{x}={u}\:\mathrm{for}\:\mathrm{circle}\:{a}\:\mathrm{and}\:{x}={v}\:\mathrm{for} \\ $$$$\mathrm{circle}\:{b}\:\Rightarrow\:\mathrm{tangent}\:\mathrm{at}\:{x}={v}\:\mathrm{normal}\:\mathrm{to}\:\mathrm{tangent} \\ $$$$\mathrm{in}\:{x}={u}\:\Leftrightarrow\:{v}={b}−\frac{{b}}{{a}}\sqrt{\mathrm{2}{au}−{u}^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{tangents}\:\mathrm{then}\:\mathrm{intersect}\:\mathrm{at}\:\begin{pmatrix}{{m}}\\{{n}}\end{pmatrix}\:\mathrm{with} \\ $$$${m}=\frac{{a}−{b}}{{a}^{\mathrm{2}} }{u}^{\mathrm{2}} +\frac{\mathrm{2}{b}−{a}}{{a}}{u}−\frac{{b}}{{a}}\sqrt{\mathrm{2}{au}−{u}^{\mathrm{2}} } \\ $$$${n}=\frac{{b}}{{a}}{u}−{b}+\frac{\left({a}−{b}\right){u}+{ab}}{{a}^{\mathrm{2}} }\sqrt{\mathrm{2}{au}−{u}^{\mathrm{2}} } \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{system} \\ $$$${p}={m} \\ $$$${q}={n} \\ $$$$\mathrm{which}\:\mathrm{must}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:{u}\:\mathrm{and}\:{R} \\ $$$$\mathrm{but}\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{8}^{\mathrm{th}} \:\mathrm{degree}... \\ $$

Commented by ajfour last updated on 14/Dec/18

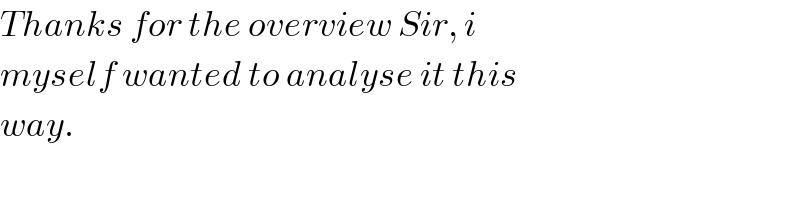
Thanks for the overview Sir, i myself wanted to analyse it this way.

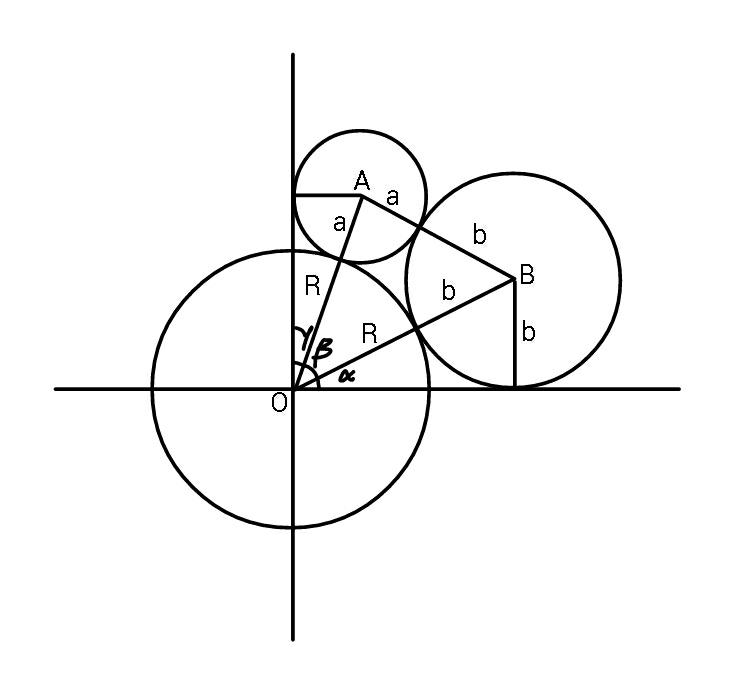
$${Thanks}\:{for}\:{the}\:{overview}\:{Sir},\:{i} \\ $$$${myself}\:{wanted}\:{to}\:{analyse}\:{it}\:{this} \\ $$$${way}. \\ $$

Answered by behi83417@gmail.com last updated on 13/Dec/18

cosα=((√((R+b)^2 −b^2 ))/(R+b))=((√(R^2 +2Rb))/(R+b))=((√(1+2n))/(1+n)) cosγ=((√((R+a)^2 −a^2 ))/(R+a))=((√(R^2 +2Ra))/(R+a))=((√(1+2m))/(1+m)) sinα=(b/(R+b))=(n/(1+n)),sinγ=(a/(R+a))=(m/(1+m)) (a/R)=m,(b/R)=n sin(α+γ)=((m(√(1+2n))+n(√(1+2m)))/((1+m)(1+n))) =((s(t^2 −1)+t(s^2 −1))/(4(1+((t^2 −1)/2))(1+((s^2 −1)/2))))=(((st−1)(s+t))/((s^2 +1)(t^2 +1))) [1+2m=t^2 ,1+2n=s^2 ⇒m=((t^2 −1)/2),n=((s^2 −1)/2)] β=90−(α+γ)⇒cosβ=sin(α+γ) (a+b)^2 =(R+a)^2 +(R+b)^2 −2(R+a)(R+b).cosβ⇒ (m+n)^2 =[(1+m)^2 +(1+n)^2 −2(m(√(1+2n))+n(√(1+2m)))] (((t^2 +s^2 −2)/2))^2 =[(((t^2 +1)/2))^2 +(((s^2 +1)/2))^2 −2(((t^2 −1)/2)s+((s^2 −1)/2)t)] (t^2 +s^2 −2)^2 =(t^2 +1)^2 +(s^2 +1)^2 −4(st^2 +ts^2 −s−t) t^4 +s^4 +4−4t^2 −4s^2 +2t^2 s^2 = t^4 +2t^2 +1+s^4 +2s^2 +1−4st^2 −4ts^2 +4s+4t 3t^2 +3s^2 −t^2 s^2 −2st^2 −2ts^2 +2s+2t=0 (s^2 +2s−3)t^2 +2(s^2 −1)t−(3s^2 +2s)=0 △′=b′^2 −ac=(s^2 −1)^2 +(s^2 +2s−3)(3s^2 +2s)= =s^4 −2s^2 +1+3s^4 +2s^3 +6s^3 +4s^2 −9s^2 −6s= =4s^4 +8s^3 −7s^2 −6s+1 =(s−1)[4s^3 +12s^2 +5s−1] t=(((1−s^2 )±(√(4s^4 +8s^3 −7s^2 −6s+1)))/(s^2 +2s−3)) .....

$${cos}\alpha=\frac{\sqrt{\left({R}+{b}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }}{{R}+{b}}=\frac{\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Rb}}}{{R}+{b}}=\frac{\sqrt{\mathrm{1}+\mathrm{2}{n}}}{\mathrm{1}+{n}} \\ $$$${cos}\gamma=\frac{\sqrt{\left({R}+{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{R}+{a}}=\frac{\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Ra}}}{{R}+{a}}=\frac{\sqrt{\mathrm{1}+\mathrm{2}{m}}}{\mathrm{1}+{m}} \\ $$$${sin}\alpha=\frac{{b}}{{R}+{b}}=\frac{{n}}{\mathrm{1}+{n}},{sin}\gamma=\frac{{a}}{{R}+{a}}=\frac{{m}}{\mathrm{1}+{m}} \\ $$$$\frac{{a}}{{R}}={m},\frac{{b}}{{R}}={n} \\ $$$${sin}\left(\alpha+\gamma\right)=\frac{{m}\sqrt{\mathrm{1}+\mathrm{2}{n}}+{n}\sqrt{\mathrm{1}+\mathrm{2}{m}}}{\left(\mathrm{1}+{m}\right)\left(\mathrm{1}+{n}\right)} \\ $$$$=\frac{{s}\left({t}^{\mathrm{2}} −\mathrm{1}\right)+{t}\left({s}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{4}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{{s}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right)}=\frac{\left({st}−\mathrm{1}\right)\left({s}+{t}\right)}{\left({s}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\left[\mathrm{1}+\mathrm{2}{m}={t}^{\mathrm{2}} ,\mathrm{1}+\mathrm{2}{n}={s}^{\mathrm{2}} \Rightarrow{m}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}},{n}=\frac{{s}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right] \\ $$$$\beta=\mathrm{90}−\left(\alpha+\gamma\right)\Rightarrow{cos}\beta={sin}\left(\alpha+\gamma\right) \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} =\left({R}+{a}\right)^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} −\mathrm{2}\left({R}+{a}\right)\left({R}+{b}\right).{cos}\beta\Rightarrow \\ $$$$\left({m}+{n}\right)^{\mathrm{2}} =\left[\left(\mathrm{1}+{m}\right)^{\mathrm{2}} +\left(\mathrm{1}+{n}\right)^{\mathrm{2}} −\mathrm{2}\left({m}\sqrt{\mathrm{1}+\mathrm{2}{n}}+{n}\sqrt{\mathrm{1}+\mathrm{2}{m}}\right)\right] \\ $$$$\left(\frac{{t}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}}\right)^{\mathrm{2}} =\left[\left(\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{s}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}{s}+\frac{{s}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}{t}\right)\right] \\ $$$$\left({t}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} =\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\left({s}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left({st}^{\mathrm{2}} +{ts}^{\mathrm{2}} −{s}−{t}\right) \\ $$$${t}^{\mathrm{4}} +{s}^{\mathrm{4}} +\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{s}^{\mathrm{2}} +\mathrm{2}{t}^{\mathrm{2}} {s}^{\mathrm{2}} = \\ $$$${t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}+{s}^{\mathrm{4}} +\mathrm{2}{s}^{\mathrm{2}} +\mathrm{1}−\mathrm{4}{st}^{\mathrm{2}} −\mathrm{4}{ts}^{\mathrm{2}} +\mathrm{4}{s}+\mathrm{4}{t} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{s}^{\mathrm{2}} −{t}^{\mathrm{2}} {s}^{\mathrm{2}} −\mathrm{2}{st}^{\mathrm{2}} −\mathrm{2}{ts}^{\mathrm{2}} +\mathrm{2}{s}+\mathrm{2}{t}=\mathrm{0} \\ $$$$\left({s}^{\mathrm{2}} +\mathrm{2}{s}−\mathrm{3}\right){t}^{\mathrm{2}} +\mathrm{2}\left({s}^{\mathrm{2}} −\mathrm{1}\right){t}−\left(\mathrm{3}{s}^{\mathrm{2}} +\mathrm{2}{s}\right)=\mathrm{0} \\ $$$$\bigtriangleup'={b}'^{\mathrm{2}} −{ac}=\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\left({s}^{\mathrm{2}} +\mathrm{2}{s}−\mathrm{3}\right)\left(\mathrm{3}{s}^{\mathrm{2}} +\mathrm{2}{s}\right)= \\ $$$$={s}^{\mathrm{4}} −\mathrm{2}{s}^{\mathrm{2}} +\mathrm{1}+\mathrm{3}{s}^{\mathrm{4}} +\mathrm{2}{s}^{\mathrm{3}} +\mathrm{6}{s}^{\mathrm{3}} +\mathrm{4}{s}^{\mathrm{2}} −\mathrm{9}{s}^{\mathrm{2}} −\mathrm{6}{s}= \\ $$$$=\mathrm{4}{s}^{\mathrm{4}} +\mathrm{8}{s}^{\mathrm{3}} −\mathrm{7}{s}^{\mathrm{2}} −\mathrm{6}{s}+\mathrm{1} \\ $$$$=\left({s}−\mathrm{1}\right)\left[\mathrm{4}{s}^{\mathrm{3}} +\mathrm{12}{s}^{\mathrm{2}} +\mathrm{5}{s}−\mathrm{1}\right] \\ $$$${t}=\frac{\left(\mathrm{1}−{s}^{\mathrm{2}} \right)\pm\sqrt{\mathrm{4}{s}^{\mathrm{4}} +\mathrm{8}{s}^{\mathrm{3}} −\mathrm{7}{s}^{\mathrm{2}} −\mathrm{6}{s}+\mathrm{1}}}{{s}^{\mathrm{2}} +\mathrm{2}{s}−\mathrm{3}} \\ $$$$..... \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 13/Dec/18

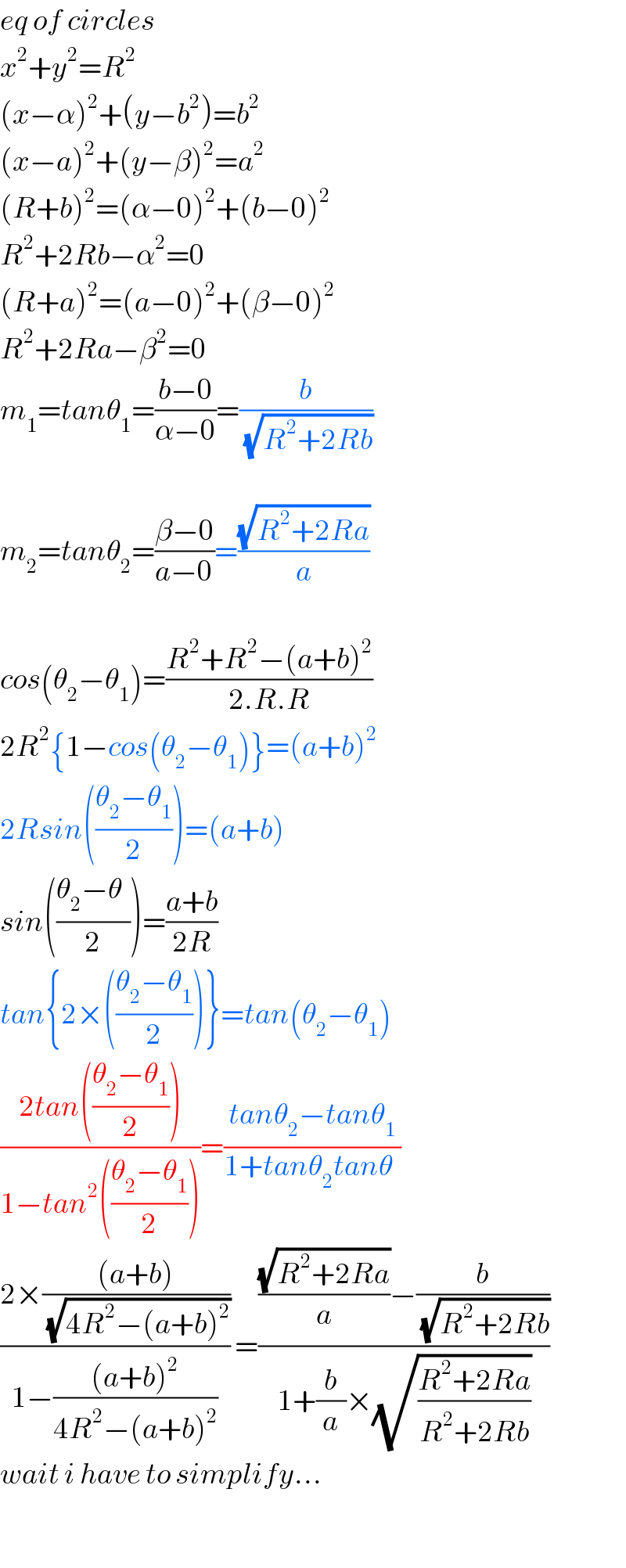
eq of circles x^2 +y^2 =R^2 (x−α)^2 +(y−b^2 )=b^2 (x−a)^2 +(y−β)^2 =a^2 (R+b)^2 =(α−0)^2 +(b−0)^2 R^2 +2Rb−α^2 =0 (R+a)^2 =(a−0)^2 +(β−0)^2 R^2 +2Ra−β^2 =0 m_1 =tanθ_1 =((b−0)/(α−0))=(b/(√(R^2 +2Rb))) m_2 =tanθ_2 =((β−0)/(a−0))=((√(R^2 +2Ra))/a) cos(θ_2 −θ_1 )=((R^2 +R^2 −(a+b)^2 )/(2.R.R)) 2R^2 {1−cos(θ_2 −θ_1 )}=(a+b)^2 2Rsin(((θ_2 −θ_1 )/2))=(a+b) sin(((θ_2 −θ_ )/2))=((a+b)/(2R)) tan{2×(((θ_2 −θ_1 )/2))}=tan(θ_2 −θ_1 ) ((2tan(((θ_2 −θ_1 )/2)))/(1−tan^2 (((θ_2 −θ_1 )/2))))=((tanθ_2 −tanθ_1 )/(1+tanθ_2 tanθ_ )) ((2×(((a+b))/(√(4R^2 −(a+b)^2 ))))/(1−(((a+b)^2 )/(4R^2 −(a+b)^2 )))) =((((√(R^2 +2Ra))/a)−(b/(√(R^2 +2Rb))))/(1+(b/a)×(√((R^2 +2Ra)/(R^2 +2Rb))))) wait i have to simplify...

$${eq}\:{of}\:{circles} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\left({x}−\alpha\right)^{\mathrm{2}} +\left({y}−{b}^{\mathrm{2}} \right)={b}^{\mathrm{2}} \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−\beta\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left({R}+{b}\right)^{\mathrm{2}} =\left(\alpha−\mathrm{0}\right)^{\mathrm{2}} +\left({b}−\mathrm{0}\right)^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} +\mathrm{2}{Rb}−\alpha^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({R}+{a}\right)^{\mathrm{2}} =\left({a}−\mathrm{0}\right)^{\mathrm{2}} +\left(\beta−\mathrm{0}\right)^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} +\mathrm{2}{Ra}−\beta^{\mathrm{2}} =\mathrm{0} \\ $$$${m}_{\mathrm{1}} ={tan}\theta_{\mathrm{1}} =\frac{{b}−\mathrm{0}}{\alpha−\mathrm{0}}=\frac{{b}}{\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Rb}}} \\ $$$$ \\ $$$${m}_{\mathrm{2}} ={tan}\theta_{\mathrm{2}} =\frac{\beta−\mathrm{0}}{{a}−\mathrm{0}}=\frac{\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Ra}}}{{a}} \\ $$$$ \\ $$$${cos}\left(\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \right)=\frac{{R}^{\mathrm{2}} +{R}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}.{R}.{R}} \\ $$$$\mathrm{2}{R}^{\mathrm{2}} \left\{\mathrm{1}−{cos}\left(\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \right)\right\}=\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{Rsin}\left(\frac{\theta_{\mathrm{2}} −\theta_{\mathrm{1}} }{\mathrm{2}}\right)=\left({a}+{b}\right) \\ $$$${sin}\left(\frac{\theta_{\mathrm{2}} −\theta_{} }{\mathrm{2}}\right)=\frac{{a}+{b}}{\mathrm{2}{R}} \\ $$$${tan}\left\{\mathrm{2}×\left(\frac{\theta_{\mathrm{2}} −\theta_{\mathrm{1}} }{\mathrm{2}}\right)\right\}={tan}\left(\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \right) \\ $$$$\frac{\mathrm{2}{tan}\left(\frac{\theta_{\mathrm{2}} −\theta_{\mathrm{1}} }{\mathrm{2}}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{\theta_{\mathrm{2}} −\theta_{\mathrm{1}} }{\mathrm{2}}\right)}=\frac{{tan}\theta_{\mathrm{2}} −{tan}\theta_{\mathrm{1}} }{\mathrm{1}+{tan}\theta_{\mathrm{2}} {tan}\theta_{} } \\ $$$$\frac{\mathrm{2}×\frac{\left({a}+{b}\right)}{\sqrt{\mathrm{4}{R}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }}}{\mathrm{1}−\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }}\:=\frac{\frac{\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Ra}}}{{a}}−\frac{{b}}{\sqrt{{R}^{\mathrm{2}} +\mathrm{2}{Rb}}}}{\mathrm{1}+\frac{{b}}{{a}}×\sqrt{\frac{{R}^{\mathrm{2}} +\mathrm{2}{Ra}}{{R}^{\mathrm{2}} +\mathrm{2}{Rb}}}} \\ $$$${wait}\:{i}\:{have}\:{to}\:{simplify}... \\ $$$$ \\ $$

Answered by ajfour last updated on 13/Dec/18

let (b/R) = s, (a/R) = t sin α = (b/(R+b)) = (s/(1+s)) sin γ = (a/(R+a)) = (t/(1+t)) cos β = (((R+a)^2 +(R+b)^2 −(a+b)^2 )/(2(R+a)(R+b))) = (((1+t)^2 +(1+s)^2 −(t+s)^2 )/(2(1+t)(1+s))) = ((1+t+s−st)/(1+t+s+st)) cos β = sin (α+γ) ⇒ ((1+t+s−st)/(1+t+s+st)) = (s/(1+s))×((√(1+2t))/(1+t))+(t/(1+t))×((√(1+2s))/(1+s)) ⇒ 1+s+t−st = s(√(1+2t))+t(√(1+2s)) ⇒ 1+(b/R)+(a/R)−((ab)/R^2 ) = (b/R)(√(1+((2a)/R))) +(a/R)(√(1+((2b)/R))) R^2 +(a+b)R−ab = (√R)(b(√(R+2a))+a(√(R+2b)) ) let (R/b) = x , (a/b) = c ⇒ x^2 +(c+1)x−c = (√x) ((√(x+2c))+c(√(x+2)) ) ⇒ i cannot solve it .

$${let}\:\frac{{b}}{{R}}\:=\:{s},\:\:\frac{{a}}{{R}}\:=\:{t} \\ $$$$\mathrm{sin}\:\alpha\:=\:\frac{{b}}{{R}+{b}}\:=\:\frac{{s}}{\mathrm{1}+{s}} \\ $$$$\mathrm{sin}\:\gamma\:=\:\frac{{a}}{{R}+{a}}\:=\:\frac{{t}}{\mathrm{1}+{t}} \\ $$$$\mathrm{cos}\:\beta\:=\:\frac{\left({R}+{a}\right)^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}+{a}\right)\left({R}+{b}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +\left(\mathrm{1}+{s}\right)^{\mathrm{2}} −\left({t}+{s}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{s}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}+{t}+{s}−{st}}{\mathrm{1}+{t}+{s}+{st}} \\ $$$$\mathrm{cos}\:\beta\:=\:\mathrm{sin}\:\left(\alpha+\gamma\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}+{t}+{s}−{st}}{\mathrm{1}+{t}+{s}+{st}}\:=\:\frac{{s}}{\mathrm{1}+{s}}×\frac{\sqrt{\mathrm{1}+\mathrm{2}{t}}}{\mathrm{1}+{t}}+\frac{{t}}{\mathrm{1}+{t}}×\frac{\sqrt{\mathrm{1}+\mathrm{2}{s}}}{\mathrm{1}+{s}} \\ $$$$\Rightarrow\:\mathrm{1}+{s}+{t}−{st}\:=\:{s}\sqrt{\mathrm{1}+\mathrm{2}{t}}+{t}\sqrt{\mathrm{1}+\mathrm{2}{s}} \\ $$$$\Rightarrow\:\:\mathrm{1}+\frac{{b}}{{R}}+\frac{{a}}{{R}}−\frac{{ab}}{{R}^{\mathrm{2}} }\:=\:\frac{{b}}{{R}}\sqrt{\mathrm{1}+\frac{\mathrm{2}{a}}{{R}}}\:+\frac{{a}}{{R}}\sqrt{\mathrm{1}+\frac{\mathrm{2}{b}}{{R}}} \\ $$$${R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}\:=\:\sqrt{{R}}\left({b}\sqrt{{R}+\mathrm{2}{a}}+{a}\sqrt{{R}+\mathrm{2}{b}}\:\right) \\ $$$${let}\:\:\frac{{R}}{{b}}\:=\:{x}\:,\:\:\frac{{a}}{{b}}\:=\:{c}\:\:\Rightarrow \\ $$$${x}^{\mathrm{2}} +\left({c}+\mathrm{1}\right){x}−{c}\:=\:\sqrt{{x}}\:\left(\sqrt{{x}+\mathrm{2}{c}}+{c}\sqrt{{x}+\mathrm{2}}\:\right) \\ $$$$\Rightarrow\:{i}\:{cannot}\:{solve}\:{it}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com