
Question Number 50406 by Abdo msup. last updated on 16/Dec/18
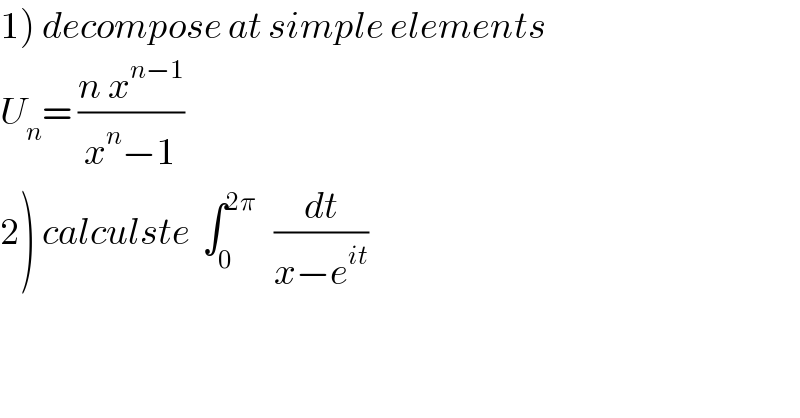
$$\left.\mathrm{1}\right)\:{decompose}\:{at}\:{simple}\:{elements} \\ $$$${U}_{{n}} =\:\frac{{n}\:{x}^{{n}−\mathrm{1}} }{{x}^{{n}} −\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{calculste}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{x}−{e}^{{it}} } \\ $$
Commented by Abdo msup. last updated on 25/Dec/18
![let p(x)=x^n −1 the roots of p(x) are z_k =e^(i((2kπ)/n)) with k∈[[0,n−1]] but U_n =Σ_(k=0) ^(n−1) (λ_k /(x−z_k )) λ_k =((nz_k ^(n−1) )/(p^′ (z_k ))) =(n/z_k ) (1/(n z_k ^(n−1) )) =1 ⇒ U_n =Σ_(k=0) ^(n−1) (1/(x−z_k )) =Σ_(k=0) ^(n−1) (1/(x−e^(i((2kπ)/n)) ))](Q51319.png)
$${let}\:{p}\left({x}\right)={x}^{{n}} −\mathrm{1}\:\:{the}\:{roots}\:{of}\:{p}\left({x}\right)\:{are}\:{z}_{{k}} ={e}^{{i}\frac{\mathrm{2}{k}\pi}{{n}}} \\ $$$${with}\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\:{but}\:{U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\lambda_{{k}} }{{x}−{z}_{{k}} } \\ $$$$\lambda_{{k}} =\frac{{nz}_{{k}} ^{{n}−\mathrm{1}} }{{p}^{'} \left({z}_{{k}} \right)}\:=\frac{{n}}{{z}_{{k}} }\:\frac{\mathrm{1}}{{n}\:{z}_{{k}} ^{{n}−\mathrm{1}} }\:=\mathrm{1}\:\Rightarrow\:{U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\mathrm{1}}{{x}−{z}_{{k}} } \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\mathrm{1}}{{x}−{e}^{{i}\frac{\mathrm{2}{k}\pi}{{n}}} } \\ $$
Commented by Abdo msup. last updated on 25/Dec/18
![2) changement e^(it) =z give ∫_0 ^(2π) (dt/(x−e^(it) )) =∫_(∣z∣=1) (1/(x−z)) (dz/(iz)) =∫_(∣z∣=1) ((−idz)/(xz −z^2 )) =∫_(∣z∣=1) ((idz)/(z^2 −xz)) let ϕ(z) =(i/(z^2 −xz)) =(i/(z(z−x))) so the polesx of ϕ are 0 and x if ∣x∣<1 ∫_(∣z∣=1) ϕ(z)dz =2iπ(Res(ϕ,0)+Res(ϕ,x)} Res(ϕ,0) =lim_(z→0) zϕ(z)=−(i/x) Res(ϕ,x) =lim_(z→x) (z−x)ϕ(z)=(i/x)⇒ ∫_(∣z∣=1) ϕ(z)dz =0 if ∣x∣>1 ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,0) =2iπ(((−i)/x)) =((2π)/x) (we suppose x≠0) if x=0 ∫_0 ^(2π) (dt/(x−e^(it) )) =−∫_0 ^(2π) e^(−it) dt =−[−(1/i) e^(−it) ]_0 ^(2π) =(1/i)(1−1)=0](Q51323.png)
$$\left.\mathrm{2}\right)\:{changement}\:{e}^{{it}} ={z}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{x}−{e}^{{it}} }\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{{x}−{z}}\:\frac{{dz}}{{iz}} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\frac{−{idz}}{{xz}\:−{z}^{\mathrm{2}} }\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{{idz}}{{z}^{\mathrm{2}} −{xz}}\:\:{let} \\ $$$$\varphi\left({z}\right)\:=\frac{{i}}{{z}^{\mathrm{2}} −{xz}}\:=\frac{{i}}{{z}\left({z}−{x}\right)}\:{so}\:{the}\:{polesx}\:{of}\:\varphi\:{are}\:\mathrm{0}\:{and} \\ $$$${x}\:\:\:{if}\:\mid{x}\mid<\mathrm{1}\:\:\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left({Res}\left(\varphi,\mathrm{0}\right)+{Res}\left(\varphi,{x}\right)\right\} \\ $$$${Res}\left(\varphi,\mathrm{0}\right)\:={lim}_{{z}\rightarrow\mathrm{0}} {z}\varphi\left({z}\right)=−\frac{{i}}{{x}} \\ $$$${Res}\left(\varphi,{x}\right)\:={lim}_{{z}\rightarrow{x}} \left({z}−{x}\right)\varphi\left({z}\right)=\frac{{i}}{{x}}\Rightarrow \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{0} \\ $$$${if}\:\mid{x}\mid>\mathrm{1}\:\:\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\mathrm{0}\right) \\ $$$$=\mathrm{2}{i}\pi\left(\frac{−{i}}{{x}}\right)\:=\frac{\mathrm{2}\pi}{{x}}\:\:\left({we}\:{suppose}\:{x}\neq\mathrm{0}\right) \\ $$$${if}\:{x}=\mathrm{0}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{x}−{e}^{{it}} }\:=−\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{e}^{−{it}} {dt} \\ $$$$=−\left[−\frac{\mathrm{1}}{{i}}\:{e}^{−{it}} \right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:=\frac{\mathrm{1}}{{i}}\left(\mathrm{1}−\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$
