Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 51088 by ajfour last updated on 23/Dec/18

Commented by ajfour last updated on 23/Dec/18

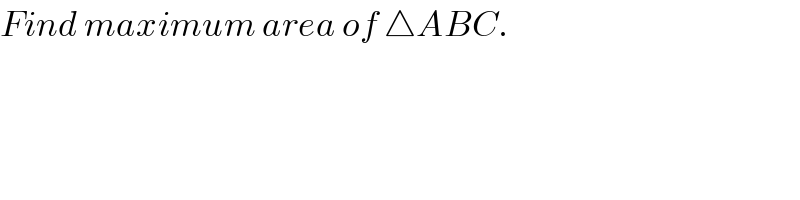
Find maximum area of △ABC.

$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{ABC}. \\ $$

Answered by ajfour last updated on 23/Dec/18

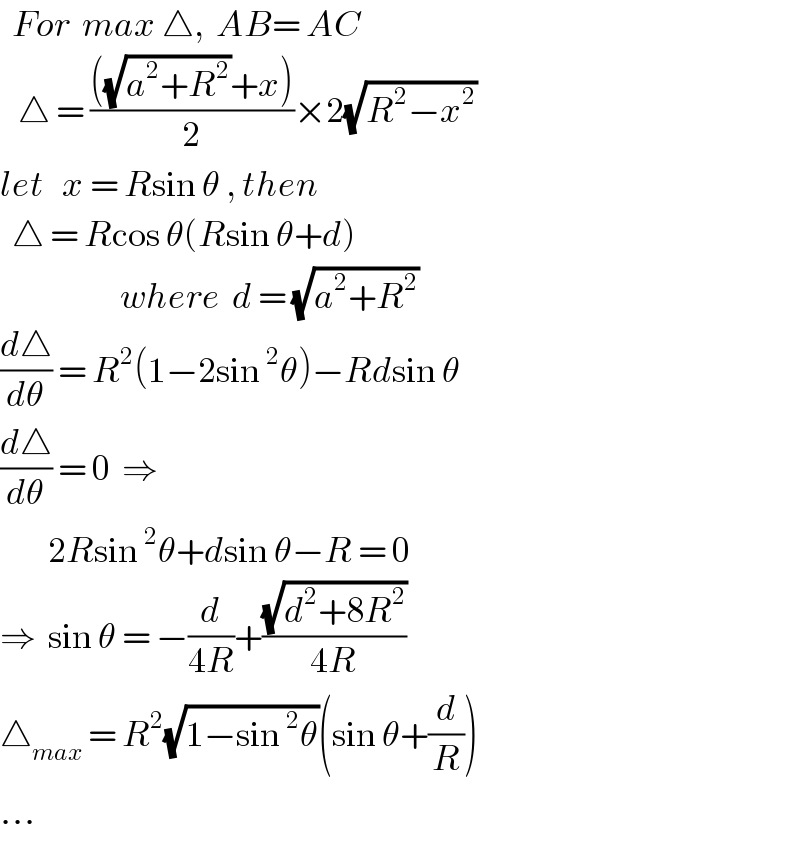
For max △, AB= AC △ = ((((√(a^2 +R^2 ))+x))/2)×2(√(R^2 −x^2 )) let x = Rsin θ , then △ = Rcos θ(Rsin θ+d) where d = (√(a^2 +R^2 )) (d△/dθ) = R^2 (1−2sin^2 θ)−Rdsin θ (d△/dθ) = 0 ⇒ 2Rsin^2 θ+dsin θ−R = 0 ⇒ sin θ = −(d/(4R))+((√(d^2 +8R^2 ))/(4R)) △_(max) = R^2 (√(1−sin^2 θ))(sin θ+(d/R)) ...

$$\:\:{For}\:\:{max}\:\bigtriangleup,\:\:{AB}=\:{AC} \\ $$$$\:\:\:\bigtriangleup\:=\:\frac{\left(\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} }+{x}\right)}{\mathrm{2}}×\mathrm{2}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${let}\:\:\:{x}\:=\:{R}\mathrm{sin}\:\theta\:,\:{then} \\ $$$$\:\:\bigtriangleup\:=\:{R}\mathrm{cos}\:\theta\left({R}\mathrm{sin}\:\theta+{d}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{where}\:\:{d}\:=\:\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} } \\ $$$$\frac{{d}\bigtriangleup}{{d}\theta}\:=\:{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \theta\right)−{Rd}\mathrm{sin}\:\theta \\ $$$$\frac{{d}\bigtriangleup}{{d}\theta}\:=\:\mathrm{0}\:\:\Rightarrow\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{R}\mathrm{sin}\:^{\mathrm{2}} \theta+{d}\mathrm{sin}\:\theta−{R}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\:=\:−\frac{{d}}{\mathrm{4}{R}}+\frac{\sqrt{{d}^{\mathrm{2}} +\mathrm{8}{R}^{\mathrm{2}} }}{\mathrm{4}{R}} \\ $$$$\bigtriangleup_{{max}} \:=\:{R}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta}\left(\mathrm{sin}\:\theta+\frac{{d}}{{R}}\right) \\ $$$$... \\ $$

Answered by mr W last updated on 24/Dec/18

O=center of circle AO=d=(√(a^2 +R^2 )) ∠BOC=2θ A=(1/2)(2Rsin θ)(d+Rcos θ)=R^2 sin θ((d/R)+cos θ) A=R^2 sin θ(λ+cos θ) with λ=(d/R)=(√(1+(a^2 /R^2 ))) (dA/dθ)=0 cos θ(λ+cos θ)−sin^2 θ=0 2cos^2 θ+λ cos θ−1=0 ⇒cos θ=(((√(λ^2 +8))−λ)/4) ⇒sin θ=((√(8−2λ^2 +2λ(√(λ^2 +8))))/4) ⇒A_(max) =((R^2 (3λ+(√(λ^2 +8)))(√(8−2λ^2 +2λ(√(λ^2 +8)))))/(16)) if point A is on the circle, ⇒d=R, λ=1 A_(max) =((R^2 (3+(√9))(√(8−2+2(√9)))))/(16))=((R^2 6(√(12)))/(16))=((3(√3)R^2 )/4) ⇒area of inscribed equilateral triangle

$${O}={center}\:{of}\:{circle} \\ $$$${AO}={d}=\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} } \\ $$$$\angle{BOC}=\mathrm{2}\theta \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{R}\mathrm{sin}\:\theta\right)\left({d}+{R}\mathrm{cos}\:\theta\right)={R}^{\mathrm{2}} \mathrm{sin}\:\theta\left(\frac{{d}}{{R}}+\mathrm{cos}\:\theta\right) \\ $$$${A}={R}^{\mathrm{2}} \mathrm{sin}\:\theta\left(\lambda+\mathrm{cos}\:\theta\right)\:{with}\:\lambda=\frac{{d}}{{R}}=\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{R}^{\mathrm{2}} }} \\ $$$$\frac{{dA}}{{d}\theta}=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta\left(\lambda+\mathrm{cos}\:\theta\right)−\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{0} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\theta+\lambda\:\mathrm{cos}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\sqrt{\lambda^{\mathrm{2}} +\mathrm{8}}−\lambda}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{8}−\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{2}\lambda\sqrt{\lambda^{\mathrm{2}} +\mathrm{8}}}}{\mathrm{4}} \\ $$$$\Rightarrow{A}_{{max}} =\frac{{R}^{\mathrm{2}} \left(\mathrm{3}\lambda+\sqrt{\lambda^{\mathrm{2}} +\mathrm{8}}\right)\sqrt{\mathrm{8}−\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{2}\lambda\sqrt{\lambda^{\mathrm{2}} +\mathrm{8}}}}{\mathrm{16}} \\ $$$$ \\ $$$${if}\:{point}\:{A}\:{is}\:{on}\:{the}\:{circle},\:\Rightarrow{d}={R},\:\lambda=\mathrm{1} \\ $$$${A}_{{max}} =\frac{\left.{R}^{\mathrm{2}} \left(\mathrm{3}+\sqrt{\mathrm{9}}\right)\sqrt{\mathrm{8}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{9}}}\right)}{\mathrm{16}}=\frac{{R}^{\mathrm{2}} \mathrm{6}\sqrt{\mathrm{12}}}{\mathrm{16}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}{R}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{area}\:{of}\:{inscribed}\:{equilateral}\:{triangle} \\ $$

Commented by ajfour last updated on 24/Dec/18

Thanks Sir!

$${Thanks}\:{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com