Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 5159 by 1771727373 last updated on 24/Apr/16

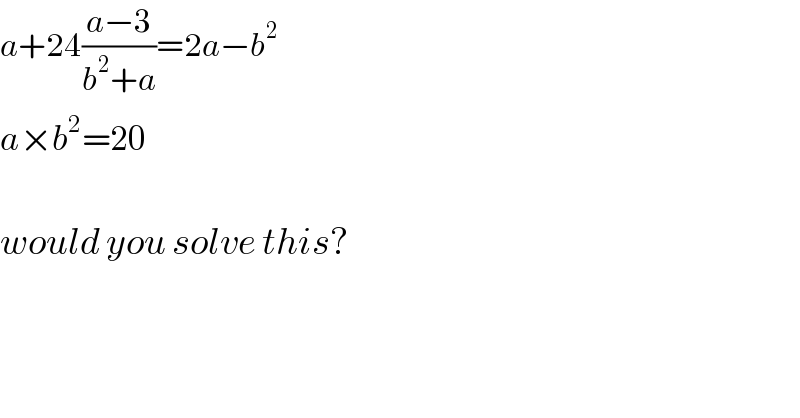
a+24((a−3)/(b^2 +a))=2a−b^(2 ) a×b^2 =20 would you solve this?

$${a}+\mathrm{24}\frac{{a}−\mathrm{3}}{{b}^{\mathrm{2}} +{a}}=\mathrm{2}{a}−{b}^{\mathrm{2}\:} \\ $$$${a}×{b}^{\mathrm{2}} =\mathrm{20} \\ $$$$ \\ $$$${would}\:{you}\:{solve}\:{this}? \\ $$

Answered by FilupSmith last updated on 24/Apr/16

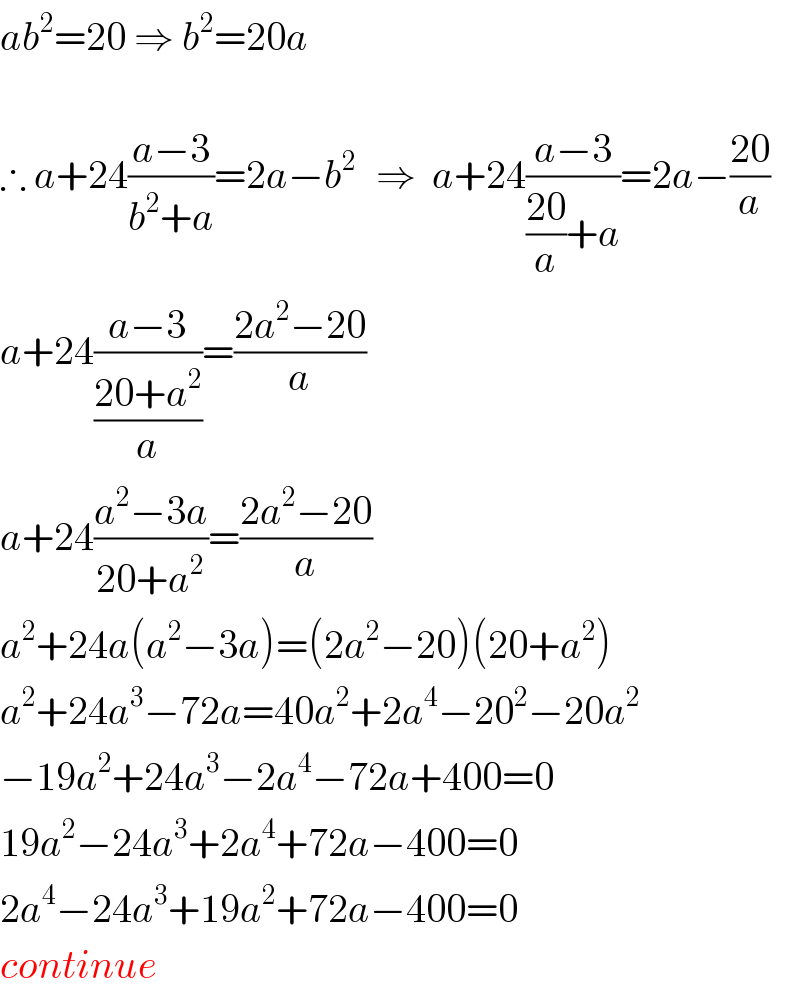
ab^2 =20 ⇒ b^2 =20a ∴ a+24((a−3)/(b^2 +a))=2a−b^(2 ) ⇒ a+24((a−3)/(((20)/a)+a))=2a−((20)/a) a+24((a−3)/((20+a^2 )/a))=((2a^2 −20)/a) a+24((a^2 −3a)/(20+a^2 ))=((2a^2 −20)/a) a^2 +24a(a^2 −3a)=(2a^2 −20)(20+a^2 ) a^2 +24a^3 −72a=40a^2 +2a^4 −20^2 −20a^2 −19a^2 +24a^3 −2a^4 −72a+400=0 19a^2 −24a^3 +2a^4 +72a−400=0 2a^4 −24a^3 +19a^2 +72a−400=0 continue

$${ab}^{\mathrm{2}} =\mathrm{20}\:\Rightarrow\:{b}^{\mathrm{2}} =\mathrm{20}{a} \\ $$$$ \\ $$$$\therefore\:{a}+\mathrm{24}\frac{{a}−\mathrm{3}}{{b}^{\mathrm{2}} +{a}}=\mathrm{2}{a}−{b}^{\mathrm{2}\:} \:\:\Rightarrow\:\:{a}+\mathrm{24}\frac{{a}−\mathrm{3}}{\frac{\mathrm{20}}{{a}}+{a}}=\mathrm{2}{a}−\frac{\mathrm{20}}{{a}} \\ $$$${a}+\mathrm{24}\frac{{a}−\mathrm{3}}{\frac{\mathrm{20}+{a}^{\mathrm{2}} }{{a}}}=\frac{\mathrm{2}{a}^{\mathrm{2}} −\mathrm{20}}{{a}} \\ $$$${a}+\mathrm{24}\frac{{a}^{\mathrm{2}} −\mathrm{3}{a}}{\mathrm{20}+{a}^{\mathrm{2}} }=\frac{\mathrm{2}{a}^{\mathrm{2}} −\mathrm{20}}{{a}} \\ $$$${a}^{\mathrm{2}} +\mathrm{24}{a}\left({a}^{\mathrm{2}} −\mathrm{3}{a}\right)=\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{20}\right)\left(\mathrm{20}+{a}^{\mathrm{2}} \right) \\ $$$${a}^{\mathrm{2}} +\mathrm{24}{a}^{\mathrm{3}} −\mathrm{72}{a}=\mathrm{40}{a}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{4}} −\mathrm{20}^{\mathrm{2}} −\mathrm{20}{a}^{\mathrm{2}} \\ $$$$−\mathrm{19}{a}^{\mathrm{2}} +\mathrm{24}{a}^{\mathrm{3}} −\mathrm{2}{a}^{\mathrm{4}} −\mathrm{72}{a}+\mathrm{400}=\mathrm{0} \\ $$$$\mathrm{19}{a}^{\mathrm{2}} −\mathrm{24}{a}^{\mathrm{3}} +\mathrm{2}{a}^{\mathrm{4}} +\mathrm{72}{a}−\mathrm{400}=\mathrm{0} \\ $$$$\mathrm{2}{a}^{\mathrm{4}} −\mathrm{24}{a}^{\mathrm{3}} +\mathrm{19}{a}^{\mathrm{2}} +\mathrm{72}{a}−\mathrm{400}=\mathrm{0} \\ $$$${continue} \\ $$

Answered by Yozzii last updated on 28/Apr/16

a(b^2 +a)+24(a−3)=(2a−b^2 )(b^2 +a) ab^2 +a^2 +24a−72=2ab^2 +2a^2 −b^4 −ab^2 b^4 −a^2 +24a−72=0 b^4 =a^2 −24a+72 b^4 =((400)/a^2 ) ∴ 400=a^4 −24a^3 +72a^2 a^4 −24a^3 +72a^2 −400=0 (∗) Let f(x)=x^4 −24x^3 +72x^2 −400. By trial and error, and application of the intermediate value theorem, a root for the equation exists in the interval [20.5,20.6]. f^′ (x)=4x^3 −72x^2 +144x By the Newton−Raphson method the n+1 th approximation to the root of f(x)=0, given the n th approximation, is found by x_(n+1) =x_n −((f(x_n ))/(f^′ (x_n ))) x_(n+1) =((3x_n ^4 −48x_n ^3 +72x_n ^2 +400)/(4x_n ^3 −72x_n ^2 +144x_n )) Let x_1 =((20.5+20.6)/2)=20.55. ⇒x_2 ≈20.540974 ⇒x_3 ≈20.540961 ⇒x_4 ≈20.540961 ∴ a≈20.541. Note that (∗) has more than just one real root. This same method could be used to search for other real roots. Since b^2 =((20)/a), if b∈R⇒a>0 ∴ b=±(√((20)/(20.541)))≈±0.9867

$${a}\left({b}^{\mathrm{2}} +{a}\right)+\mathrm{24}\left({a}−\mathrm{3}\right)=\left(\mathrm{2}{a}−{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +{a}\right) \\ $$$${ab}^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{24}{a}−\mathrm{72}=\mathrm{2}{ab}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} −{b}^{\mathrm{4}} −{ab}^{\mathrm{2}} \\ $$$${b}^{\mathrm{4}} −{a}^{\mathrm{2}} +\mathrm{24}{a}−\mathrm{72}=\mathrm{0} \\ $$$${b}^{\mathrm{4}} ={a}^{\mathrm{2}} −\mathrm{24}{a}+\mathrm{72} \\ $$$${b}^{\mathrm{4}} =\frac{\mathrm{400}}{{a}^{\mathrm{2}} } \\ $$$$\therefore\:\mathrm{400}={a}^{\mathrm{4}} −\mathrm{24}{a}^{\mathrm{3}} +\mathrm{72}{a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{4}} −\mathrm{24}{a}^{\mathrm{3}} +\mathrm{72}{a}^{\mathrm{2}} −\mathrm{400}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\left(\ast\right) \\ $$$$ \\ $$$${Let}\:{f}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{24}{x}^{\mathrm{3}} +\mathrm{72}{x}^{\mathrm{2}} −\mathrm{400}. \\ $$$${By}\:{trial}\:{and}\:{error},\:{and}\:{application} \\ $$$${of}\:{the}\:{intermediate}\:{value}\:{theorem},\: \\ $$$${a}\:{root}\:{for}\:{the}\:{equation}\:{exists}\:{in} \\ $$$${the}\:{interval}\:\left[\mathrm{20}.\mathrm{5},\mathrm{20}.\mathrm{6}\right]. \\ $$$${f}^{'} \left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} −\mathrm{72}{x}^{\mathrm{2}} +\mathrm{144}{x} \\ $$$${By}\:{the}\:{Newton}−{Raphson}\:{method} \\ $$$${the}\:{n}+\mathrm{1}\:{th}\:{approximation}\:{to}\:{the} \\ $$$${root}\:{of}\:{f}\left({x}\right)=\mathrm{0},\:{given}\:{the}\:{n}\:{th}\:{approximation}, \\ $$$${is}\:{found}\:{by} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{{f}\left({x}_{{n}} \right)}{{f}^{'} \left({x}_{{n}} \right)} \\ $$$${x}_{{n}+\mathrm{1}} =\frac{\mathrm{3}{x}_{{n}} ^{\mathrm{4}} −\mathrm{48}{x}_{{n}} ^{\mathrm{3}} +\mathrm{72}{x}_{{n}} ^{\mathrm{2}} +\mathrm{400}}{\mathrm{4}{x}_{{n}} ^{\mathrm{3}} −\mathrm{72}{x}_{{n}} ^{\mathrm{2}} +\mathrm{144}{x}_{{n}} } \\ $$$${Let}\:{x}_{\mathrm{1}} =\frac{\mathrm{20}.\mathrm{5}+\mathrm{20}.\mathrm{6}}{\mathrm{2}}=\mathrm{20}.\mathrm{55}. \\ $$$$\Rightarrow{x}_{\mathrm{2}} \approx\mathrm{20}.\mathrm{540974} \\ $$$$\Rightarrow{x}_{\mathrm{3}} \approx\mathrm{20}.\mathrm{540961} \\ $$$$\Rightarrow{x}_{\mathrm{4}} \approx\mathrm{20}.\mathrm{540961} \\ $$$$\therefore\:{a}\approx\mathrm{20}.\mathrm{541}.\:{Note}\:{that}\:\left(\ast\right)\:{has}\:{more} \\ $$$${than}\:{just}\:{one}\:{real}\:{root}.\:{This}\:{same} \\ $$$${method}\:{could}\:{be}\:{used}\:{to}\:{search}\:{for} \\ $$$${other}\:{real}\:{roots}.\:{Since}\:{b}^{\mathrm{2}} =\frac{\mathrm{20}}{{a}},\:{if} \\ $$$${b}\in\mathbb{R}\Rightarrow{a}>\mathrm{0}\:\therefore\:{b}=\pm\sqrt{\frac{\mathrm{20}}{\mathrm{20}.\mathrm{541}}}\approx\pm\mathrm{0}.\mathrm{9867} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com