
Question Number 52099 by ajfour last updated on 03/Jan/19

Commented by ajfour last updated on 03/Jan/19

$${Find}\:\theta\left({t}\right). \\ $$
Answered by mr W last updated on 03/Jan/19
![l=length of right string l=(√(a^2 +(a+b)^2 −2a(a+b) cos θ)) (dl/dθ)=((a(a+b) sin θ)/(√(a^2 +(a+b)^2 −2a(a+b) cos θ))) ω=(dθ/dt) (dl/dt)=(dl/dθ)×(dθ/dt)=((a(a+b) sin θ)/(√(a^2 +(a+b)^2 −2a(a+b) cos θ))) ω ω_M =(dl/(Rdt))=((a(a+b) sin θ)/(R(√(a^2 +(a+b)^2 −2a(a+b) cos θ)))) ω mgasin θ=(1/2)m(aω)^2 +(1/2)Iω_M ^2 mgasin θ=(1/2)ma^2 ω^2 +(1/2)×((MR^2 )/2)×((a^2 (a+b)^2 sin^2 θ ω^2 )/(R^2 [a^2 +(a+b)^2 −2a(a+b) cos θ])) 2gsin θ=aω^2 {1+((M(a+b)^2 sin^2 θ)/(2m[a^2 +(a+b)^2 −2a(a+b) cos θ]))} ((2g)/a)=ω^2 {(1/(sin θ))+(((a+b)M)/(4am))×((sin θ)/(((a^2 +(a+b)^2 )/(2a(a+b)))−cos θ))} with λ=((a^2 +(a+b)^2 )/(2a(a+b))), μ=(((a+b)M)/(4am)) ((2g)/a)=ω^2 {(1/(sin θ))+((μ sin θ)/(λ−cos θ))} (√((2g)/a))=ω(√((1/(sin θ))+((μ sin θ)/(λ−cos θ)))) ω=(dθ/dt) ⇒∫_0 ^θ (√((1/(sin θ))+((μ sin θ)/(λ−cos θ)))) dθ=∫_0 ^t (√((2g)/a)) dt ⇒∫_0 ^θ (√((1/(sin θ))+((μ sin θ)/(λ−cos θ)))) dθ=(√((2g)/a)) t ..... i can not solve this integral .....](Q52110.png)
$${l}={length}\:{of}\:{right}\:{string} \\ $$$${l}=\sqrt{{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\:\mathrm{cos}\:\theta} \\ $$$$\frac{{dl}}{{d}\theta}=\frac{{a}\left({a}+{b}\right)\:\mathrm{sin}\:\theta}{\sqrt{{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\:\mathrm{cos}\:\theta}} \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$$\frac{{dl}}{{dt}}=\frac{{dl}}{{d}\theta}×\frac{{d}\theta}{{dt}}=\frac{{a}\left({a}+{b}\right)\:\mathrm{sin}\:\theta}{\sqrt{{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\:\mathrm{cos}\:\theta}}\:\omega \\ $$$$\omega_{{M}} =\frac{{dl}}{{Rdt}}=\frac{{a}\left({a}+{b}\right)\:\mathrm{sin}\:\theta}{{R}\sqrt{{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\:\mathrm{cos}\:\theta}}\:\omega \\ $$$${mga}\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}{m}\left({a}\omega\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{I}\omega_{{M}} ^{\mathrm{2}} \\ $$$${mga}\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}{ma}^{\mathrm{2}} \omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{{MR}^{\mathrm{2}} }{\mathrm{2}}×\frac{{a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\:\omega^{\mathrm{2}} }{{R}^{\mathrm{2}} \left[{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\:\mathrm{cos}\:\theta\right]} \\ $$$$\mathrm{2}{g}\mathrm{sin}\:\theta={a}\omega^{\mathrm{2}} \left\{\mathrm{1}+\frac{{M}\left({a}+{b}\right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}{m}\left[{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\:\mathrm{cos}\:\theta\right]}\right\} \\ $$$$\frac{\mathrm{2}{g}}{{a}}=\omega^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+\frac{\left({a}+{b}\right){M}}{\mathrm{4}{am}}×\frac{\mathrm{sin}\:\theta}{\frac{{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}{a}\left({a}+{b}\right)}−\mathrm{cos}\:\theta}\right\} \\ $$$${with}\:\lambda=\frac{{a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}{a}\left({a}+{b}\right)},\:\mu=\frac{\left({a}+{b}\right){M}}{\mathrm{4}{am}} \\ $$$$\frac{\mathrm{2}{g}}{{a}}=\omega^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+\frac{\mu\:\mathrm{sin}\:\theta}{\lambda−\mathrm{cos}\:\theta}\right\} \\ $$$$\sqrt{\frac{\mathrm{2}{g}}{{a}}}=\omega\sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+\frac{\mu\:\mathrm{sin}\:\theta}{\lambda−\mathrm{cos}\:\theta}} \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\theta} \sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+\frac{\mu\:\mathrm{sin}\:\theta}{\lambda−\mathrm{cos}\:\theta}}\:{d}\theta=\int_{\mathrm{0}} ^{{t}} \sqrt{\frac{\mathrm{2}{g}}{{a}}}\:{dt} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\theta} \sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+\frac{\mu\:\mathrm{sin}\:\theta}{\lambda−\mathrm{cos}\:\theta}}\:{d}\theta=\sqrt{\frac{\mathrm{2}{g}}{{a}}}\:{t} \\ $$$$.....\:{i}\:{can}\:{not}\:{solve}\:{this}\:{integral}\:..... \\ $$
Commented by ajfour last updated on 03/Jan/19
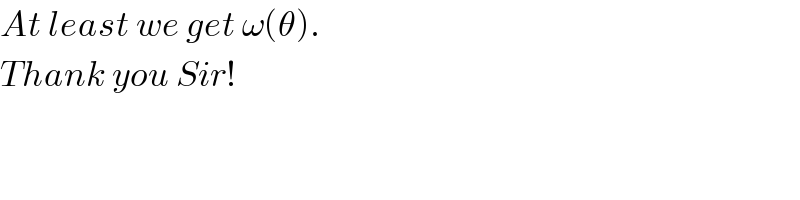
$${At}\:{least}\:{we}\:{get}\:\omega\left(\theta\right).\: \\ $$$${Thank}\:{you}\:{Sir}! \\ $$
