Question Number 52140 by ajfour last updated on 03/Jan/19
Commented by ajfour last updated on 03/Jan/19

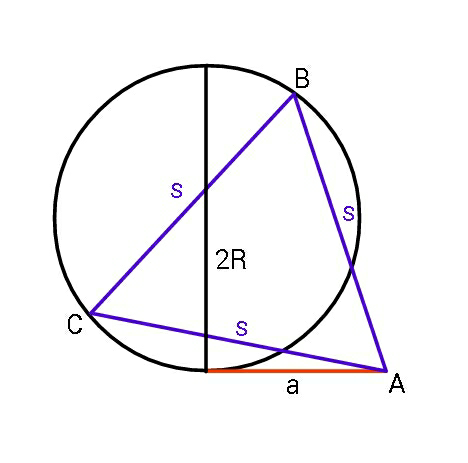
$${Find}\:{side}\:\boldsymbol{{s}}\:{of}\:{the}\:{equilateral} \\ $$$${triangles}\:{possible}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}\:\&\:\boldsymbol{{R}}. \\ $$$${For}\:{what}\:{maximum}\:{value}\:{of}\:\boldsymbol{{a}}_{\mathrm{0}} \\ $$$${is}\:{such}\:\:{triangle}\:{possible}.\:{What}\:{is} \\ $$$${the}\:{side}\:\boldsymbol{{s}}\:{for}\:{this}\:{value}\:{of}\:\boldsymbol{{a}}_{\mathrm{0}} \:. \\ $$
Commented by Olalekan99 last updated on 04/Jan/19

$${pls}\:{which}\:{did}\:{u}\:{use}\:{for}\:{sketching} \\ $$$${or}\:{is}\:{it}\:{dis}\:{same}\:{app} \\ $$
Answered by mr W last updated on 03/Jan/19
Commented by mr W last updated on 03/Jan/19
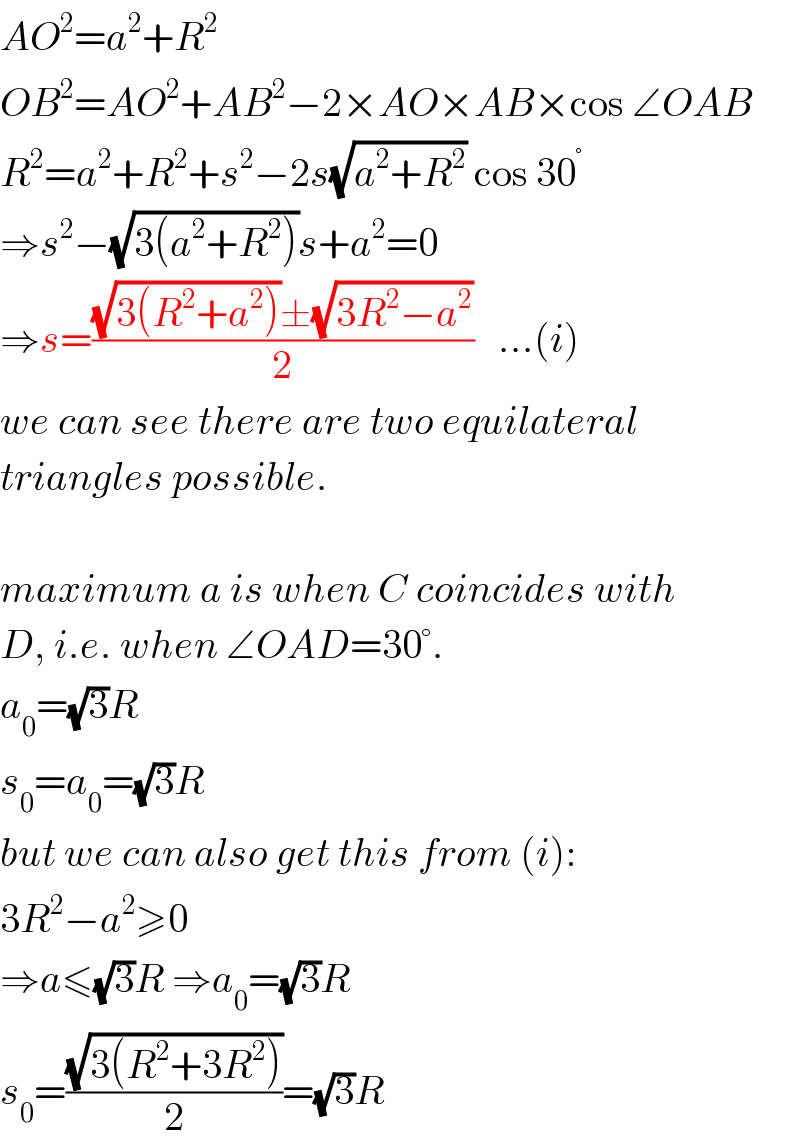
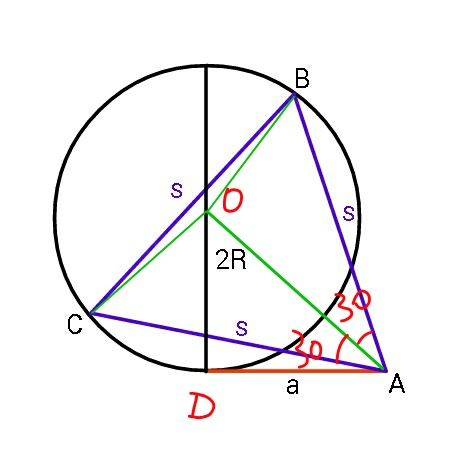
$${AO}^{\mathrm{2}} ={a}^{\mathrm{2}} +{R}^{\mathrm{2}} \\ $$$${OB}^{\mathrm{2}} ={AO}^{\mathrm{2}} +{AB}^{\mathrm{2}} −\mathrm{2}×{AO}×{AB}×\mathrm{cos}\:\angle{OAB} \\ $$$${R}^{\mathrm{2}} ={a}^{\mathrm{2}} +{R}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}{s}\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} }\:\mathrm{cos}\:\mathrm{30}^{°} \\ $$$$\Rightarrow{s}^{\mathrm{2}} −\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} +{R}^{\mathrm{2}} \right)}{s}+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}=\frac{\sqrt{\mathrm{3}\left({R}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}\pm\sqrt{\mathrm{3}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}}\:\:\:...\left({i}\right) \\ $$$${we}\:{can}\:{see}\:{there}\:{are}\:{two}\:{equilateral} \\ $$$${triangles}\:{possible}. \\ $$$$ \\ $$$${maximum}\:{a}\:{is}\:{when}\:{C}\:{coincides}\:{with} \\ $$$${D},\:{i}.{e}.\:{when}\:\angle{OAD}=\mathrm{30}°. \\ $$$${a}_{\mathrm{0}} =\sqrt{\mathrm{3}}{R} \\ $$$${s}_{\mathrm{0}} ={a}_{\mathrm{0}} =\sqrt{\mathrm{3}}{R} \\ $$$${but}\:{we}\:{can}\:{also}\:{get}\:{this}\:{from}\:\left({i}\right): \\ $$$$\mathrm{3}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow{a}\leqslant\sqrt{\mathrm{3}}{R}\:\Rightarrow{a}_{\mathrm{0}} =\sqrt{\mathrm{3}}{R} \\ $$$${s}_{\mathrm{0}} =\frac{\sqrt{\mathrm{3}\left({R}^{\mathrm{2}} +\mathrm{3}{R}^{\mathrm{2}} \right)}}{\mathrm{2}}=\sqrt{\mathrm{3}}{R} \\ $$
Commented by ajfour last updated on 03/Jan/19
$${Correct}\:{and}\:{intelligent}\:{way}\:{Sir}. \\ $$$${Thanks}\:{again}!\:{But}\:{what}\:{if}\:{we}\:{have} \\ $$$${parabola}\:\:{y}={x}^{\mathrm{2}} \:{instead}\:{of}\:{the}\:{circle}, \\ $$$${with}\:{D}\:{as}\:{origin}\:? \\ $$
Answered by mr W last updated on 04/Jan/19
![solution for parabola instead of circle: eqn. of parabola: y=cx^2 with c=1 A(a, 0), a≥0 B(p, cp^2 ) C(q, cq^2 ) AB^2 =s^2 =(p−a)^2 +c^2 p^4 AC^2 =s^2 =(q−a)^2 +c^2 q^4 BC^2 =s^2 =(p−q)^2 +c^2 (p^2 −q^2 )^2 (p−a)^2 +c^2 p^4 =(q−a)^2 +c^2 q^4 p^2 −2ap+c^2 p^4 =q^2 −2aq+c^2 q^4 ⇒(p+q)[1+c^2 (p^2 +q^2 )]=2a (p−a)^2 +c^2 p^4 =(p−q)^2 +c^2 (p^2 −q^2 )^2 p^2 −2ap+a^2 +c^2 p^4 =p^2 +q^2 −2pq+c^2 p^4 −2c^2 p^2 q^2 +c^2 q^4 ⇒a^2 −2ap=q^2 −2pq−2c^2 p^2 q^2 +c^2 q^4 for c=1: ⇒(p+q)(1+p^2 +q^2 )=2a ...(i) ⇒a^2 −2ap=q^2 −2pq−2p^2 q^2 +q^4 ...(ii) from (ii): 2q^2 p^2 −2(a−q)p+a^2 −q^2 −q^4 =0 ⇒p=((a−q±(√((a−q)^2 −2q^2 (a^2 −q^2 −q^4 ))))/(2q^2 )) putting this into (i) we get an eqn. for q. for a given a there can be − no solution − one or more solutions examples: a=2: q=1.9741⇒p=−1.3878⇒s=3.8971 q=1.2310⇒p=0.3031⇒s=1.6992 q=0.3031⇒p=1.2310 (as above) q=−1.3878⇒p=1.9741 (as above) a_(max) =4.13765: q=2.0284⇒p=−0.4803⇒s=4.6235 q=−0.4803⇒p=2.0284 (as above)](Q52171.png)
$${solution}\:{for}\:{parabola}\:{instead}\:{of}\:{circle}: \\ $$$${eqn}.\:{of}\:{parabola}: \\ $$$${y}={cx}^{\mathrm{2}} \:{with}\:{c}=\mathrm{1} \\ $$$${A}\left({a},\:\mathrm{0}\right),\:{a}\geqslant\mathrm{0} \\ $$$${B}\left({p},\:{cp}^{\mathrm{2}} \right) \\ $$$${C}\left({q},\:{cq}^{\mathrm{2}} \right) \\ $$$${AB}^{\mathrm{2}} ={s}^{\mathrm{2}} =\left({p}−{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {p}^{\mathrm{4}} \\ $$$${AC}^{\mathrm{2}} ={s}^{\mathrm{2}} =\left({q}−{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {q}^{\mathrm{4}} \\ $$$${BC}^{\mathrm{2}} ={s}^{\mathrm{2}} =\left({p}−{q}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\left({p}−{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {p}^{\mathrm{4}} =\left({q}−{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {q}^{\mathrm{4}} \\ $$$${p}^{\mathrm{2}} −\mathrm{2}{ap}+{c}^{\mathrm{2}} {p}^{\mathrm{4}} ={q}^{\mathrm{2}} −\mathrm{2}{aq}+{c}^{\mathrm{2}} {q}^{\mathrm{4}} \\ $$$$\Rightarrow\left({p}+{q}\right)\left[\mathrm{1}+{c}^{\mathrm{2}} \left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\right]=\mathrm{2}{a} \\ $$$$ \\ $$$$\left({p}−{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} {p}^{\mathrm{4}} =\left({p}−{q}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} −\mathrm{2}{ap}+{a}^{\mathrm{2}} +{c}^{\mathrm{2}} {p}^{\mathrm{4}} ={p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}+{c}^{\mathrm{2}} {p}^{\mathrm{4}} −\mathrm{2}{c}^{\mathrm{2}} {p}^{\mathrm{2}} {q}^{\mathrm{2}} +{c}^{\mathrm{2}} {q}^{\mathrm{4}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −\mathrm{2}{ap}={q}^{\mathrm{2}} −\mathrm{2}{pq}−\mathrm{2}{c}^{\mathrm{2}} {p}^{\mathrm{2}} {q}^{\mathrm{2}} +{c}^{\mathrm{2}} {q}^{\mathrm{4}} \\ $$$${for}\:{c}=\mathrm{1}: \\ $$$$\Rightarrow\left({p}+{q}\right)\left(\mathrm{1}+{p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\mathrm{2}{a}\:\:\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} −\mathrm{2}{ap}={q}^{\mathrm{2}} −\mathrm{2}{pq}−\mathrm{2}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{4}} \:\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({ii}\right): \\ $$$$\mathrm{2}{q}^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{2}\left({a}−{q}\right){p}+{a}^{\mathrm{2}} −{q}^{\mathrm{2}} −{q}^{\mathrm{4}} =\mathrm{0}\:\: \\ $$$$\Rightarrow{p}=\frac{{a}−{q}\pm\sqrt{\left({a}−{q}\right)^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{q}^{\mathrm{2}} −{q}^{\mathrm{4}} \right)}}{\mathrm{2}{q}^{\mathrm{2}} } \\ $$$${putting}\:{this}\:{into}\:\left({i}\right)\:{we}\:{get}\:{an}\:{eqn}.\:{for}\:{q}. \\ $$$$ \\ $$$${for}\:{a}\:{given}\:\boldsymbol{{a}}\:{there}\:{can}\:{be}\: \\ $$$$−\:{no}\:{solution} \\ $$$$−\:{one}\:{or}\:{more}\:{solutions} \\ $$$$ \\ $$$${examples}: \\ $$$${a}=\mathrm{2}: \\ $$$${q}=\mathrm{1}.\mathrm{9741}\Rightarrow{p}=−\mathrm{1}.\mathrm{3878}\Rightarrow{s}=\mathrm{3}.\mathrm{8971} \\ $$$${q}=\mathrm{1}.\mathrm{2310}\Rightarrow{p}=\mathrm{0}.\mathrm{3031}\Rightarrow{s}=\mathrm{1}.\mathrm{6992} \\ $$$${q}=\mathrm{0}.\mathrm{3031}\Rightarrow{p}=\mathrm{1}.\mathrm{2310}\:\left({as}\:{above}\right) \\ $$$${q}=−\mathrm{1}.\mathrm{3878}\Rightarrow{p}=\mathrm{1}.\mathrm{9741}\:\left({as}\:{above}\right) \\ $$$$ \\ $$$${a}_{{max}} =\mathrm{4}.\mathrm{13765}: \\ $$$${q}=\mathrm{2}.\mathrm{0284}\Rightarrow{p}=−\mathrm{0}.\mathrm{4803}\Rightarrow{s}=\mathrm{4}.\mathrm{6235} \\ $$$${q}=−\mathrm{0}.\mathrm{4803}\Rightarrow{p}=\mathrm{2}.\mathrm{0284}\:\left({as}\:{above}\right) \\ $$
Commented by ajfour last updated on 04/Jan/19

$${Thanks}\:{for}\:{it},\:{Sir}. \\ $$
Commented by mr W last updated on 04/Jan/19
Commented by mr W last updated on 04/Jan/19
Commented by mr W last updated on 04/Jan/19
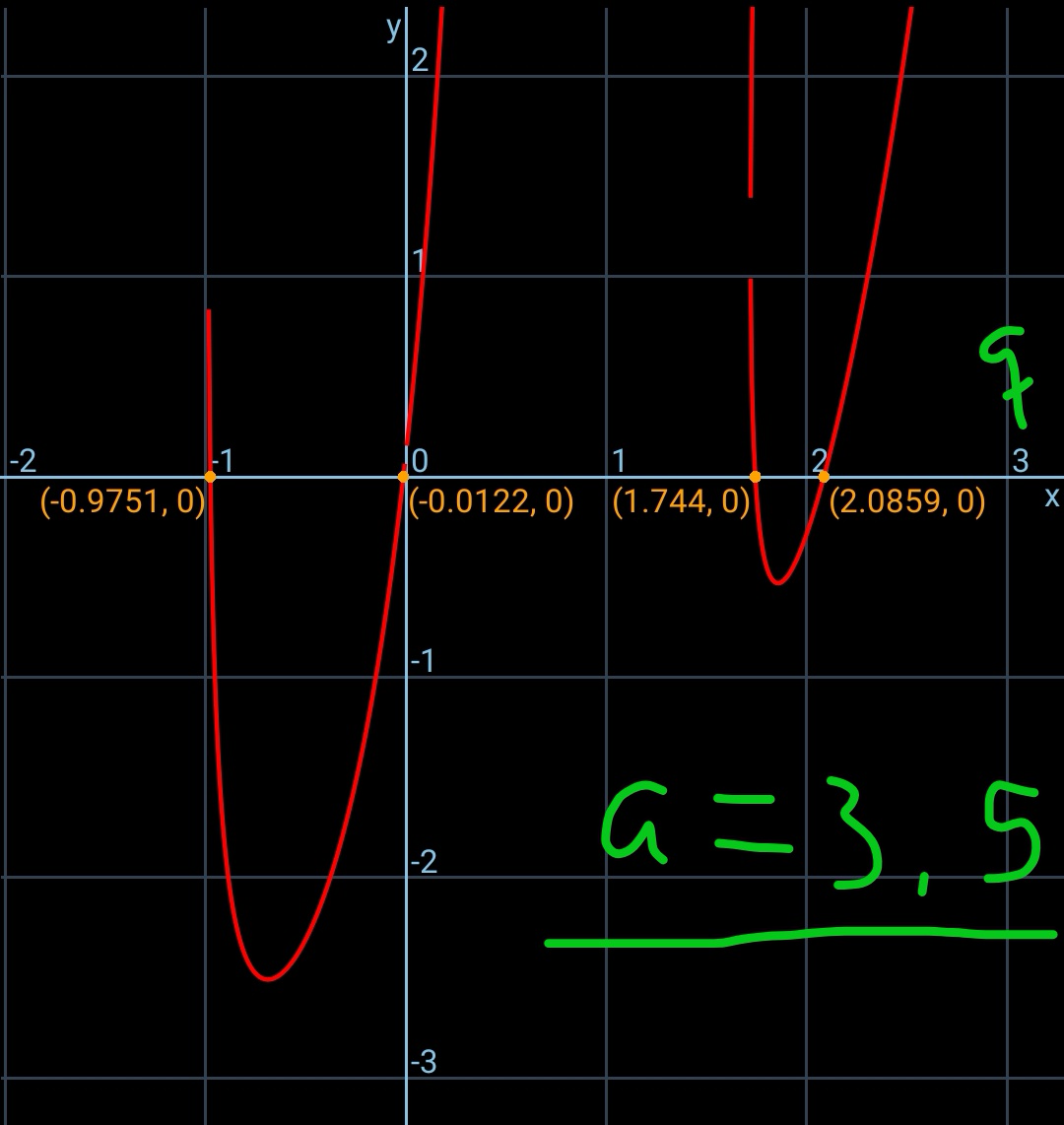
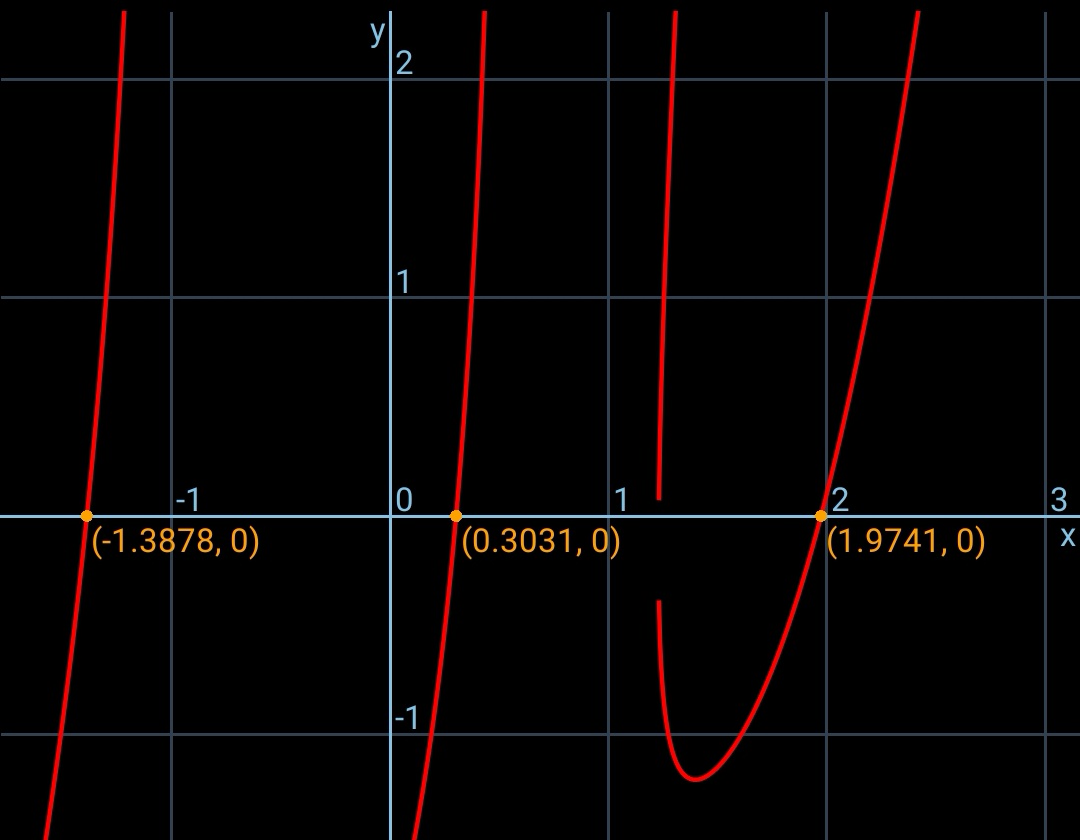
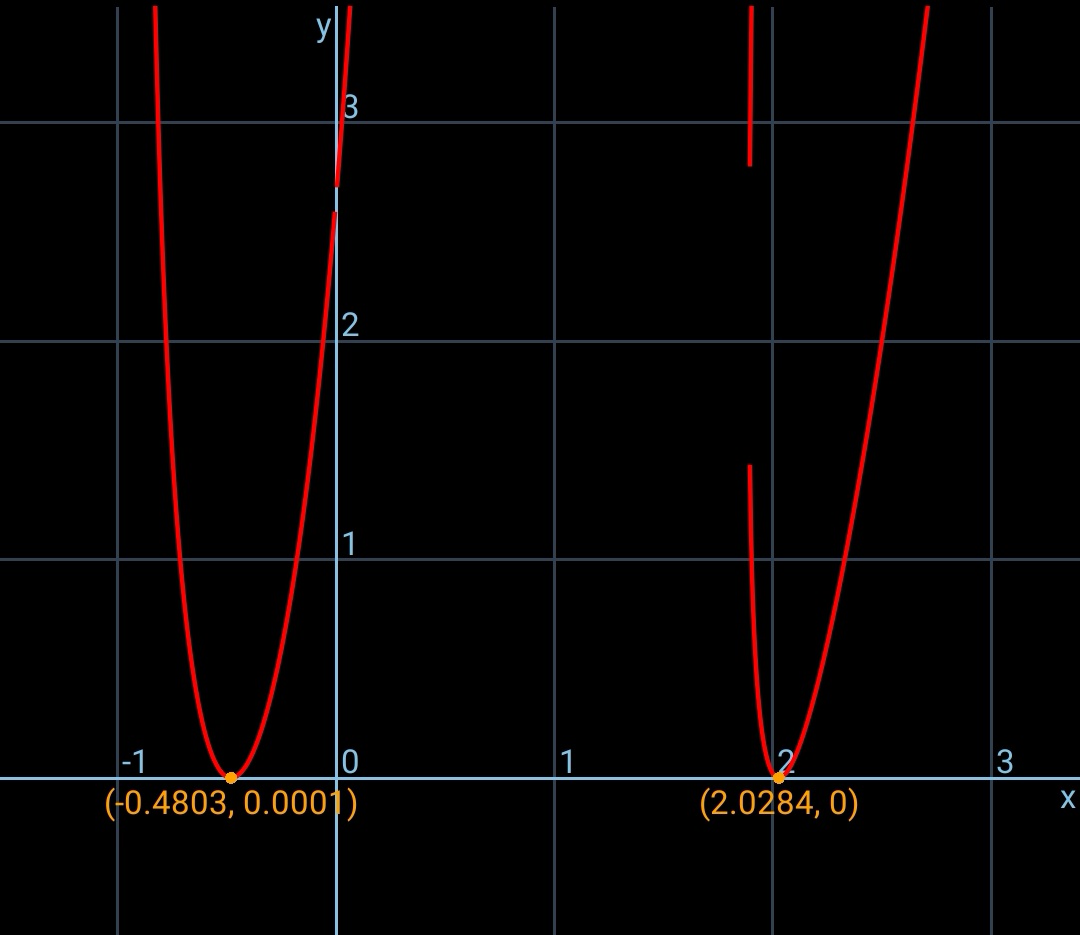
$${i}\:{have}\:{reduced}\:{to}\:{a}\:{single}\:{eqn}.\:{which} \\ $$$${can}\:{be}\:{solved}\:{nummerically}. \\ $$
Commented by mr W last updated on 04/Jan/19
![from eqn. (ii) we get p in terms of q: p=((a−q±(√((a−q)^2 −2q^2 (a^2 −q^2 −q^4 ))))/(2q^2 ))=p(q) the eqn. (i) is then an eqn. of q alone: [p(q)+q][1+p^2 (q)+q^2 ]−2a=0 from which we can solve for q by graph method as shown in the diagram. usually there are 4 roots for q. due to symmetry these 4 roots represent in reality 2 different equilateral triangles.](Q52216.png)
$${from}\:{eqn}.\:\left({ii}\right)\:{we}\:{get}\:{p}\:{in}\:{terms}\:{of}\:{q}: \\ $$$${p}=\frac{{a}−{q}\pm\sqrt{\left({a}−{q}\right)^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{q}^{\mathrm{2}} −{q}^{\mathrm{4}} \right)}}{\mathrm{2}{q}^{\mathrm{2}} }={p}\left({q}\right) \\ $$$${the}\:{eqn}.\:\left({i}\right)\:{is}\:{then}\:{an}\:{eqn}.\:{of}\:{q}\:{alone}: \\ $$$$\left[{p}\left({q}\right)+{q}\right]\left[\mathrm{1}+{p}^{\mathrm{2}} \left({q}\right)+{q}^{\mathrm{2}} \right]−\mathrm{2}{a}=\mathrm{0} \\ $$$${from}\:{which}\:{we}\:{can}\:{solve}\:{for}\:{q}\:{by} \\ $$$${graph}\:{method}\:{as}\:{shown}\:{in}\:{the} \\ $$$${diagram}.\:{usually}\:{there}\:{are}\:\mathrm{4}\:{roots} \\ $$$${for}\:{q}.\:{due}\:{to}\:{symmetry}\:{these}\:\mathrm{4}\:{roots} \\ $$$${represent}\:{in}\:{reality}\:\mathrm{2}\:{different}\:{equilateral} \\ $$$${triangles}. \\ $$
Commented by ajfour last updated on 04/Jan/19

$${but}\:{there}\:{we}\:{have}\:{both}\:{p}\:{and}\:{q}, \\ $$$${and}\:{p}\:{isn}'{t}\:{easy}\:{in}\:{terms}\:{of}\:{q}\:{from} \\ $$$${the}\:{other}\:{equation},\:{Sir}. \\ $$$${Thanks}\:{for}\:{as}\:{much}\:{you}\:{brought}\:{out}! \\ $$
Commented by mr W last updated on 04/Jan/19