
Question Number 53293 by gunawan last updated on 20/Jan/19
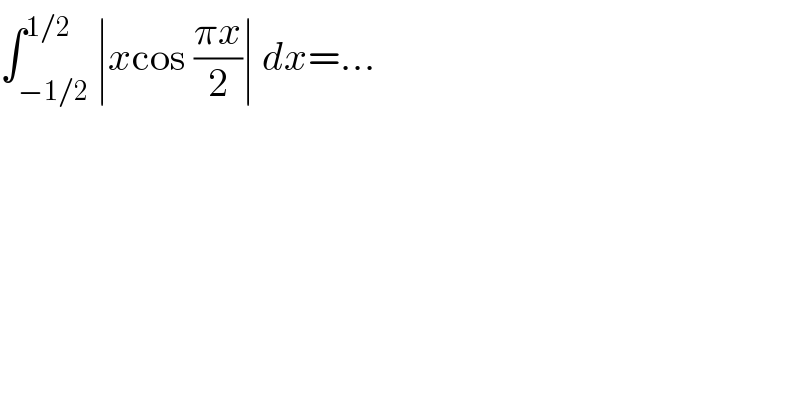
$$\int_{−\mathrm{1}/\mathrm{2}} ^{\mathrm{1}/\mathrm{2}} \mid{x}\mathrm{cos}\:\frac{\pi{x}}{\mathrm{2}}\mid\:{dx}=... \\ $$
Commented by maxmathsup by imad last updated on 20/Jan/19
![we have f(x)=∣xcos(((πx)/2))∣=∣x∣∣cos(((πx)/2))∣ is a even function so I=∫_(−(1/2)) ^(1/2) f(x)dx =2 ∫_0 ^(1/2) x∣cos(((πx)/2))∣ dx but 0≤x≤(1/2) ⇒0≤πx≤(π/2) ⇒0≤((πx)/2)≤(π/4) ⇒ cos(((πx)/2))≥0 ⇒ I =2 ∫_0 ^(1/2) x cos(((πx)/2))dx by parts u=x and v^′ =cos(((πx)/2)) ⇒ I =2{ [(2/π)sin(((πx)/2))x]_0 ^(1/2) −∫_0 ^(1/2) (2/π)sin(((πx)/2))dx} =2{(1/π)((√2)/2)}−(4/π)∫_0 ^(1/2) sin(((πx)/2))dx =((√2)/π) +(4/π) [(2/π)cos(((πx)/2))]_0 ^(1/2) =((√2)/π) +(8/π^2 )( ((√2)/2) −1) =((√2)/π) +(1/π^2 )(4(√2)−8) =((π(√2)+4(√2)−8)/π^2 ) .](Q53308.png)
$${we}\:{have}\:{f}\left({x}\right)=\mid{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid=\mid{x}\mid\mid{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid\:{is}\:{a}\:{even}\:{function}\:{so} \\ $$$${I}=\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {f}\left({x}\right){dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {x}\mid{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid\:{dx}\:\:{but}\:\:\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{0}\leqslant\pi{x}\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{0}\leqslant\frac{\pi{x}}{\mathrm{2}}\leqslant\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\:{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\geqslant\mathrm{0}\:\Rightarrow\:{I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:{x}\:{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right){dx}\:{by}\:{parts}\:{u}={x}\:{and}\:{v}^{'} ={cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\left\{\:\:\left[\frac{\mathrm{2}}{\pi}{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right){x}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{2}}{\pi}{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right){dx}\right\} \\ $$$$=\mathrm{2}\left\{\frac{\mathrm{1}}{\pi}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right\}−\frac{\mathrm{4}}{\pi}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right){dx}\:=\frac{\sqrt{\mathrm{2}}}{\pi}\:+\frac{\mathrm{4}}{\pi}\:\left[\frac{\mathrm{2}}{\pi}{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\pi}\:+\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\left(\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\mathrm{1}\right)\:=\frac{\sqrt{\mathrm{2}}}{\pi}\:\:+\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\left(\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{8}\right)\:=\frac{\pi\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{8}}{\pi^{\mathrm{2}} }\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19
![f(x)=xcos(((πx)/2)) f(−x)=(−x)cos(((−πx)/2))=−xcos(((πx)/2)) but ∣−xcos(((πx)/2))∣=xcos(((πx)/2)) ∫_(−(1/2)) ^(1/2) ∣((xcos(((πx)/2)))/)∣=2∫_0 ^(1/2) ∣xcos(((πx)/2))∣ 2×∫_0 ^(1/2) xcos(((πx)/2))dx I_1 =∫xcos(((πx)/2))dx =x×((sin(((πx)/2)))/(π/2))−1×∫((sin(((πx)/2)))/(π/2))dx =((2x)/π)sin(((πx)/2))+(2/π)×((cos(((πx)/2)))/(π/2)) =((2x)/π)sin(((πx)/2))+(4/π^2 )cos(((πx)/2)) required answer is 2×∣((2x)/π)sin(((πx)/2))+(4/π^2 )cos(((πx)/2))∣_0 ^(1/2) =2×[{((2×(1/2))/π)sin((π/4))+(4/π^2 )cos((π/4))}−{0+(4/π^2 )cos0}] =2×[(1/(π(√2)))+(4/(π^2 (√2)))−(4/π^2 )] =((√2)/π)+(8/(π^2 (√2)))−(8/π^2 ) pls check the steps mistake if any](Q53300.png)
$${f}\left({x}\right)={xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right) \\ $$$${f}\left(−{x}\right)=\left(−{x}\right){cos}\left(\frac{−\pi{x}}{\mathrm{2}}\right)=−{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right) \\ $$$${but}\:\mid−{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid={xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right) \\ $$$$\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mid\frac{{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right)}{}\mid=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \mid{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid \\ $$$$\mathrm{2}×\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right){dx} \\ $$$${I}_{\mathrm{1}} =\int{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right){dx} \\ $$$$={x}×\frac{{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)}{\frac{\pi}{\mathrm{2}}}−\mathrm{1}×\int\frac{{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)}{\frac{\pi}{\mathrm{2}}}{dx} \\ $$$$=\frac{\mathrm{2}{x}}{\pi}{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)+\frac{\mathrm{2}}{\pi}×\frac{{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)}{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}{x}}{\pi}{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)+\frac{\mathrm{4}}{\pi^{\mathrm{2}} }{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right) \\ $$$${required}\:{answer}\:{is} \\ $$$$\mathrm{2}×\mid\frac{\mathrm{2}{x}}{\pi}{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)+\frac{\mathrm{4}}{\pi^{\mathrm{2}} }{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}×\left[\left\{\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\pi}{sin}\left(\frac{\pi}{\mathrm{4}}\right)+\frac{\mathrm{4}}{\pi^{\mathrm{2}} }{cos}\left(\frac{\pi}{\mathrm{4}}\right)\right\}−\left\{\mathrm{0}+\frac{\mathrm{4}}{\pi^{\mathrm{2}} }{cos}\mathrm{0}\right\}\right] \\ $$$$=\mathrm{2}×\left[\frac{\mathrm{1}}{\pi\sqrt{\mathrm{2}}}+\frac{\mathrm{4}}{\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}−\frac{\mathrm{4}}{\pi^{\mathrm{2}} }\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\pi}+\frac{\mathrm{8}}{\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}−\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\:{pls}\:{check}\:{the}\:{steps}\:{mistake}\:{if}\:{any} \\ $$
Commented by gunawan last updated on 20/Jan/19

$$\mathrm{Wow} \\ $$$$\mathrm{Ok}\:\mathrm{Sir} \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
