Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 54955 by gunawan last updated on 15/Feb/19

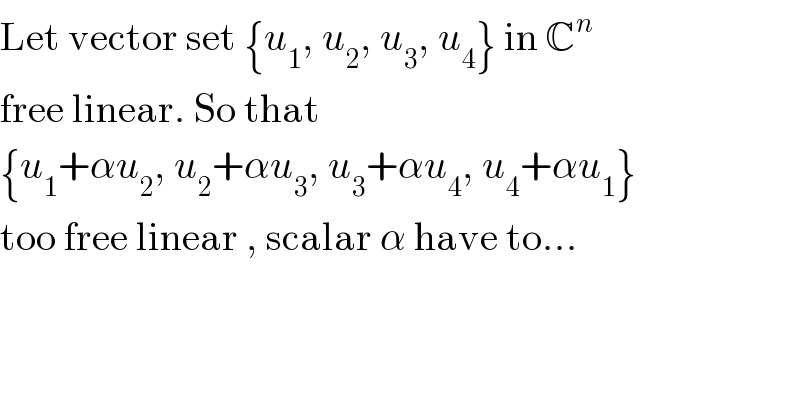
Let vector set {u_1 , u_2 , u_3 , u_4 } in C^n free linear. So that {u_1 +αu_2 , u_2 +αu_3 , u_3 +αu_4 , u_4 +αu_1 } too free linear , scalar α have to...

$$\mathrm{Let}\:\mathrm{vector}\:\mathrm{set}\:\left\{{u}_{\mathrm{1}} ,\:{u}_{\mathrm{2}} ,\:{u}_{\mathrm{3}} ,\:{u}_{\mathrm{4}} \right\}\:\mathrm{in}\:\mathbb{C}^{{n}} \\ $$$$\mathrm{free}\:\mathrm{linear}.\:\mathrm{So}\:\mathrm{that}\: \\ $$$$\left\{{u}_{\mathrm{1}} +\alpha{u}_{\mathrm{2}} ,\:{u}_{\mathrm{2}} +\alpha{u}_{\mathrm{3}} ,\:{u}_{\mathrm{3}} +\alpha{u}_{\mathrm{4}} ,\:{u}_{\mathrm{4}} +\alpha{u}_{\mathrm{1}} \right\} \\ $$$$\mathrm{too}\:\mathrm{free}\:\mathrm{linear}\:,\:\mathrm{scalar}\:\alpha\:\mathrm{have}\:\mathrm{to}... \\ $$

Answered by kaivan.ahmadi last updated on 15/Feb/19

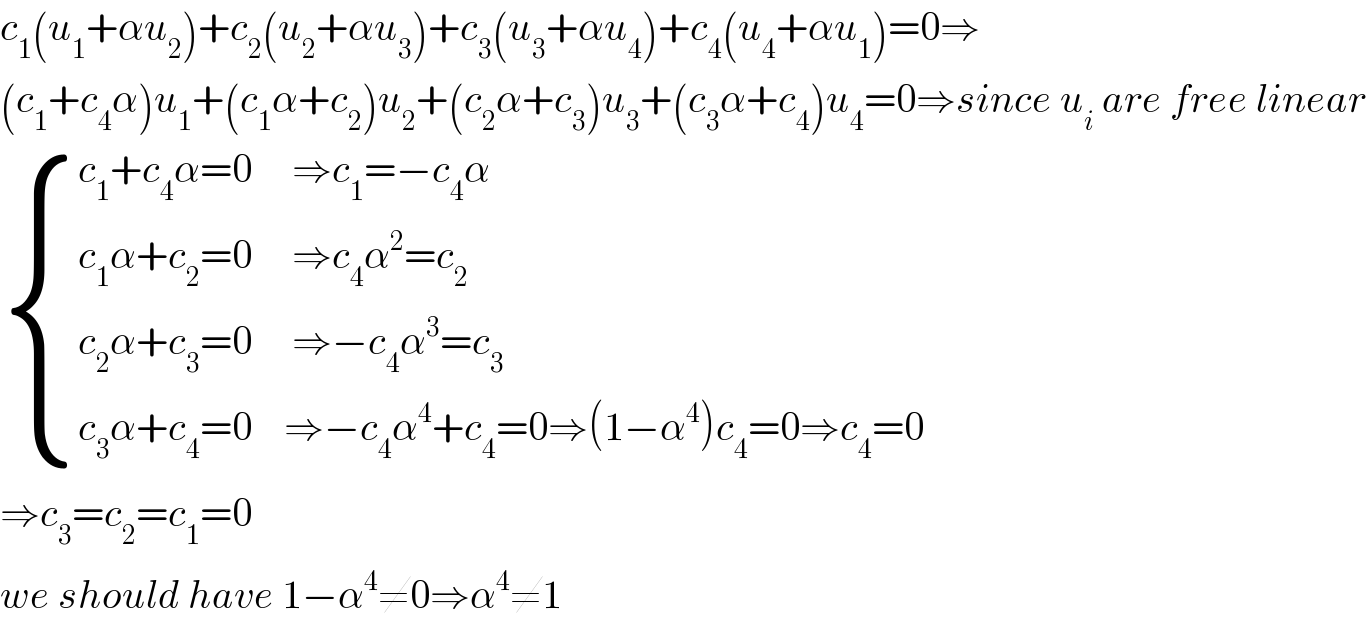
c_1 (u_1 +αu_2 )+c_2 (u_2 +αu_3 )+c_3 (u_3 +αu_4 )+c_4 (u_4 +αu_1 )=0⇒ (c_1 +c_4 α)u_1 +(c_1 α+c_2 )u_2 +(c_2 α+c_3 )u_3 +(c_3 α+c_4 )u_4 =0⇒since u_i are free linear { ((c_1 +c_4 α=0 ⇒c_1 =−c_4 α)),((c_1 α+c_2 =0 ⇒c_4 α^2 =c_2 )),((c_2 α+c_3 =0 ⇒−c_4 α^3 =c_3 )),((c_3 α+c_4 =0 ⇒−c_4 α^4 +c_4 =0⇒(1−α^4 )c_4 =0⇒c_4 =0)) :} ⇒c_3 =c_2 =c_1 =0 we should have 1−α^4 ≠0⇒α^4 ≠1

$${c}_{\mathrm{1}} \left({u}_{\mathrm{1}} +\alpha{u}_{\mathrm{2}} \right)+{c}_{\mathrm{2}} \left({u}_{\mathrm{2}} +\alpha{u}_{\mathrm{3}} \right)+{c}_{\mathrm{3}} \left({u}_{\mathrm{3}} +\alpha{u}_{\mathrm{4}} \right)+{c}_{\mathrm{4}} \left({u}_{\mathrm{4}} +\alpha{u}_{\mathrm{1}} \right)=\mathrm{0}\Rightarrow \\ $$$$\left({c}_{\mathrm{1}} +{c}_{\mathrm{4}} \alpha\right){u}_{\mathrm{1}} +\left({c}_{\mathrm{1}} \alpha+{c}_{\mathrm{2}} \right){u}_{\mathrm{2}} +\left({c}_{\mathrm{2}} \alpha+{c}_{\mathrm{3}} \right){u}_{\mathrm{3}} +\left({c}_{\mathrm{3}} \alpha+{c}_{\mathrm{4}} \right){u}_{\mathrm{4}} =\mathrm{0}\Rightarrow{since}\:{u}_{{i}} \:{are}\:{free}\:{linear} \\ $$$$\begin{cases}{{c}_{\mathrm{1}} +{c}_{\mathrm{4}} \alpha=\mathrm{0}\:\:\:\:\:\Rightarrow{c}_{\mathrm{1}} =−{c}_{\mathrm{4}} \alpha}\\{{c}_{\mathrm{1}} \alpha+{c}_{\mathrm{2}} =\mathrm{0}\:\:\:\:\:\Rightarrow{c}_{\mathrm{4}} \alpha^{\mathrm{2}} ={c}_{\mathrm{2}} }\\{{c}_{\mathrm{2}} \alpha+{c}_{\mathrm{3}} =\mathrm{0}\:\:\:\:\:\Rightarrow−{c}_{\mathrm{4}} \alpha^{\mathrm{3}} ={c}_{\mathrm{3}} }\\{{c}_{\mathrm{3}} \alpha+{c}_{\mathrm{4}} =\mathrm{0}\:\:\:\:\Rightarrow−{c}_{\mathrm{4}} \alpha^{\mathrm{4}} +{c}_{\mathrm{4}} =\mathrm{0}\Rightarrow\left(\mathrm{1}−\alpha^{\mathrm{4}} \right){c}_{\mathrm{4}} =\mathrm{0}\Rightarrow{c}_{\mathrm{4}} =\mathrm{0}}\end{cases} \\ $$$$\Rightarrow{c}_{\mathrm{3}} ={c}_{\mathrm{2}} ={c}_{\mathrm{1}} =\mathrm{0} \\ $$$${we}\:{should}\:{have}\:\mathrm{1}−\alpha^{\mathrm{4}} \neq\mathrm{0}\Rightarrow\alpha^{\mathrm{4}} \neq\mathrm{1} \\ $$

Commented by gunawan last updated on 15/Feb/19

nice thank you Sir

$$\mathrm{nice} \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com