
Question Number 55906 by gunawan last updated on 06/Mar/19
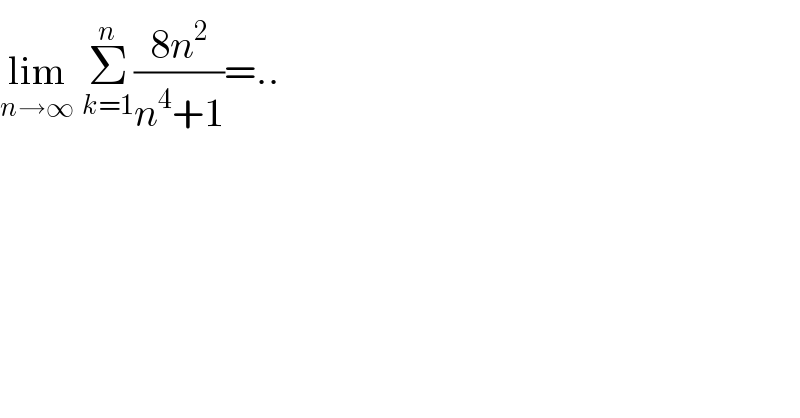
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\overset{{n}} {\underset{{k}=\mathrm{1}} {\sum}}\frac{\mathrm{8}{n}^{\mathrm{2}} }{{n}^{\mathrm{4}} +\mathrm{1}}=.. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19
![T_n =((8n^2 )/(1+n^4 ))=((4×2n^2 )/(1+(n^2 )^2 ))=((4×(2tannθ))/(1+(tannθ)^2 ))=4sin(2nθ) T_1 =4sin(2×1×θ)→(here n^2 =tannθ] T_2 =4sin(2×2×θ) ... ... now S=4[sin2θ+sin4θ+sin6θ+...+sin2nθ] 2sin2θsinθ=cosθ−cos3θ 2sin4θsinθ=cos3θ−cos5θ 2sin6θsinθ=cos5θ−cos7θ .... .... 2sin2nθsinθ=cos(2n−1)θ−cos(2n+1)θ add them 2sinθ[sin2θ+sin4θ+...+sin2nθ]=cosθ−cos(2n+1)θ 2sinθ×(S/4)=2sin(n+1)θsinnθ S=((4sin(n+1)θsin(nθ))/(sinθ)) [ now tannθ=n^2 →sinnθ=(n^2 /(√(1+n^4 ))) cosnθ=(1/(√(1+n^4 ))) sinθ=(1/(√2)) cosθ=(1/(√2)) S=((4[sinnθcosθ+cosnθsinθ]sinnθ)/(sinθ)) S=((4[(n^2 /(√(1+n^4 )))×(1/(√2))+(1/(√(1+n^4 )))×(1/(√2))]×(n^2 /(√(1+n^4 ))))/(1/(√2))) S=4[(n^2 /(n^2 (√((1/n^4 )+1)) ))+(1/(√(1+n^4 )))]×(n^2 /(n^2 (√((1/n^4 )+1)))) when n→∞ S=4[(1/(√(0+1)))+0]×(1/(√(0+1))) so answer is 4 pls check is it correct... i have doubt also becos T_1 it self is 4 ... so how S can be 4... pls pls check the steps mistake if any...](Q55911.png)
$${T}_{{n}} =\frac{\mathrm{8}{n}^{\mathrm{2}} }{\mathrm{1}+{n}^{\mathrm{4}} }=\frac{\mathrm{4}×\mathrm{2}{n}^{\mathrm{2}} }{\mathrm{1}+\left({n}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{4}×\left(\mathrm{2}{tann}\theta\right)}{\mathrm{1}+\left({tann}\theta\right)^{\mathrm{2}} }=\mathrm{4}{sin}\left(\mathrm{2}{n}\theta\right) \\ $$$${T}_{\mathrm{1}} =\mathrm{4}{sin}\left(\mathrm{2}×\mathrm{1}×\theta\right)\rightarrow\left({here}\:{n}^{\mathrm{2}} ={tann}\theta\right] \\ $$$${T}_{\mathrm{2}} =\mathrm{4}{sin}\left(\mathrm{2}×\mathrm{2}×\theta\right) \\ $$$$... \\ $$$$... \\ $$$${now} \\ $$$${S}=\mathrm{4}\left[{sin}\mathrm{2}\theta+{sin}\mathrm{4}\theta+{sin}\mathrm{6}\theta+...+{sin}\mathrm{2}{n}\theta\right] \\ $$$$\mathrm{2}{sin}\mathrm{2}\theta{sin}\theta={cos}\theta−{cos}\mathrm{3}\theta \\ $$$$\mathrm{2}{sin}\mathrm{4}\theta{sin}\theta={cos}\mathrm{3}\theta−{cos}\mathrm{5}\theta \\ $$$$\mathrm{2}{sin}\mathrm{6}\theta{sin}\theta={cos}\mathrm{5}\theta−{cos}\mathrm{7}\theta \\ $$$$.... \\ $$$$.... \\ $$$$\mathrm{2}{sin}\mathrm{2}{n}\theta{sin}\theta={cos}\left(\mathrm{2}{n}−\mathrm{1}\right)\theta−{cos}\left(\mathrm{2}{n}+\mathrm{1}\right)\theta \\ $$$${add}\:{them} \\ $$$$\mathrm{2}{sin}\theta\left[{sin}\mathrm{2}\theta+{sin}\mathrm{4}\theta+...+{sin}\mathrm{2}{n}\theta\right]={cos}\theta−{cos}\left(\mathrm{2}{n}+\mathrm{1}\right)\theta \\ $$$$\mathrm{2}{sin}\theta×\frac{{S}}{\mathrm{4}}=\mathrm{2}{sin}\left({n}+\mathrm{1}\right)\theta{sinn}\theta \\ $$$${S}=\frac{\mathrm{4}{sin}\left({n}+\mathrm{1}\right)\theta{sin}\left({n}\theta\right)}{{sin}\theta} \\ $$$$\left[\right. \\ $$$${now}\:{tann}\theta={n}^{\mathrm{2}} \rightarrow{sinn}\theta=\frac{{n}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{n}^{\mathrm{4}} }} \\ $$$${cosn}\theta=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{n}^{\mathrm{4}} }} \\ $$$${sin}\theta=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\:{cos}\theta=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$${S}=\frac{\mathrm{4}\left[{sinn}\theta{cos}\theta+{cosn}\theta{sin}\theta\right]{sinn}\theta}{{sin}\theta} \\ $$$${S}=\frac{\mathrm{4}\left[\frac{{n}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{n}^{\mathrm{4}} }}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{n}^{\mathrm{4}} }}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right]×\frac{{n}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{n}^{\mathrm{4}} }}}{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \\ $$$${S}=\mathrm{4}\left[\frac{{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}}{{n}^{\mathrm{4}} }+\mathrm{1}}\:}+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{n}^{\mathrm{4}} }}\right]×\frac{{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}}{{n}^{\mathrm{4}} }+\mathrm{1}}} \\ $$$$ \\ $$$${when}\:{n}\rightarrow\infty \\ $$$${S}=\mathrm{4}\left[\frac{\mathrm{1}}{\sqrt{\mathrm{0}+\mathrm{1}}}+\mathrm{0}\right]×\frac{\mathrm{1}}{\sqrt{\mathrm{0}+\mathrm{1}}} \\ $$$${so}\:{answer}\:{is}\:\mathrm{4} \\ $$$${pls}\:{check}\:{is}\:{it}\:{correct}...\:{i}\:{have}\:{doubt}\:{also} \\ $$$${becos}\:{T}_{\mathrm{1}} \:{it}\:{self}\:{is}\:\mathrm{4}\:... \\ $$$${so}\:\:{how}\:{S}\:{can}\:{be}\:\mathrm{4}... \\ $$$${pls}\:{pls}\:{check}\:{the}\:{steps}\:{mistake}\:{if}\:{any}... \\ $$
Commented by mr W last updated on 06/Mar/19
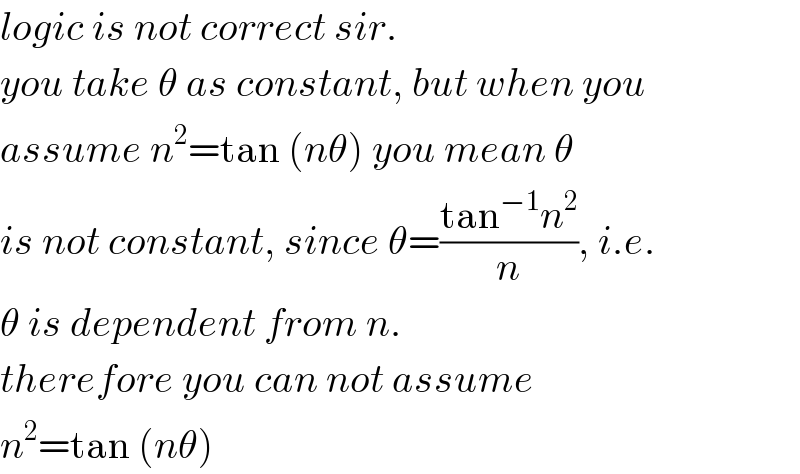
$${logic}\:{is}\:{not}\:{correct}\:{sir}. \\ $$$${you}\:{take}\:\theta\:{as}\:{constant},\:{but}\:{when}\:{you} \\ $$$${assume}\:{n}^{\mathrm{2}} =\mathrm{tan}\:\left({n}\theta\right)\:{you}\:{mean}\:\theta \\ $$$${is}\:{not}\:{constant},\:{since}\:\theta=\frac{\mathrm{tan}^{−\mathrm{1}} {n}^{\mathrm{2}} }{{n}},\:{i}.{e}. \\ $$$$\theta\:{is}\:{dependent}\:{from}\:{n}. \\ $$$${therefore}\:{you}\:{can}\:{not}\:{assume} \\ $$$${n}^{\mathrm{2}} =\mathrm{tan}\:\left({n}\theta\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19

$${thank}\:{you}\:{sir}... \\ $$
Commented by mr W last updated on 06/Mar/19
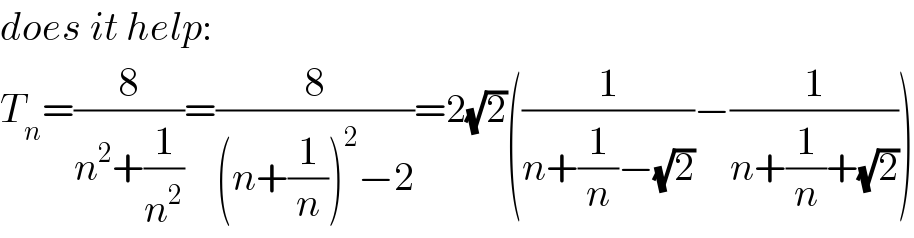
$${does}\:{it}\:{help}: \\ $$$${T}_{{n}} =\frac{\mathrm{8}}{{n}^{\mathrm{2}} +\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}=\frac{\mathrm{8}}{\left({n}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} −\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{{n}}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{{n}}+\sqrt{\mathrm{2}}}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19
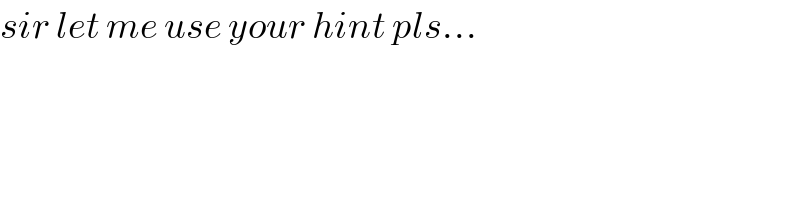
$${sir}\:{let}\:{me}\:{use}\:{your}\:{hint}\:{pls}... \\ $$
