
Question Number 58500 by Kunal12588 last updated on 24/Apr/19

$${change}\:{in}\:{simplest}\:{form}\:: \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Answered by MJS last updated on 24/Apr/19

$$\frac{\sqrt{{a}}+\sqrt{{b}}}{\sqrt{{a}}−\sqrt{{b}}}=\frac{\left(\sqrt{{a}}+\sqrt{{b}}\right)^{\mathrm{2}} }{\left(\sqrt{{a}}−\sqrt{{b}}\right)\left(\sqrt{{a}}+\sqrt{{b}}\right)}=\frac{{a}+\mathrm{2}\sqrt{{ab}}+{b}}{{a}−{b}} \\ $$$$\frac{\mathrm{1}+{x}^{\mathrm{2}} +\mathrm{2}\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}+\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} −\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}= \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{arctan}\:\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{{x}^{\mathrm{2}} }\:={t} \\ $$$$\Rightarrow\:{x}=\pm\sqrt{\mathrm{sin}\:\mathrm{2}{t}}\:\Rightarrow\:{t}=\frac{\mathrm{2}{n}\pi+\mathrm{arcsin}\:{x}^{\mathrm{2}} }{\mathrm{2}}\:\vee\:{t}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\mathrm{arcsin}\:{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{testing}\:\mathrm{values}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{arctan}\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\frac{\pi−\mathrm{arcsin}\:{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by Kunal12588 last updated on 24/Apr/19
$${thank}\:{you}\:{sir},\:{I}\:{have}\:{also}\:{written}\:{an}\:{ans} \\ $$$${pls}\:{check}. \\ $$
Answered by Kunal12588 last updated on 24/Apr/19

$${tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${let}\:{x}^{\mathrm{2}} ={cos}\:{y} \\ $$$$\Rightarrow{cos}^{−\mathrm{1}} {x}^{\mathrm{2}} ={y} \\ $$$${tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}+{cos}\:{y}}+\sqrt{\mathrm{1}−{cos}\:{y}}}{\sqrt{\mathrm{1}+{cos}\:{y}}−\sqrt{\mathrm{1}−{cos}\:{y}}} \\ $$$$={tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}{cos}\frac{{y}}{\mathrm{2}}+\sqrt{\mathrm{2}}{sin}\frac{{y}}{\mathrm{2}}}{\sqrt{\mathrm{2}}{cos}\frac{{y}}{\mathrm{2}}−\sqrt{\mathrm{2}}{sin}\frac{{y}}{\mathrm{2}}} \\ $$$$={tan}^{−\mathrm{1}} \frac{\mathrm{1}+{tan}\frac{{y}}{\mathrm{2}}}{\mathrm{1}−{tan}\frac{{y}}{\mathrm{2}}} \\ $$$$={tan}^{−\mathrm{1}} \frac{{tan}\frac{\pi}{\mathrm{4}}+{tan}\frac{{y}}{\mathrm{2}}}{\mathrm{1}−{tan}\frac{\pi}{\mathrm{4}}{tan}\frac{{y}}{\mathrm{2}}} \\ $$$$={tan}^{−\mathrm{1}} \left({tan}\left(\frac{\pi}{\mathrm{4}}+\frac{{y}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{{y}}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{cos}^{−\mathrm{1}} {x}^{\mathrm{2}} \: \\ $$
Commented by MJS last updated on 24/Apr/19
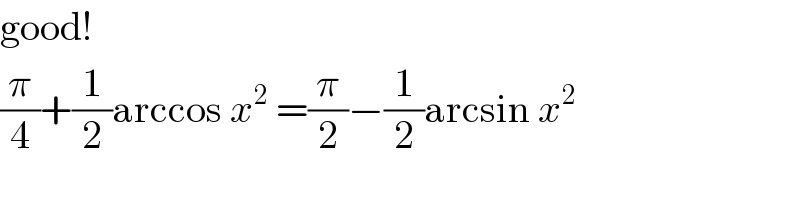
$$\mathrm{good}! \\ $$$$\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arccos}\:{x}^{\mathrm{2}} \:=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arcsin}\:{x}^{\mathrm{2}} \\ $$
