Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 59893 by aliesam last updated on 15/May/19

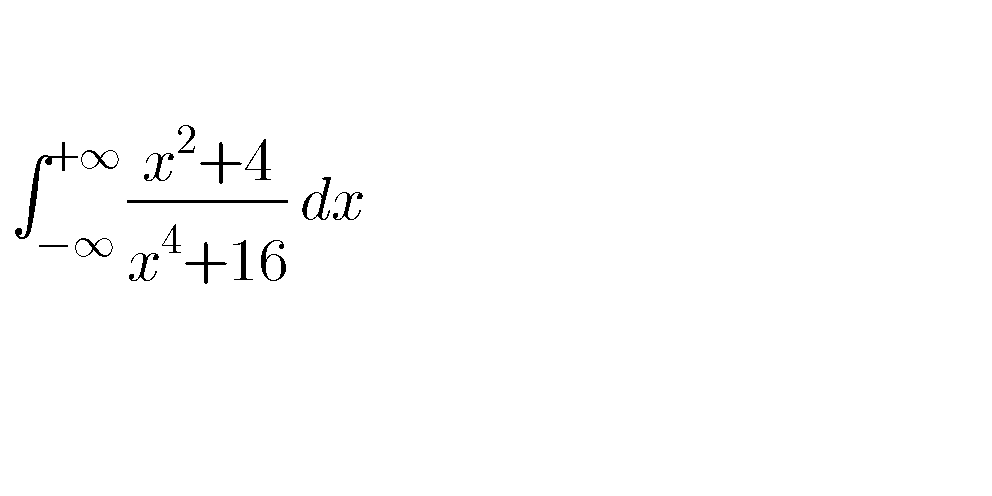
Commented by maxmathsup by imad last updated on 15/May/19

method using the formuae ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) if 0<a<1 let I =∫_(−∞) ^(+∞) ((x^2 +4)/(x^4 +16)) ⇒I =_(x=2t) ∫_(−∞) ^(+∞) ((4t^2 +4)/(16t^4 +16)) (2)dt =(1/2) ∫_(−∞) ^(+∞) ((t^2 +1)/(t^4 +1)) dt =∫_0 ^∞ ((t^2 +1)/(t^4 +1)) dt =∫_0 ^∞ (t^2 /(t^4 +1)) dt +∫_0 ^∞ (dt/(t^4 +1)) changement t^4 =u give t =u^(1/4) ⇒∫_0 ^∞ (t^2 /(t^4 +1)) dt =∫_0 ^∞ (u^(1/2) /(1+u)) (1/4)u^((1/4)−1) du =(1/4) ∫_0 ^∞ (u^((3/4)−1) /(1+u)) du =(1/4) (π/(sin(((3π)/4)))) =(π/(4.(1/(√2)))) =((π(√2))/4) same changement give ∫_0 ^∞ (dt/(1+t^4 )) =∫_0 ^∞ (1/4) (u^((1/4)−1) /(1+u)) du =(1/4) (π/(sin((π/4)))) =(π/(4(1/(√2)))) =((π(√2))/4) ⇒ I =((π(√2))/4) +((π(√2))/4) = ((2π(√2))/4) =((π(√2))/2) ⇒ ★ I =(π/(√2)) ★

$${method}\:{using}\:{the}\:{formuae}\:\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:\:{if}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$${let}\:{I}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{4}}{{x}^{\mathrm{4}} \:+\mathrm{16}}\:\Rightarrow{I}\:=_{{x}=\mathrm{2}{t}} \:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{4}}{\mathrm{16}{t}^{\mathrm{4}} \:+\mathrm{16}}\:\left(\mathrm{2}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:+\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{{t}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$${changement}\:\:\:{t}^{\mathrm{4}} \:={u}\:\:{give}\:{t}\:={u}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{u}}\:\frac{\mathrm{1}}{\mathrm{4}}{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}^{\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}.\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${same}\:{changement}\:{give}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{I}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:+\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\:\frac{\mathrm{2}\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\Rightarrow\:\bigstar\:{I}\:=\frac{\pi}{\sqrt{\mathrm{2}}}\:\bigstar \\ $$

Commented by malwaan last updated on 15/May/19

great sir but ; can anyone solve it without using this formulae

$${great}\:{sir} \\ $$$${but}\:;\:{can}\:{anyone}\:{solve}\:{it} \\ $$$${without}\:{using}\:{this}\:{formulae} \\ $$

Commented by maxmathsup by imad last updated on 16/May/19

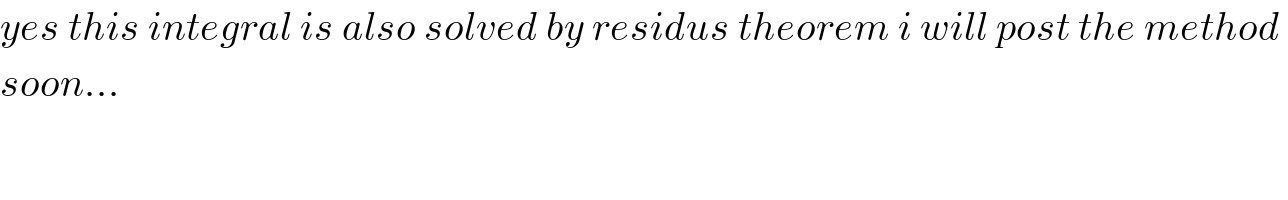
yes this integral is also solved by residus theorem i will post the method soon...

$${yes}\:{this}\:{integral}\:{is}\:{also}\:{solved}\:{by}\:{residus}\:{theorem}\:{i}\:{will}\:{post}\:{the}\:{method}\: \\ $$$${soon}... \\ $$

Commented by malwaan last updated on 16/May/19

thanks sir I am waiting ...

$${thanks}\:{sir}\: \\ $$$${I}\:{am}\:{waiting}\:... \\ $$

Commented by maxmathsup by imad last updated on 17/May/19

residus method let A =∫_(−∞) ^(+∞) ((x^2 +4)/(x^4 +16))dx ⇒A=_(x=2t) ∫_(−∞) ^(+∞) ((4t^2 +4)/(16(t^4 +1)))2dt ⇒2A =∫_(−∞) ^(+∞) ((t^2 +1)/(t^4 +1)) dt let W(z) = ((z^2 +1)/(z^4 +1)) poles of W! W(z) =((z^2 +1)/((z^2 −i)(z^2 +i))) =((z^2 +1)/((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) so the poles of W are +^− e^((iπ)/4) and +^− e^(−((iπ)/4)) residus theorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ{ Res(W,e^((iπ)/4) ) +Res(W,−e^(−((iπ)/4)) )} Res(W,e^((iπ)/4) ) =lim_(z→e^((iπ)/4) ) (z−e^((iπ)/4) )W(z) = ((i+1)/(2e^((iπ)/4) (2i))) =((1+i)/(4i )) e^(−((iπ)/4)) Res(W,−e^(−((iπ)/4)) ) =lim_(z→−e^(−((iπ)/4)) ) (z+e^(−((iπ)/4)) )W(z) = ((−i+1)/(−2e^(−((iπ)/4)) (−2i))) =(((1−i)e^((iπ)/4) )/(4i)) ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ(((1+i)/(4i)) e^(−((iπ)/4)) +((1−i)/(4i)) e^((iπ)/4) } =(π/2) ( 2Re(1+i)e^(−((iπ)/4)) ) =π Re{ (1+i)e^(−((iπ)/4)) } but (1+i)e^(−i(π/4)) =(√2)e^((iπ)/4) e^(−((iπ)/4)) =(√2) ⇒∫_(−∞) ^(+∞) W(z)dz =π(√(2 )) ⇒ 2A =π(√2) ⇒ A =((π(√2))/2) ⇒ A =(π/(√2)) .

$${residus}\:{method}\:{let}\:\:{A}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{4}}{{x}^{\mathrm{4}} \:+\mathrm{16}}{dx}\:\Rightarrow{A}=_{{x}=\mathrm{2}{t}} \:\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{4}}{\mathrm{16}\left({t}^{\mathrm{4}} \:+\mathrm{1}\right)}\mathrm{2}{dt} \\ $$$$\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:\:{let}\:{W}\left({z}\right)\:=\:\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{4}} \:+\mathrm{1}}\:\:\:{poles}\:{of}\:{W}! \\ $$$${W}\left({z}\right)\:=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)}\:=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:\:{so}\:{the}\:{poles}\:{of}\:{W} \\ $$$${are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:{and}\:\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right){W}\left({z}\right)\:=\:\frac{{i}+\mathrm{1}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{\mathrm{1}+{i}}{\mathrm{4}{i}\:}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$${Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow−{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right){W}\left({z}\right)\:=\:\frac{−{i}+\mathrm{1}}{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\left(−\mathrm{2}{i}\right)}\:=\frac{\left(\mathrm{1}−{i}\right){e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left(\frac{\mathrm{1}+{i}}{\mathrm{4}{i}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:+\frac{\mathrm{1}−{i}}{\mathrm{4}{i}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right\}\:=\frac{\pi}{\mathrm{2}}\:\left(\:\mathrm{2}{Re}\left(\mathrm{1}+{i}\right){e}^{−\frac{{i}\pi}{\mathrm{4}}} \right) \\ $$$$=\pi\:{Re}\left\{\:\left(\mathrm{1}+{i}\right){e}^{−\frac{{i}\pi}{\mathrm{4}}} \right\}\:{but}\:\:\left(\mathrm{1}+{i}\right){e}^{−{i}\frac{\pi}{\mathrm{4}}} \:=\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:=\sqrt{\mathrm{2}}\:\Rightarrow\int_{−\infty} ^{+\infty} {W}\left({z}\right){dz}\:=\pi\sqrt{\mathrm{2}\:}\:\Rightarrow \\ $$$$\mathrm{2}{A}\:=\pi\sqrt{\mathrm{2}}\:\Rightarrow\:{A}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\:{A}\:=\frac{\pi}{\sqrt{\mathrm{2}}}\:. \\ $$

Commented by malwaan last updated on 18/May/19

Thank you so much sir

$${Thank}\:{you}\:{so}\:{much}\:{sir} \\ $$

Commented by maxmathsup by imad last updated on 18/May/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com