Question Number 59992 by ajfour last updated on 16/May/19
Commented by ajfour last updated on 16/May/19
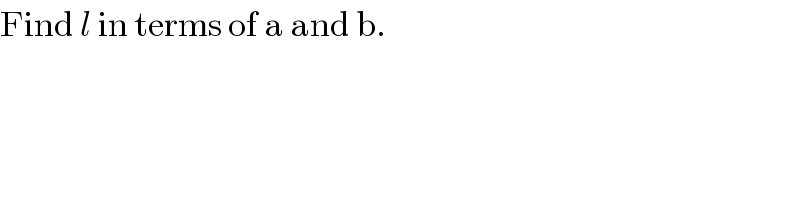
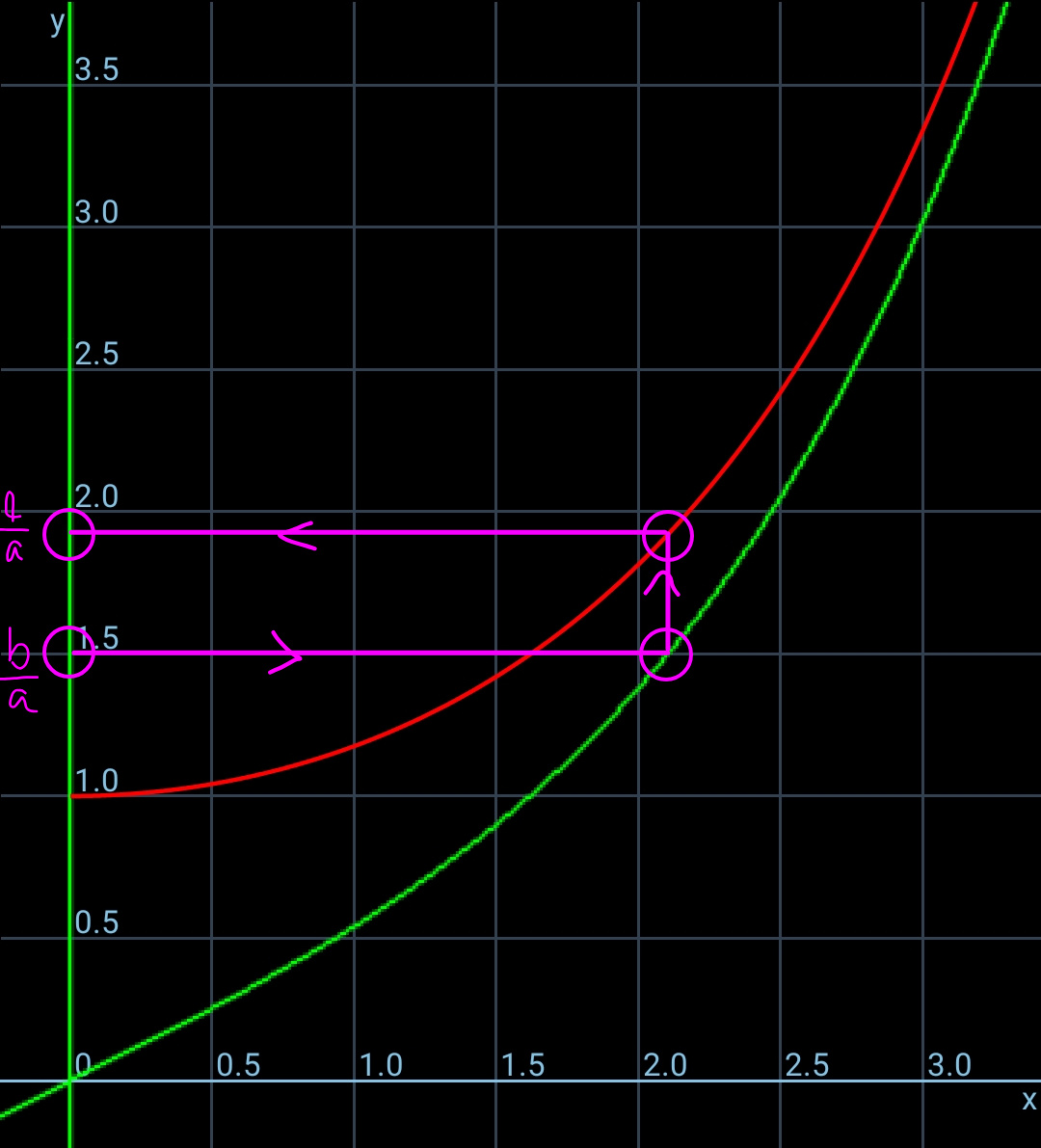
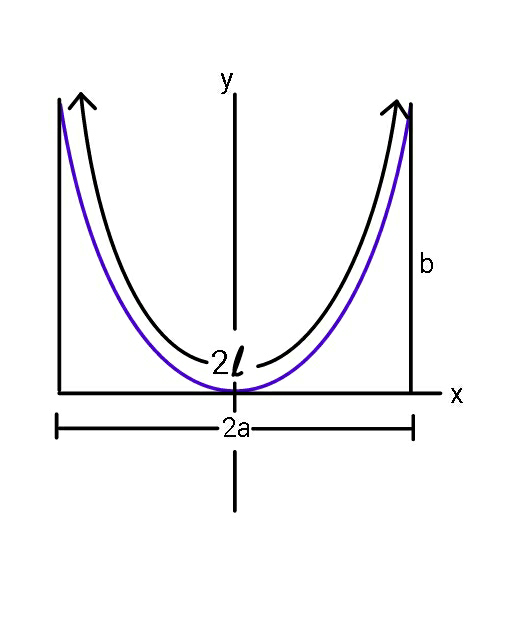
$$\mathrm{Find}\:{l}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}. \\ $$
Answered by ajfour last updated on 16/May/19
![y=Ax^2 b=Aa^2 ⇒ A=(b/a^2 ) y=((bx^2 )/a^2 ) (dy/dx)=((2bx)/a^2 ) = tan θ ⇒ dx=(a^2 /(2b))sec^2 θdθ l =∫_0 ^( a) (√(1+((4b^2 x^2 )/a^4 )))dx = ((2b)/a^2 )∫_0 ^( a) (√(((a^2 /(2b)))^2 +x^2 )) dx = ((2b)/a^2 ){(x/2)(√(((a^2 /(2b)))^2 +x^2 ))+(1/2)((a^2 /(2b)))^2 ln ∣x+(√(((a^2 /(2b)))^2 +x^2 )) ∣} l=(b/a)(√(((a^2 /(2b)))^2 +a^2 ))+(a^2 /(4b))ln (((a+(√(((a^2 /(2b)))^2 +a^2 )))/(a^2 /(2b)))) l= (a/2)[(√5)+(a/(2b))ln {((2b)/a)+(√(1+(((2b)/a))^2 )) }] If a=b=1 l=((√5)/2)+(1/4)ln (2+(√5)) .](Q59995.png)
$$\:\:\mathrm{y}=\mathrm{Ax}^{\mathrm{2}} \\ $$$$\:\mathrm{b}=\mathrm{Aa}^{\mathrm{2}} \:\:\Rightarrow\:\:\mathrm{A}=\frac{\mathrm{b}}{\mathrm{a}^{\mathrm{2}} } \\ $$$$\:\:\mathrm{y}=\frac{\mathrm{bx}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{2bx}}{\mathrm{a}^{\mathrm{2}} }\:=\:\mathrm{tan}\:\theta\:\:\:\Rightarrow\:\:\mathrm{dx}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2b}}\mathrm{sec}\:^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:{l}\:=\int_{\mathrm{0}} ^{\:\:\mathrm{a}} \sqrt{\mathrm{1}+\frac{\mathrm{4b}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{4}} }}\mathrm{dx} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{2b}}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\:\mathrm{a}} \sqrt{\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2b}}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\:\:\:\:=\:\frac{\mathrm{2b}}{\mathrm{a}^{\mathrm{2}} }\left\{\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2b}}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2b}}\right)^{\mathrm{2}} \mathrm{ln}\:\mid\mathrm{x}+\sqrt{\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2b}}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }\:\mid\right\} \\ $$$$\:\:\boldsymbol{{l}}=\frac{{b}}{{a}}\sqrt{\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}{b}}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{4}{b}}\mathrm{ln}\:\left(\frac{{a}+\sqrt{\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}{b}}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} }}{\frac{{a}^{\mathrm{2}} }{\mathrm{2}{b}}}\right)\: \\ $$$$\:\:\boldsymbol{{l}}=\:\frac{{a}}{\mathrm{2}}\left[\sqrt{\mathrm{5}}+\frac{{a}}{\mathrm{2}{b}}\mathrm{ln}\:\left\{\frac{\mathrm{2}{b}}{{a}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{b}}{{a}}\right)^{\mathrm{2}} }\:\right\}\right] \\ $$$$\:\mathrm{If}\:\mathrm{a}=\mathrm{b}=\mathrm{1}\:\:\: \\ $$$$\:\:{l}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\:. \\ $$
Commented by mr W last updated on 17/May/19
$${rope}\:{as}\:{catenary}: \\ $$$${y}={k}\:\mathrm{cosh}\:\frac{{x}}{{k}} \\ $$$${b}+{k}={k}\:\mathrm{cosh}\:\frac{{a}}{{k}} \\ $$$$\Rightarrow\frac{{b}}{{a}}×\frac{{a}}{{k}}=\mathrm{cosh}\:\frac{{a}}{{k}}−\mathrm{1} \\ $$$${with}\:\lambda=\frac{{b}}{{a}},\:\mu=\frac{{a}}{{k}} \\ $$$$\Rightarrow\lambda\mu=\mathrm{cosh}\:\mu−\mathrm{1}\:\:...\left({i}\right) \\ $$$${l}={k}\:\mathrm{sinh}\:\frac{{a}}{{k}}={a}\frac{\mathrm{sinh}\:\frac{{a}}{{k}}}{\frac{{a}}{{k}}}={a}\frac{\mathrm{sinh}\:\mu}{\mu} \\ $$$$\Rightarrow\frac{{l}}{{a}}=\frac{\mathrm{sinh}\:\mu}{\mu}\:\:\:...\left({ii}\right) \\ $$
Commented by mr W last updated on 17/May/19

$${very}\:{nice}\:{sir}! \\ $$$${if}\:{the}\:{rope}\:{has}\:{the}\:{form}\:{of}\:{catenary}, \\ $$$${its}\:{length}\:{l}\:{can}\:{not}\:{be}\:{so}\:{explicitly}\: \\ $$$${expressed}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$
Commented by mr W last updated on 17/May/19