Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 6043 by shaikreshma last updated on 10/Jun/16

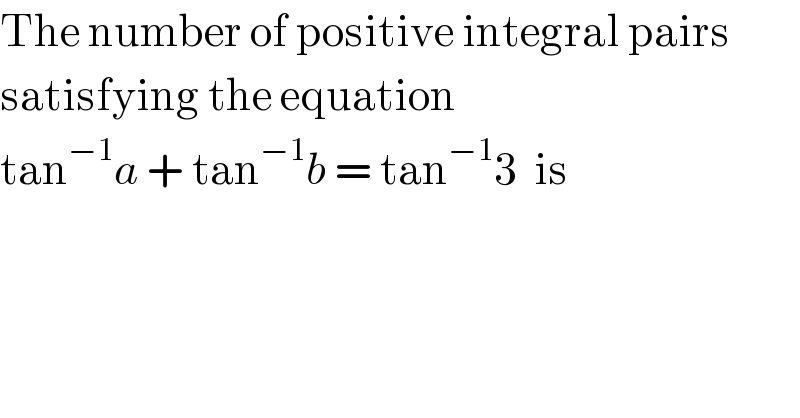
The number of positive integral pairs satisfying the equation tan^(−1) a + tan^(−1) b = tan^(−1) 3 is

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integral}\:\mathrm{pairs} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {a}\:+\:\mathrm{tan}^{−\mathrm{1}} {b}\:=\:\mathrm{tan}^{−\mathrm{1}} \mathrm{3}\:\:\mathrm{is} \\ $$

Answered by Yozzii last updated on 11/Jun/16

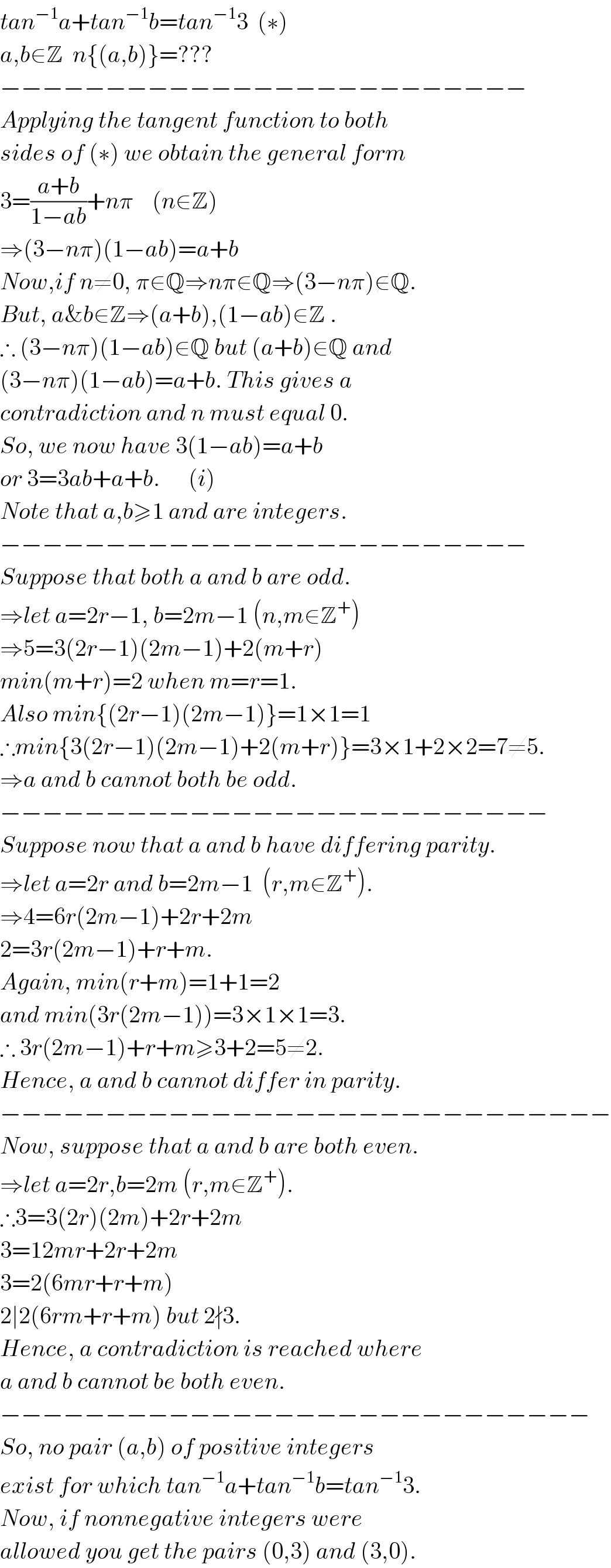
tan^(−1) a+tan^(−1) b=tan^(−1) 3 (∗) a,b∈Z n{(a,b)}=??? −−−−−−−−−−−−−−−−−−−−−−−−− Applying the tangent function to both sides of (∗) we obtain the general form 3=((a+b)/(1−ab))+nπ (n∈Z) ⇒(3−nπ)(1−ab)=a+b Now,if n≠0, π∉Q⇒nπ∉Q⇒(3−nπ)∉Q. But, a&b∈Z⇒(a+b),(1−ab)∈Z . ∴ (3−nπ)(1−ab)∉Q but (a+b)∈Q and (3−nπ)(1−ab)=a+b. This gives a contradiction and n must equal 0. So, we now have 3(1−ab)=a+b or 3=3ab+a+b. (i) Note that a,b≥1 and are integers. −−−−−−−−−−−−−−−−−−−−−−−−− Suppose that both a and b are odd. ⇒let a=2r−1, b=2m−1 (n,m∈Z^+ ) ⇒5=3(2r−1)(2m−1)+2(m+r) min(m+r)=2 when m=r=1. Also min{(2r−1)(2m−1)}=1×1=1 ∴min{3(2r−1)(2m−1)+2(m+r)}=3×1+2×2=7≠5. ⇒a and b cannot both be odd. −−−−−−−−−−−−−−−−−−−−−−−−−− Suppose now that a and b have differing parity. ⇒let a=2r and b=2m−1 (r,m∈Z^+ ). ⇒4=6r(2m−1)+2r+2m 2=3r(2m−1)+r+m. Again, min(r+m)=1+1=2 and min(3r(2m−1))=3×1×1=3. ∴ 3r(2m−1)+r+m≥3+2=5≠2. Hence, a and b cannot differ in parity. −−−−−−−−−−−−−−−−−−−−−−−−−−−−− Now, suppose that a and b are both even. ⇒let a=2r,b=2m (r,m∈Z^+ ). ∴3=3(2r)(2m)+2r+2m 3=12mr+2r+2m 3=2(6mr+r+m) 2∣2(6rm+r+m) but 2∤3. Hence, a contradiction is reached where a and b cannot be both even. −−−−−−−−−−−−−−−−−−−−−−−−−−−− So, no pair (a,b) of positive integers exist for which tan^(−1) a+tan^(−1) b=tan^(−1) 3. Now, if nonnegative integers were allowed you get the pairs (0,3) and (3,0).

$${tan}^{−\mathrm{1}} {a}+{tan}^{−\mathrm{1}} {b}={tan}^{−\mathrm{1}} \mathrm{3}\:\:\left(\ast\right) \\ $$$${a},{b}\in\mathbb{Z}\:\:{n}\left\{\left({a},{b}\right)\right\}=??? \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Applying}\:{the}\:{tangent}\:{function}\:{to}\:{both} \\ $$$${sides}\:{of}\:\left(\ast\right)\:{we}\:{obtain}\:{the}\:{general}\:{form} \\ $$$$\mathrm{3}=\frac{{a}+{b}}{\mathrm{1}−{ab}}+{n}\pi\:\:\:\:\left({n}\in\mathbb{Z}\right) \\ $$$$\Rightarrow\left(\mathrm{3}−{n}\pi\right)\left(\mathrm{1}−{ab}\right)={a}+{b} \\ $$$${Now},{if}\:{n}\neq\mathrm{0},\:\pi\notin\mathbb{Q}\Rightarrow{n}\pi\notin\mathbb{Q}\Rightarrow\left(\mathrm{3}−{n}\pi\right)\notin\mathbb{Q}. \\ $$$${But},\:{a\&b}\in\mathbb{Z}\Rightarrow\left({a}+{b}\right),\left(\mathrm{1}−{ab}\right)\in\mathbb{Z}\:. \\ $$$$\therefore\:\left(\mathrm{3}−{n}\pi\right)\left(\mathrm{1}−{ab}\right)\notin\mathbb{Q}\:{but}\:\left({a}+{b}\right)\in\mathbb{Q}\:{and} \\ $$$$\left(\mathrm{3}−{n}\pi\right)\left(\mathrm{1}−{ab}\right)={a}+{b}.\:{This}\:{gives}\:{a}\: \\ $$$${contradiction}\:{and}\:{n}\:{must}\:{equal}\:\mathrm{0}. \\ $$$${So},\:{we}\:{now}\:{have}\:\mathrm{3}\left(\mathrm{1}−{ab}\right)={a}+{b} \\ $$$${or}\:\mathrm{3}=\mathrm{3}{ab}+{a}+{b}.\:\:\:\:\:\:\left({i}\right) \\ $$$${Note}\:{that}\:{a},{b}\geqslant\mathrm{1}\:{and}\:{are}\:{integers}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{that}\:{both}\:{a}\:{and}\:{b}\:{are}\:{odd}. \\ $$$$\Rightarrow{let}\:{a}=\mathrm{2}{r}−\mathrm{1},\:{b}=\mathrm{2}{m}−\mathrm{1}\:\left({n},{m}\in\mathbb{Z}^{+} \right) \\ $$$$\Rightarrow\mathrm{5}=\mathrm{3}\left(\mathrm{2}{r}−\mathrm{1}\right)\left(\mathrm{2}{m}−\mathrm{1}\right)+\mathrm{2}\left({m}+{r}\right) \\ $$$${min}\left({m}+{r}\right)=\mathrm{2}\:{when}\:{m}={r}=\mathrm{1}. \\ $$$${Also}\:{min}\left\{\left(\mathrm{2}{r}−\mathrm{1}\right)\left(\mathrm{2}{m}−\mathrm{1}\right)\right\}=\mathrm{1}×\mathrm{1}=\mathrm{1} \\ $$$$\therefore{min}\left\{\mathrm{3}\left(\mathrm{2}{r}−\mathrm{1}\right)\left(\mathrm{2}{m}−\mathrm{1}\right)+\mathrm{2}\left({m}+{r}\right)\right\}=\mathrm{3}×\mathrm{1}+\mathrm{2}×\mathrm{2}=\mathrm{7}\neq\mathrm{5}. \\ $$$$\Rightarrow{a}\:{and}\:{b}\:{cannot}\:{both}\:{be}\:{odd}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{now}\:{that}\:{a}\:{and}\:{b}\:{have}\:{differing}\:{parity}. \\ $$$$\Rightarrow{let}\:{a}=\mathrm{2}{r}\:{and}\:{b}=\mathrm{2}{m}−\mathrm{1}\:\:\left({r},{m}\in\mathbb{Z}^{+} \right). \\ $$$$\Rightarrow\mathrm{4}=\mathrm{6}{r}\left(\mathrm{2}{m}−\mathrm{1}\right)+\mathrm{2}{r}+\mathrm{2}{m} \\ $$$$\mathrm{2}=\mathrm{3}{r}\left(\mathrm{2}{m}−\mathrm{1}\right)+{r}+{m}. \\ $$$${Again},\:{min}\left({r}+{m}\right)=\mathrm{1}+\mathrm{1}=\mathrm{2}\: \\ $$$${and}\:{min}\left(\mathrm{3}{r}\left(\mathrm{2}{m}−\mathrm{1}\right)\right)=\mathrm{3}×\mathrm{1}×\mathrm{1}=\mathrm{3}. \\ $$$$\therefore\:\mathrm{3}{r}\left(\mathrm{2}{m}−\mathrm{1}\right)+{r}+{m}\geqslant\mathrm{3}+\mathrm{2}=\mathrm{5}\neq\mathrm{2}. \\ $$$${Hence},\:{a}\:{and}\:{b}\:{cannot}\:{differ}\:{in}\:{parity}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Now},\:{suppose}\:{that}\:{a}\:{and}\:{b}\:{are}\:{both}\:{even}. \\ $$$$\Rightarrow{let}\:{a}=\mathrm{2}{r},{b}=\mathrm{2}{m}\:\left({r},{m}\in\mathbb{Z}^{+} \right). \\ $$$$\therefore\mathrm{3}=\mathrm{3}\left(\mathrm{2}{r}\right)\left(\mathrm{2}{m}\right)+\mathrm{2}{r}+\mathrm{2}{m} \\ $$$$\mathrm{3}=\mathrm{12}{mr}+\mathrm{2}{r}+\mathrm{2}{m} \\ $$$$\mathrm{3}=\mathrm{2}\left(\mathrm{6}{mr}+{r}+{m}\right) \\ $$$$\mathrm{2}\mid\mathrm{2}\left(\mathrm{6}{rm}+{r}+{m}\right)\:{but}\:\mathrm{2}\nmid\mathrm{3}. \\ $$$${Hence},\:{a}\:{contradiction}\:{is}\:{reached}\:{where} \\ $$$${a}\:{and}\:{b}\:{cannot}\:{be}\:{both}\:{even}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${So},\:{no}\:{pair}\:\left({a},{b}\right)\:{of}\:{positive}\:{integers} \\ $$$${exist}\:{for}\:{which}\:{tan}^{−\mathrm{1}} {a}+{tan}^{−\mathrm{1}} {b}={tan}^{−\mathrm{1}} \mathrm{3}. \\ $$$${Now},\:{if}\:{nonnegative}\:{integers}\:{were} \\ $$$${allowed}\:{you}\:{get}\:{the}\:{pairs}\:\left(\mathrm{0},\mathrm{3}\right)\:{and}\:\left(\mathrm{3},\mathrm{0}\right). \\ $$

Commented by Rasheed Soomro last updated on 12/Jun/16

NICE!

$$\mathfrak{NICE}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com