Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62335 by maxmathsup by imad last updated on 19/Jun/19

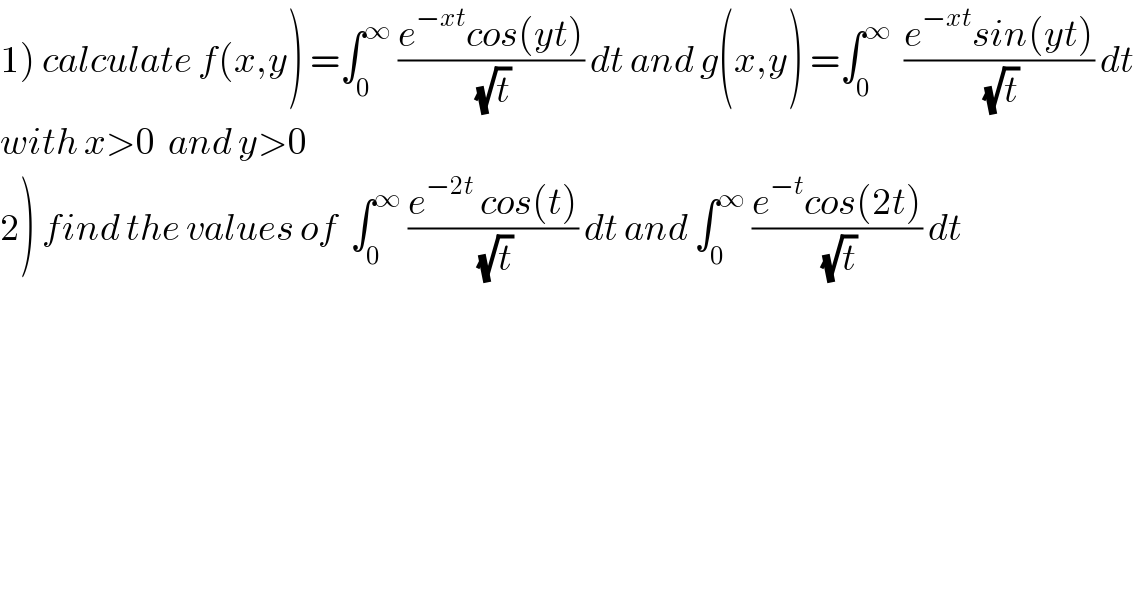
1) calculate f(x,y) =∫_0 ^∞ ((e^(−xt) cos(yt))/(√t)) dt and g(x,y) =∫_0 ^∞ ((e^(−xt) sin(yt))/(√t)) dt with x>0 and y>0 2) find the values of ∫_0 ^∞ ((e^(−2t) cos(t))/(√t)) dt and ∫_0 ^∞ ((e^(−t) cos(2t))/(√t)) dt

$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{xt}} {cos}\left({yt}\right)}{\sqrt{{t}}}\:{dt}\:{and}\:{g}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{xt}} {sin}\left({yt}\right)}{\sqrt{{t}}}\:{dt} \\ $$ $${with}\:{x}>\mathrm{0}\:\:{and}\:{y}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right)\:{find}\:{the}\:{values}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−\mathrm{2}{t}} \:{cos}\left({t}\right)}{\sqrt{{t}}}\:{dt}\:{and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{t}} {cos}\left(\mathrm{2}{t}\right)}{\sqrt{{t}}}\:{dt} \\ $$

Commented bymaxmathsup by imad last updated on 20/Jun/19

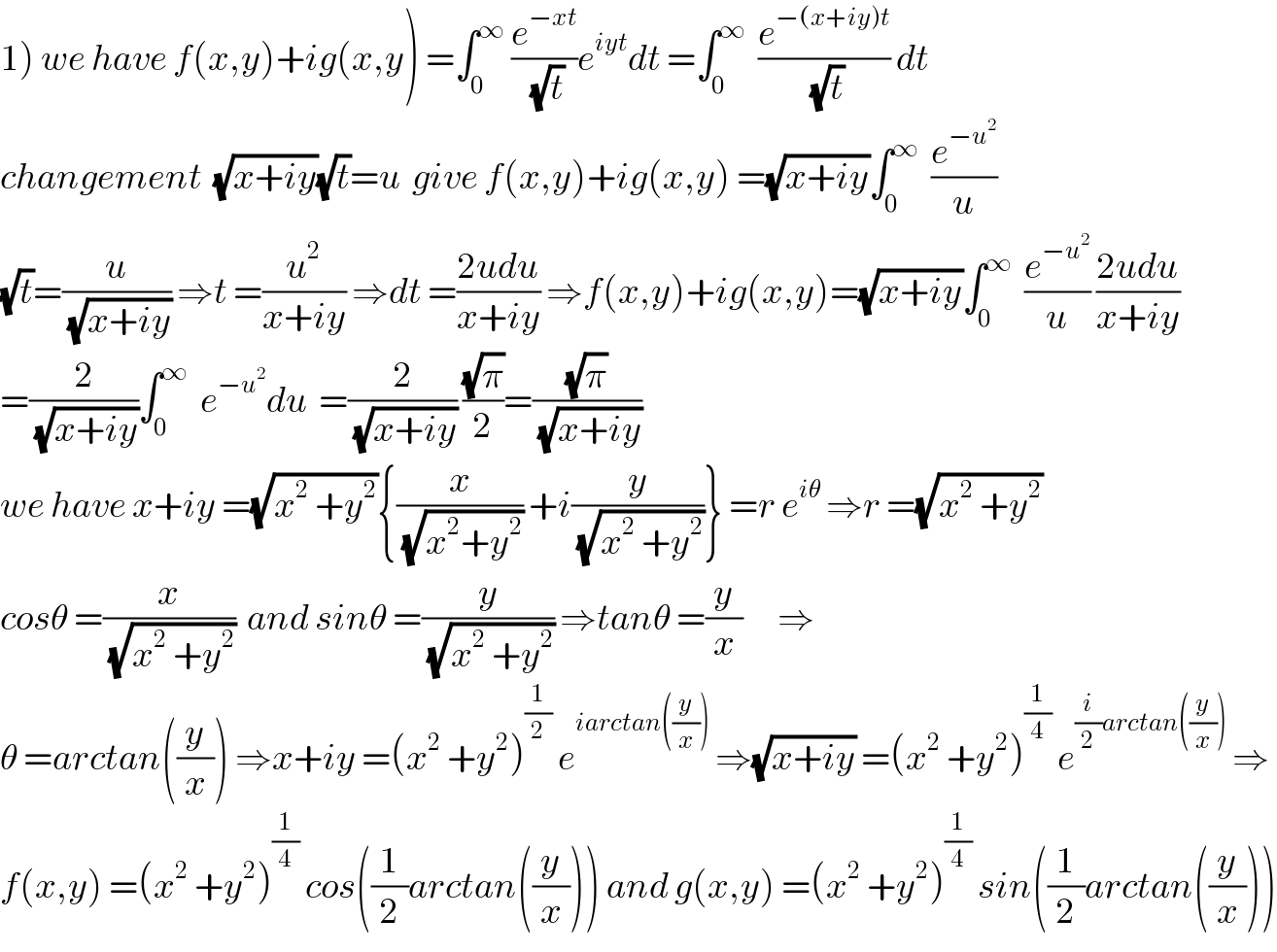
1) we have f(x,y)+ig(x,y) =∫_0 ^∞ (e^(−xt) /(√t))e^(iyt) dt =∫_0 ^∞ (e^(−(x+iy)t) /(√t)) dt changement (√(x+iy))(√t)=u give f(x,y)+ig(x,y) =(√(x+iy))∫_0 ^∞ (e^(−u^2 ) /u) (√t)=(u/(√(x+iy))) ⇒t =(u^2 /(x+iy)) ⇒dt =((2udu)/(x+iy)) ⇒f(x,y)+ig(x,y)=(√(x+iy))∫_0 ^∞ (e^(−u^2 ) /u) ((2udu)/(x+iy)) =(2/(√(x+iy)))∫_0 ^∞ e^(−u^2 ) du =(2/(√(x+iy))) ((√π)/2)=((√π)/(√(x+iy))) we have x+iy =(√(x^2 +y^2 )){(x/(√(x^2 +y^2 ))) +i(y/(√(x^2 +y^2 )))} =r e^(iθ) ⇒r =(√(x^2 +y^2 )) cosθ =(x/(√(x^2 +y^2 ))) and sinθ =(y/(√(x^2 +y^2 ))) ⇒tanθ =(y/x) ⇒ θ =arctan((y/x)) ⇒x+iy =(x^2 +y^2 )^(1/2) e^(iarctan((y/x))) ⇒(√(x+iy)) =(x^2 +y^2 )^(1/4) e^((i/2)arctan((y/x))) ⇒ f(x,y) =(x^2 +y^2 )^(1/4) cos((1/2)arctan((y/x))) and g(x,y) =(x^2 +y^2 )^(1/4) sin((1/2)arctan((y/x)))

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x},{y}\right)+{ig}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{xt}} }{\sqrt{{t}}}{e}^{{iyt}} {dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left({x}+{iy}\right){t}} }{\sqrt{{t}}}\:{dt}\: \\ $$ $${changement}\:\:\sqrt{{x}+{iy}}\sqrt{{t}}={u}\:\:{give}\:{f}\left({x},{y}\right)+{ig}\left({x},{y}\right)\:=\sqrt{{x}+{iy}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{u}^{\mathrm{2}} } }{{u}} \\ $$ $$\sqrt{{t}}=\frac{{u}}{\sqrt{{x}+{iy}}}\:\Rightarrow{t}\:=\frac{{u}^{\mathrm{2}} }{{x}+{iy}}\:\Rightarrow{dt}\:=\frac{\mathrm{2}{udu}}{{x}+{iy}}\:\Rightarrow{f}\left({x},{y}\right)+{ig}\left({x},{y}\right)=\sqrt{{x}+{iy}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{u}^{\mathrm{2}} } }{{u}}\:\frac{\mathrm{2}{udu}}{{x}+{iy}} \\ $$ $$=\frac{\mathrm{2}}{\sqrt{{x}+{iy}}}\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\:\:=\frac{\mathrm{2}}{\sqrt{{x}+{iy}}}\:\frac{\sqrt{\pi}}{\mathrm{2}}=\frac{\sqrt{\pi}}{\sqrt{{x}+{iy}}} \\ $$ $${we}\:{have}\:{x}+{iy}\:=\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\left\{\frac{{x}}{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:+{i}\frac{{y}}{\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}\right\}\:={r}\:{e}^{{i}\theta} \:\Rightarrow{r}\:=\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} } \\ $$ $${cos}\theta\:=\frac{{x}}{\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}\:\:{and}\:{sin}\theta\:=\frac{{y}}{\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}\:\Rightarrow{tan}\theta\:=\frac{{y}}{{x}}\:\:\:\:\:\:\Rightarrow \\ $$ $$\theta\:={arctan}\left(\frac{{y}}{{x}}\right)\:\Rightarrow{x}+{iy}\:=\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{e}^{{iarctan}\left(\frac{{y}}{{x}}\right)} \:\Rightarrow\sqrt{{x}+{iy}}\:=\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{{y}}{{x}}\right)} \:\Rightarrow \\ $$ $${f}\left({x},{y}\right)\:=\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{{y}}{{x}}\right)\right)\:{and}\:{g}\left({x},{y}\right)\:=\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{{y}}{{x}}\right)\right) \\ $$

Commented bymaxmathsup by imad last updated on 20/Jun/19

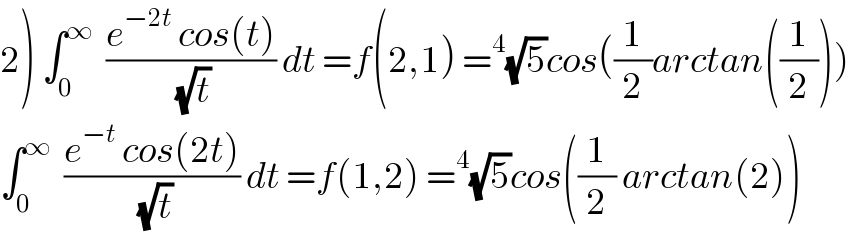
2) ∫_0 ^∞ ((e^(−2t) cos(t))/(√t)) dt =f(2,1) =^4 (√5)cos((1/2)arctan((1/2))) ∫_0 ^∞ ((e^(−t) cos(2t))/(√t)) dt =f(1,2) =^4 (√5)cos((1/2) arctan(2))

$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\mathrm{2}{t}} \:{cos}\left({t}\right)}{\sqrt{{t}}}\:{dt}\:={f}\left(\mathrm{2},\mathrm{1}\right)\:=^{\mathrm{4}} \sqrt{\mathrm{5}}{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} \:{cos}\left(\mathrm{2}{t}\right)}{\sqrt{{t}}}\:{dt}\:={f}\left(\mathrm{1},\mathrm{2}\right)\:=^{\mathrm{4}} \sqrt{\mathrm{5}}{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\mathrm{2}\right)\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com