Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 63190 by Tawa1 last updated on 30/Jun/19

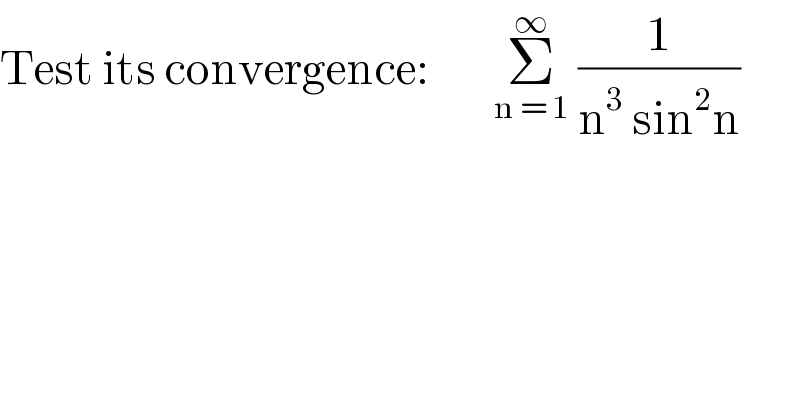
Test its convergence: Σ_(n = 1) ^∞ (1/(n^3 sin^2 n))

$$\mathrm{Test}\:\mathrm{its}\:\mathrm{convergence}:\:\:\:\:\:\:\:\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{n}} \\ $$

Commented by mathmax by abdo last updated on 01/Jul/19

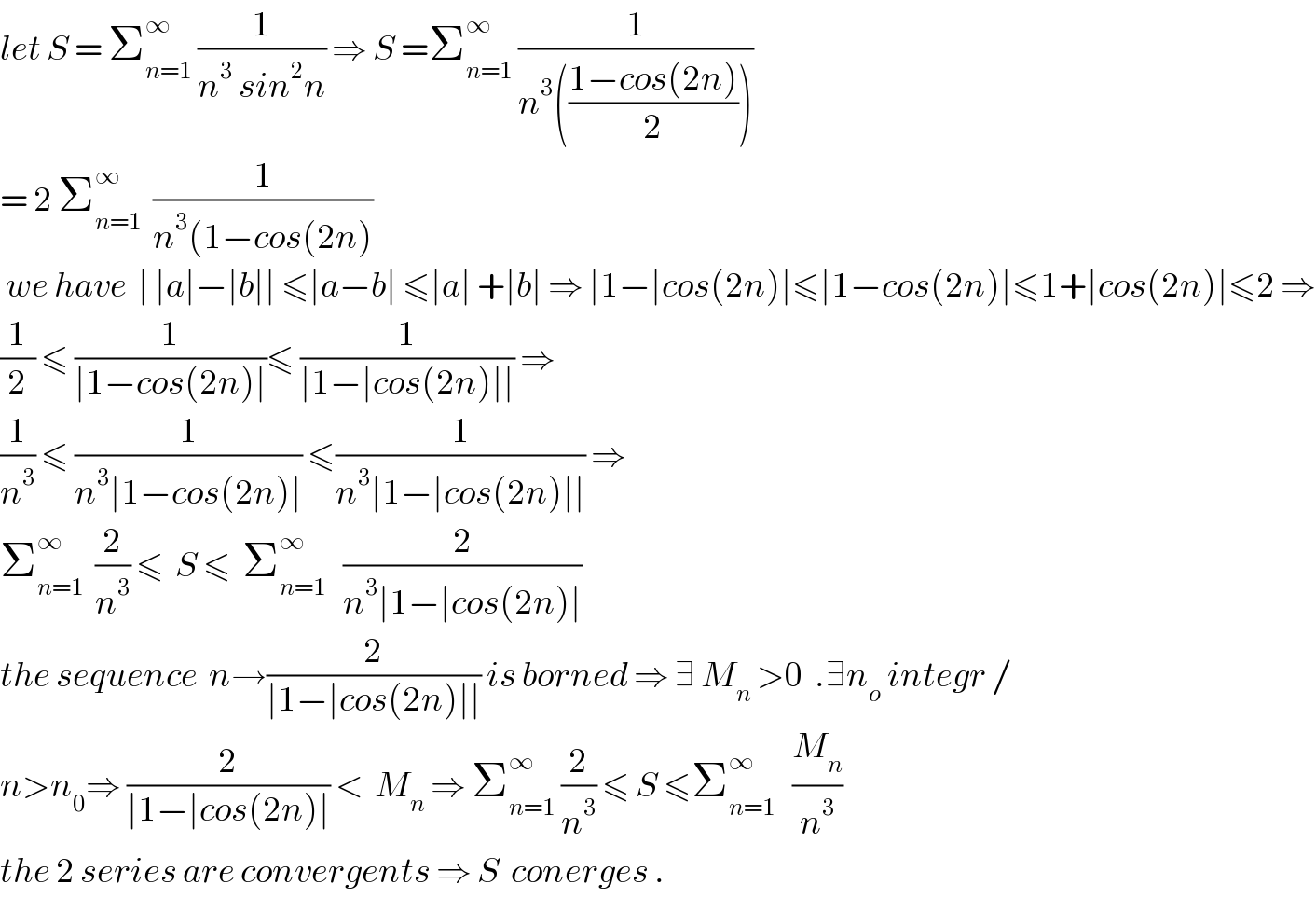
let S = Σ_(n=1) ^∞ (1/(n^3 sin^2 n)) ⇒ S =Σ_(n=1) ^∞ (1/(n^3 (((1−cos(2n))/2)))) = 2 Σ_(n=1) ^∞ (1/(n^3 (1−cos(2n))) we have ∣ ∣a∣−∣b∣∣ ≤∣a−b∣ ≤∣a∣ +∣b∣ ⇒ ∣1−∣cos(2n)∣≤∣1−cos(2n)∣≤1+∣cos(2n)∣≤2 ⇒ (1/2) ≤ (1/(∣1−cos(2n)∣))≤ (1/(∣1−∣cos(2n)∣∣)) ⇒ (1/n^3 ) ≤ (1/(n^3 ∣1−cos(2n)∣)) ≤(1/(n^3 ∣1−∣cos(2n)∣∣)) ⇒ Σ_(n=1) ^∞ (2/n^3 ) ≤ S ≤ Σ_(n=1) ^∞ (2/(n^3 ∣1−∣cos(2n)∣)) the sequence n→(2/(∣1−∣cos(2n)∣∣)) is borned ⇒ ∃ M_n >0 .∃n_o integr / n>n_0 ⇒ (2/(∣1−∣cos(2n)∣)) < M_n ⇒ Σ_(n=1) ^∞ (2/n^3 ) ≤ S ≤Σ_(n=1) ^∞ (M_n /n^3 ) the 2 series are convergents ⇒ S conerges .

$${let}\:{S}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} \:{sin}^{\mathrm{2}} {n}}\:\Rightarrow\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} \left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{n}\right)}{\mathrm{2}}\right)} \\ $$$$=\:\mathrm{2}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} \left(\mathrm{1}−{cos}\left(\mathrm{2}{n}\right)\right.} \\ $$$$\:{we}\:{have}\:\:\mid\:\mid{a}\mid−\mid{b}\mid\mid\:\leqslant\mid{a}−{b}\mid\:\leqslant\mid{a}\mid\:+\mid{b}\mid\:\Rightarrow\:\mid\mathrm{1}−\mid{cos}\left(\mathrm{2}{n}\right)\mid\leqslant\mid\mathrm{1}−{cos}\left(\mathrm{2}{n}\right)\mid\leqslant\mathrm{1}+\mid{cos}\left(\mathrm{2}{n}\right)\mid\leqslant\mathrm{2}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\leqslant\:\frac{\mathrm{1}}{\mid\mathrm{1}−{cos}\left(\mathrm{2}{n}\right)\mid}\leqslant\:\frac{\mathrm{1}}{\mid\mathrm{1}−\mid{cos}\left(\mathrm{2}{n}\right)\mid\mid}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\leqslant\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} \mid\mathrm{1}−{cos}\left(\mathrm{2}{n}\right)\mid}\:\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{3}} \mid\mathrm{1}−\mid{cos}\left(\mathrm{2}{n}\right)\mid\mid}\:\Rightarrow\: \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\:\leqslant\:\:{S}\:\leqslant\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{2}}{{n}^{\mathrm{3}} \mid\mathrm{1}−\mid{cos}\left(\mathrm{2}{n}\right)\mid} \\ $$$${the}\:{sequence}\:\:{n}\rightarrow\frac{\mathrm{2}}{\mid\mathrm{1}−\mid{cos}\left(\mathrm{2}{n}\right)\mid\mid}\:{is}\:{borned}\:\Rightarrow\:\exists\:{M}_{{n}} \:>\mathrm{0}\:\:.\exists{n}_{{o}} \:{integr}\:/ \\ $$$${n}>{n}_{\mathrm{0}} \Rightarrow\:\frac{\mathrm{2}}{\mid\mathrm{1}−\mid{cos}\left(\mathrm{2}{n}\right)\mid}\:<\:\:{M}_{{n}} \:\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\:\leqslant\:{S}\:\leqslant\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{M}_{{n}} }{{n}^{\mathrm{3}} } \\ $$$${the}\:\mathrm{2}\:{series}\:{are}\:{convergents}\:\Rightarrow\:{S}\:\:{conerges}\:. \\ $$

Commented by Tawa1 last updated on 01/Jul/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mathmax by abdo last updated on 01/Jul/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com