
Question Number 63214 by mathmax by abdo last updated on 30/Jun/19
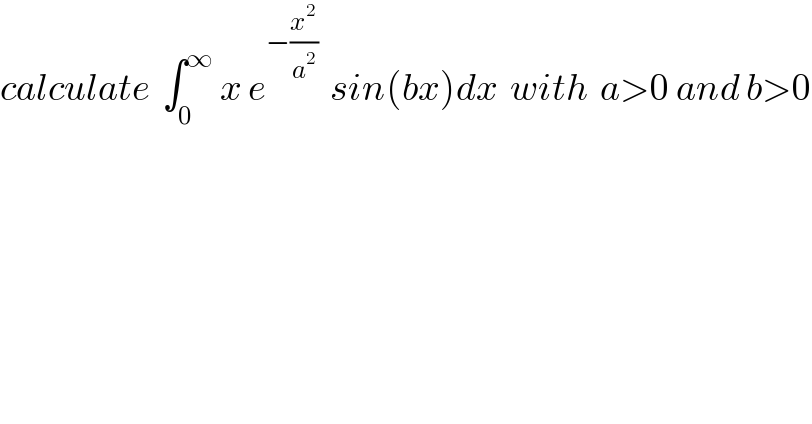
$${calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:\:{sin}\left({bx}\right){dx}\:\:{with}\:\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$
Commented bymathmax by abdo last updated on 01/Jul/19
![let I =∫_0 ^∞ x e^(−(x^2 /a^2 )) s in(bx)dx ⇒ 2I =∫_(−∞) ^(+∞) x e^(−(x^2 /a^2 )) sin(bx)dx by parts u^′ =x e^(−(x^2 /a^2 )) and v =sin(bx) ⇒ 2I =[−(a^2 /2) e^(−(x^2 /a^2 )) sin(bx)]_(−∞) ^(+∞) −∫_(−∞) ^(+∞) −(a^2 /2) e^(−(x^2 /a^2 )) b cos(bx) dx =((a^2 b)/2) ∫_(−∞) ^(+∞) e^(−(x^2 /a^2 )) cos(bx)dx let determine A_λ =∫_(−∞) ^(+∞) e^(−λx^2 ) cos(bx)dx with λ>0 A_λ =Re (∫_(−∞) ^(+∞) e^(−λx^2 +ibx) dx) ∫_(−∞) ^(+∞) e^(−λx^2 +ibx) dx =∫_(−∞) ^(+∞) e^(−{ ((√λ)x)^2 −2(√λ)x((ib)/(2(√λ))) −(b^2 /(4λ)) +(b^2 /(4λ))}) dx =∫_(−∞) ^(+∞) e^(−( (√λ)x +((ib)/(2(√λ))))^2 ) e^(−(b^2 /(4λ))) dx =_((√λ)x +((ib)/(2(√υ)))=u) e^(−(b^2 /(4λ))) ∫_(−∞) ^(+∞) e^(−u^2 ) (du/(√λ)) =((√π)/(√λ)) ⇒ A_λ =((√π)/(√λ)) e^(−(b^2 /(4λ))) ⇒ 2I =((a^2 b)/2) ((√π)/(√λ)) e^(−(b^2 /(4λ))) and λ =(1/a^2 ) ⇒ I =((a^2 b)/4) ((√π)/(1/a)) e^(−(b^2 /(4(1/a^2 )))) =((√π)/4) a^3 b e^(−((a^2 b^2 )/4))](Q63259.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:{s}\:{in}\left({bx}\right){dx}\:\Rightarrow\:\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:{x}\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:{sin}\left({bx}\right){dx}\:\:{by}\:{parts} \\ $$ $${u}^{'} \:={x}\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:\:\:{and}\:{v}\:={sin}\left({bx}\right)\:\Rightarrow \\ $$ $$\mathrm{2}{I}\:=\left[−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:{sin}\left({bx}\right)\right]_{−\infty} ^{+\infty} \:−\int_{−\infty} ^{+\infty} \:\:−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:{b}\:{cos}\left({bx}\right)\:{dx} \\ $$ $$=\frac{{a}^{\mathrm{2}} {b}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:{cos}\left({bx}\right){dx}\:\:\:{let}\:{determine}\:{A}_{\lambda} =\int_{−\infty} ^{+\infty} \:{e}^{−\lambda{x}^{\mathrm{2}} } {cos}\left({bx}\right){dx}\:{with}\:\lambda>\mathrm{0} \\ $$ $${A}_{\lambda} ={Re}\:\left(\int_{−\infty} ^{+\infty} \:{e}^{−\lambda{x}^{\mathrm{2}} +{ibx}} {dx}\right) \\ $$ $$\int_{−\infty} ^{+\infty} \:\:{e}^{−\lambda{x}^{\mathrm{2}} \:+{ibx}} {dx}\:=\int_{−\infty} ^{+\infty} \:\:{e}^{−\left\{\:\left(\sqrt{\lambda}{x}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\lambda}{x}\frac{{ib}}{\mathrm{2}\sqrt{\lambda}}\:\:−\frac{{b}^{\mathrm{2}} }{\mathrm{4}\lambda}\:+\frac{{b}^{\mathrm{2}} }{\mathrm{4}\lambda}\right\}} {dx} \\ $$ $$=\int_{−\infty} ^{+\infty} \:\:{e}^{−\left(\:\sqrt{\lambda}{x}\:+\frac{{ib}}{\mathrm{2}\sqrt{\lambda}}\right)^{\mathrm{2}} } \:{e}^{−\frac{{b}^{\mathrm{2}} }{\mathrm{4}\lambda}} \:{dx}\:=_{\sqrt{\lambda}{x}\:+\frac{{ib}}{\mathrm{2}\sqrt{\upsilon}}={u}} \:\:\:\:\:{e}^{−\frac{{b}^{\mathrm{2}} }{\mathrm{4}\lambda}} \int_{−\infty} ^{+\infty} \:{e}^{−{u}^{\mathrm{2}} } \frac{{du}}{\sqrt{\lambda}}\:=\frac{\sqrt{\pi}}{\sqrt{\lambda}}\:\Rightarrow\:{A}_{\lambda} =\frac{\sqrt{\pi}}{\sqrt{\lambda}}\:{e}^{−\frac{{b}^{\mathrm{2}} }{\mathrm{4}\lambda}} \:\Rightarrow \\ $$ $$\mathrm{2}{I}\:=\frac{{a}^{\mathrm{2}} {b}}{\mathrm{2}}\:\frac{\sqrt{\pi}}{\sqrt{\lambda}}\:{e}^{−\frac{{b}^{\mathrm{2}} }{\mathrm{4}\lambda}} \:\:\:\:\:\:\:\:{and}\:\lambda\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\Rightarrow \\ $$ $${I}\:=\frac{{a}^{\mathrm{2}} {b}}{\mathrm{4}}\:\frac{\sqrt{\pi}}{\frac{\mathrm{1}}{{a}}}\:{e}^{−\frac{{b}^{\mathrm{2}} }{\mathrm{4}\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}} =\frac{\sqrt{\pi}}{\mathrm{4}}\:{a}^{\mathrm{3}} {b}\:{e}^{−\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{4}}} \\ $$ $$ \\ $$
