Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 63427 by Rio Michael last updated on 04/Jul/19

(1) A plane contains the lines ((x+1)/2)=((4−y)/2)=((z−2)/3) and r= (2i+2j + 12k)+t(−i+2j +4k). find (a) the angle between these lines. (b) A cartesian equation of the plane. (2) Given the lines l_1 :((x−10)/3)=((y−1)/1)=((z−9)/4) l_2 :r=(−9j+13k)+μ(i+2j−3k) where μ is a parameter; l_3 :((x+10)/4)=((y+5)/3)=((z+4)/1). a) show that the point (4,−1,1) is common to l_1 and l_2 . Find b) the point of intersection of l_2 and l_3 . c) A vector parametric equation of the plane containing the lines l_2 and l_3 . sir Forkum Michael

$$\left(\mathrm{1}\right)\:{A}\:{plane}\:{contains}\:{the}\:{lines}\:\frac{{x}+\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{4}−{y}}{\mathrm{2}}=\frac{{z}−\mathrm{2}}{\mathrm{3}}\:{and}\: \\ $$$${r}=\:\left(\mathrm{2}{i}+\mathrm{2}{j}\:+\:\mathrm{12}{k}\right)+{t}\left(−{i}+\mathrm{2}{j}\:+\mathrm{4}{k}\right).\:{find} \\ $$$$\left({a}\right)\:{the}\:{angle}\:{between}\:{these}\:{lines}. \\ $$$$\left({b}\right)\:{A}\:{cartesian}\:{equation}\:{of}\:{the}\:{plane}. \\ $$$$\left(\mathrm{2}\right)\:{Given}\:{the}\:{lines}\:\boldsymbol{{l}}_{\mathrm{1}} :\frac{{x}−\mathrm{10}}{\mathrm{3}}=\frac{{y}−\mathrm{1}}{\mathrm{1}}=\frac{{z}−\mathrm{9}}{\mathrm{4}}\:\:\boldsymbol{{l}}_{\mathrm{2}} :{r}=\left(−\mathrm{9}{j}+\mathrm{13}{k}\right)+\mu\left({i}+\mathrm{2}{j}−\mathrm{3}{k}\right) \\ $$$${where}\:\mu\:{is}\:{a}\:{parameter};\:\boldsymbol{{l}}_{\mathrm{3}} :\frac{{x}+\mathrm{10}}{\mathrm{4}}=\frac{{y}+\mathrm{5}}{\mathrm{3}}=\frac{{z}+\mathrm{4}}{\mathrm{1}}. \\ $$$$\left.{a}\right)\:{show}\:{that}\:{the}\:{point}\:\left(\mathrm{4},−\mathrm{1},\mathrm{1}\right)\:{is}\:{common}\:{to}\:\boldsymbol{{l}}_{\mathrm{1}} \:{and}\:\boldsymbol{{l}}_{\mathrm{2}} .\:{Find} \\ $$$$\left.{b}\right)\:{the}\:{point}\:{of}\:{intersection}\:{of}\:\boldsymbol{{l}}_{\mathrm{2}} \:{and}\:\boldsymbol{{l}}_{\mathrm{3}} . \\ $$$$\left.{c}\right)\:{A}\:{vector}\:{parametric}\:{equation}\:{of}\:{the}\:{plane}\:{containing}\:{the} \\ $$$${lines}\:\boldsymbol{{l}}_{\mathrm{2}} \:{and}\:\boldsymbol{{l}}_{\mathrm{3}} . \\ $$$${sir}\:{Forkum}\:{Michael} \\ $$

Commented by Tony Lin last updated on 04/Jul/19

(2)(b) let { ((l_2 :(x/1)=((y+9)/2)=((z−13)/(−3))=μ)),((l_3 :((x+10)/4)=((y+5)/3)=((z+4)/1)=s)) :} ⇒μ=−10+4s −9+2μ=−5+3s 13−3μ=−4+s ⇒no solution to the eqations ⇒l_2 &l_3 are skew lines ⇒there is no point of intersection of l_(2 ) & l_3 (2)(c) ∵l_2 & l_3 are skew lines ∴there is no plane containing the lines

$$\left(\mathrm{2}\right)\left({b}\right) \\ $$$${let\begin{cases}{\boldsymbol{{l}}_{\mathrm{2}} :\frac{{x}}{\mathrm{1}}=\frac{{y}+\mathrm{9}}{\mathrm{2}}=\frac{{z}−\mathrm{13}}{−\mathrm{3}}=\mu}\\{\boldsymbol{{l}}_{\mathrm{3}} :\frac{{x}+\mathrm{10}}{\mathrm{4}}=\frac{{y}+\mathrm{5}}{\mathrm{3}}=\frac{{z}+\mathrm{4}}{\mathrm{1}}={s}}\end{cases}} \\ $$$$\Rightarrow\mu=−\mathrm{10}+\mathrm{4}{s} \\ $$$$\:\:\:\:\:−\mathrm{9}+\mathrm{2}\mu=−\mathrm{5}+\mathrm{3}{s} \\ $$$$\:\:\:\:\:\mathrm{13}−\mathrm{3}\mu=−\mathrm{4}+{s} \\ $$$$\Rightarrow{no}\:{solution}\:{to}\:{the}\:{eqations} \\ $$$$\Rightarrow\boldsymbol{{l}}_{\mathrm{2}} \:\&\boldsymbol{{l}}_{\mathrm{3}} \:{are}\:{skew}\:{lines} \\ $$$$\Rightarrow{there}\:{is}\:{no}\:{point}\:{of}\:{intersection}\:{of}\:\boldsymbol{{l}}_{\mathrm{2}\:} \&\:\boldsymbol{{l}}_{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\left({c}\right) \\ $$$$\because\boldsymbol{{l}}_{\mathrm{2}} \&\:\boldsymbol{{l}}_{\mathrm{3}} \:{are}\:{skew}\:{lines} \\ $$$$\therefore{there}\:{is}\:{no}\:{plane}\:{containing}\:{the}\:{lines} \\ $$

Commented by Tony Lin last updated on 04/Jul/19

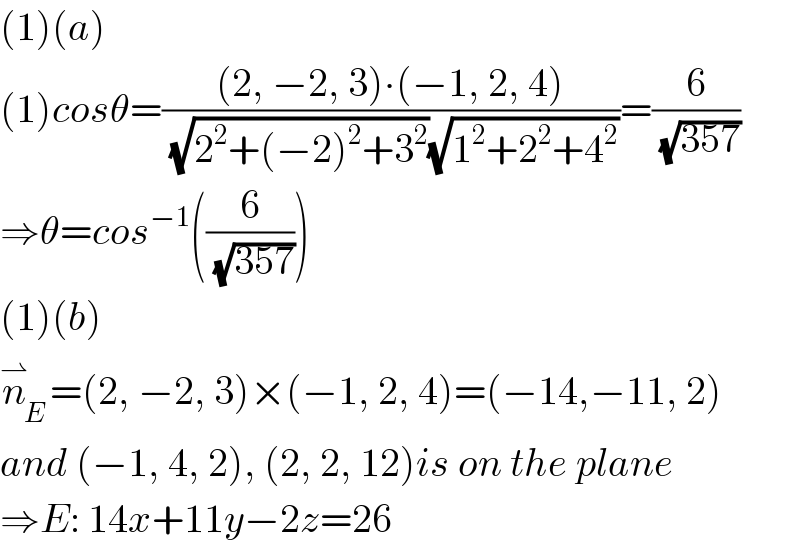
(1)(a) (1)cosθ=(((2, −2, 3)∙(−1, 2, 4))/((√(2^2 +(−2)^2 +3^2 ))(√(1^2 +2^2 +4^2 ))))=(6/(√(357))) ⇒θ=cos^(−1) ((6/(√(357)))) (1)(b) n_E ^⇀ =(2, −2, 3)×(−1, 2, 4)=(−14,−11, 2) and (−1, 4, 2), (2, 2, 12)is on the plane ⇒E: 14x+11y−2z=26

$$\left(\mathrm{1}\right)\left({a}\right) \\ $$$$\left(\mathrm{1}\right){cos}\theta=\frac{\left(\mathrm{2},\:−\mathrm{2},\:\mathrm{3}\right)\centerdot\left(−\mathrm{1},\:\mathrm{2},\:\mathrm{4}\right)}{\sqrt{\mathrm{2}^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }}=\frac{\mathrm{6}}{\sqrt{\mathrm{357}}} \\ $$$$\Rightarrow\theta={cos}^{−\mathrm{1}} \left(\frac{\mathrm{6}}{\sqrt{\mathrm{357}}}\right) \\ $$$$\left(\mathrm{1}\right)\left({b}\right) \\ $$$$\overset{\rightharpoonup} {{n}}_{{E}} =\left(\mathrm{2},\:−\mathrm{2},\:\mathrm{3}\right)×\left(−\mathrm{1},\:\mathrm{2},\:\mathrm{4}\right)=\left(−\mathrm{14},−\mathrm{11},\:\mathrm{2}\right) \\ $$$${and}\:\left(−\mathrm{1},\:\mathrm{4},\:\mathrm{2}\right),\:\left(\mathrm{2},\:\mathrm{2},\:\mathrm{12}\right){is}\:{on}\:{the}\:{plane} \\ $$$$\Rightarrow{E}:\:\mathrm{14}{x}+\mathrm{11}{y}−\mathrm{2}{z}=\mathrm{26} \\ $$

Commented by Tony Lin last updated on 04/Jul/19

(2)(a) let { ((l_1 :((x−10)/3)=((y−1)/1)=((z−9)/4)=t)),((l_2 :(x/1)=((y+9)/2)=((z−13)/(−3))=μ)) :} ⇒10+3t=μ 1+t=−9+2μ 9+4t=13−3μ ⇒t=−2, μ=4 ⇒(4, −1, −1) is the point of intersection of l_1 &l_2

$$\left(\mathrm{2}\right)\left({a}\right) \\ $$$${let}\:\begin{cases}{\boldsymbol{{l}}_{\mathrm{1}} :\frac{{x}−\mathrm{10}}{\mathrm{3}}=\frac{{y}−\mathrm{1}}{\mathrm{1}}=\frac{{z}−\mathrm{9}}{\mathrm{4}}={t}}\\{\boldsymbol{{l}}_{\mathrm{2}} :\frac{{x}}{\mathrm{1}}=\frac{{y}+\mathrm{9}}{\mathrm{2}}=\frac{{z}−\mathrm{13}}{−\mathrm{3}}=\mu}\end{cases} \\ $$$$\Rightarrow\mathrm{10}+\mathrm{3}{t}=\mu \\ $$$$\:\:\:\:\:\mathrm{1}+{t}=−\mathrm{9}+\mathrm{2}\mu \\ $$$$\:\:\:\:\:\mathrm{9}+\mathrm{4}{t}=\mathrm{13}−\mathrm{3}\mu \\ $$$$\Rightarrow{t}=−\mathrm{2},\:\mu=\mathrm{4} \\ $$$$\Rightarrow\left(\mathrm{4},\:−\mathrm{1},\:−\mathrm{1}\right) \\ $$$$\:\:\:\:\:{is}\:{the}\:{point}\:{of}\:{intersection}\:{of}\:\boldsymbol{{l}}_{\mathrm{1}} \&\boldsymbol{{l}}_{\mathrm{2}} \\ $$

Commented by Rio Michael last updated on 04/Jul/19

perfect.

$${perfect}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com