Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 63922 by raj last updated on 11/Jul/19

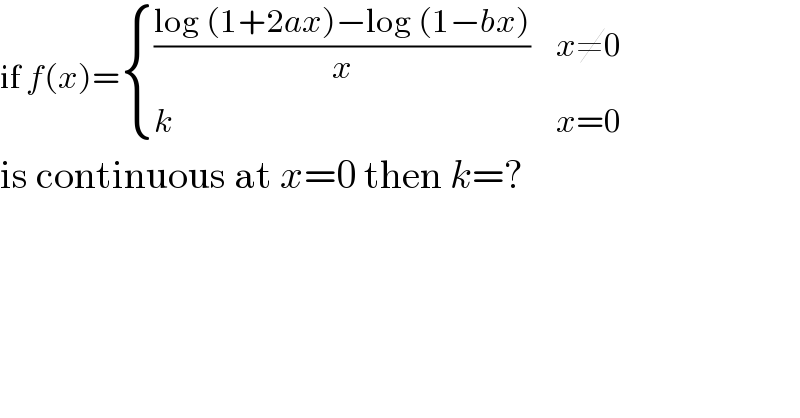
if f(x)= { (((log (1+2ax)−log (1−bx))/x),(x≠0)),(k,(x=0)) :} is continuous at x=0 then k=?

$$\mathrm{if}\:{f}\left({x}\right)=\begin{cases}{\frac{\mathrm{log}\:\left(\mathrm{1}+\mathrm{2}{ax}\right)−\mathrm{log}\:\left(\mathrm{1}−{bx}\right)}{{x}}}&{{x}\neq\mathrm{0}}\\{{k}}&{{x}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{is}\:\mathrm{continuous}\:\mathrm{at}\:{x}=\mathrm{0}\:\mathrm{then}\:{k}=? \\ $$

Commented by kaivan.ahmadi last updated on 11/Jul/19

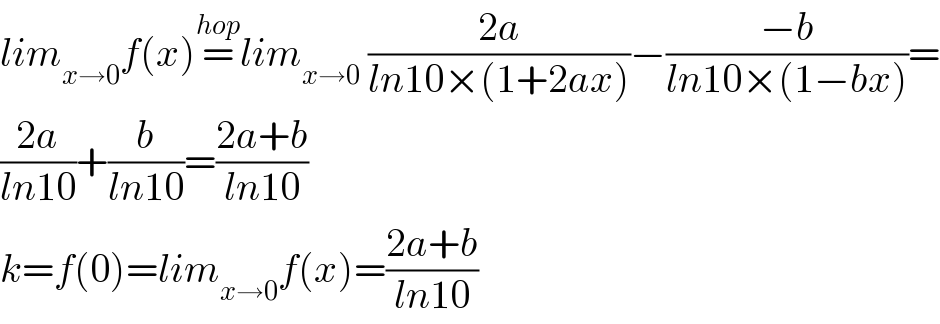
lim_(x→0) f(x)=^(hop) lim_(x→0 ) ((2a)/(ln10×(1+2ax)))−((−b)/(ln10×(1−bx)))= ((2a)/(ln10))+(b/(ln10))=((2a+b)/(ln10)) k=f(0)=lim_(x→0) f(x)=((2a+b)/(ln10))

$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)\overset{{hop}} {=}{lim}_{{x}\rightarrow\mathrm{0}\:\:} \frac{\mathrm{2}{a}}{{ln}\mathrm{10}×\left(\mathrm{1}+\mathrm{2}{ax}\right)}−\frac{−{b}}{{ln}\mathrm{10}×\left(\mathrm{1}−{bx}\right)}= \\ $$$$\frac{\mathrm{2}{a}}{{ln}\mathrm{10}}+\frac{{b}}{{ln}\mathrm{10}}=\frac{\mathrm{2}{a}+{b}}{{ln}\mathrm{10}} \\ $$$${k}={f}\left(\mathrm{0}\right)={lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\frac{\mathrm{2}{a}+{b}}{{ln}\mathrm{10}} \\ $$

Commented by mathmax by abdo last updated on 12/Jul/19

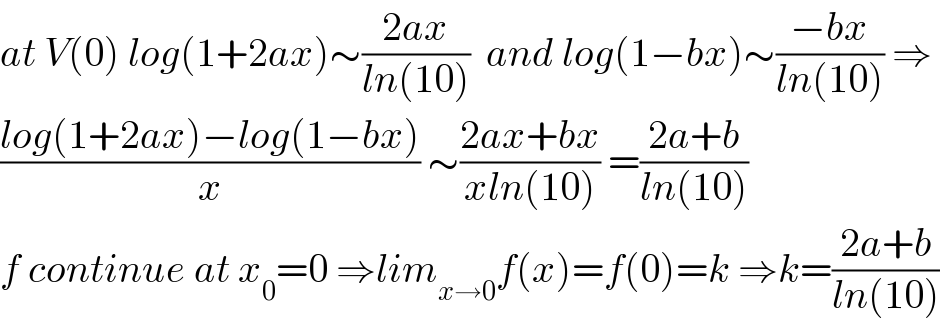
at V(0) log(1+2ax)∼((2ax)/(ln(10))) and log(1−bx)∼((−bx)/(ln(10))) ⇒ ((log(1+2ax)−log(1−bx))/x) ∼((2ax+bx)/(xln(10))) =((2a+b)/(ln(10))) f continue at x_0 =0 ⇒lim_(x→0) f(x)=f(0)=k ⇒k=((2a+b)/(ln(10)))

$${at}\:{V}\left(\mathrm{0}\right)\:{log}\left(\mathrm{1}+\mathrm{2}{ax}\right)\sim\frac{\mathrm{2}{ax}}{{ln}\left(\mathrm{10}\right)}\:\:{and}\:{log}\left(\mathrm{1}−{bx}\right)\sim\frac{−{bx}}{{ln}\left(\mathrm{10}\right)}\:\Rightarrow \\ $$$$\frac{{log}\left(\mathrm{1}+\mathrm{2}{ax}\right)−{log}\left(\mathrm{1}−{bx}\right)}{{x}}\:\sim\frac{\mathrm{2}{ax}+{bx}}{{xln}\left(\mathrm{10}\right)}\:=\frac{\mathrm{2}{a}+{b}}{{ln}\left(\mathrm{10}\right)} \\ $$$${f}\:{continue}\:{at}\:{x}_{\mathrm{0}} =\mathrm{0}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)={f}\left(\mathrm{0}\right)={k}\:\Rightarrow{k}=\frac{\mathrm{2}{a}+{b}}{{ln}\left(\mathrm{10}\right)} \\ $$

Commented by raj last updated on 11/Jul/19

thank you

$${thank}\:{you} \\ $$

Commented by Mikael last updated on 11/Jul/19

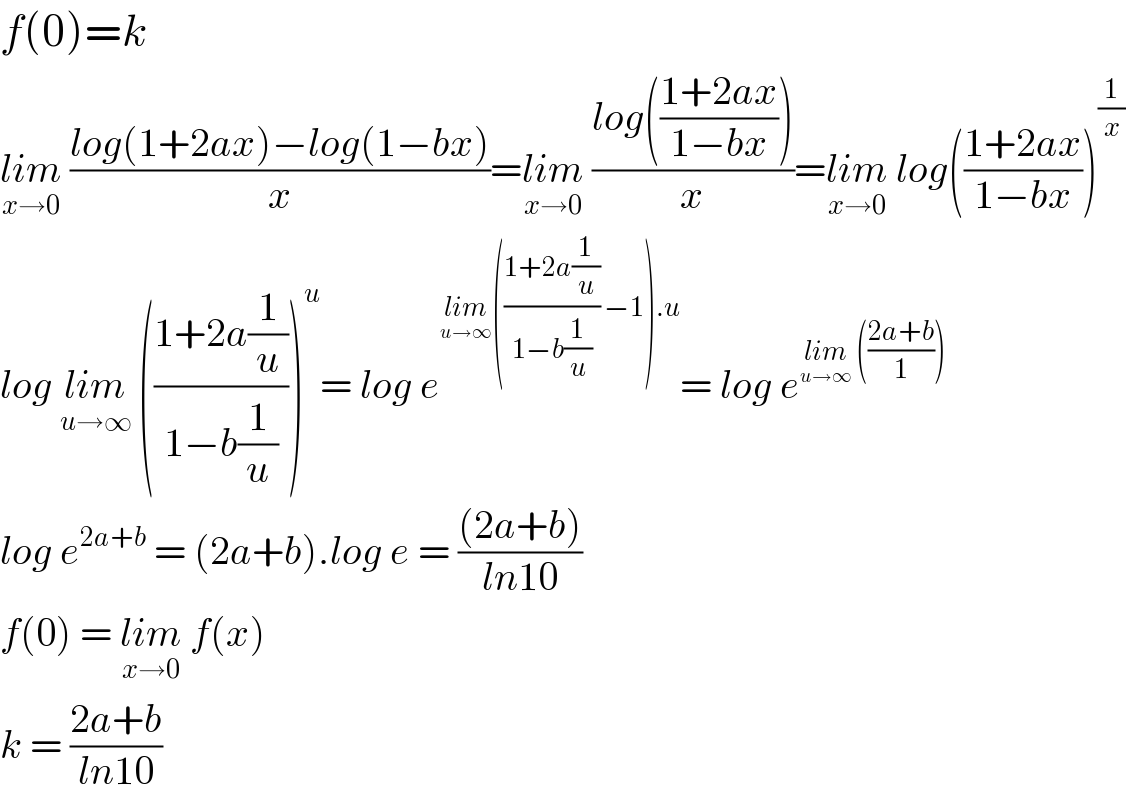
f(0)=k lim_(x→0) ((log(1+2ax)−log(1−bx))/x)=lim_(x→0) ((log(((1+2ax)/(1−bx))))/x)=lim_(x→0) log(((1+2ax)/(1−bx)))^(1/x) log lim_(u→∞) (((1+2a(1/u))/(1−b(1/u))))^u = log e^(lim_(u→∞) (((1+2a(1/u))/(1−b(1/u))) −1).u) = log e^(lim_(u→∞) (((2a+b)/1))) log e^(2a+b) = (2a+b).log e = (((2a+b))/(ln10)) f(0) = lim_(x→0) f(x) k = ((2a+b)/(ln10))

$${f}\left(\mathrm{0}\right)={k} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{log}\left(\mathrm{1}+\mathrm{2}{ax}\right)−{log}\left(\mathrm{1}−{bx}\right)}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{log}\left(\frac{\mathrm{1}+\mathrm{2}{ax}}{\mathrm{1}−{bx}}\right)}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:{log}\left(\frac{\mathrm{1}+\mathrm{2}{ax}}{\mathrm{1}−{bx}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${log}\:\underset{{u}\rightarrow\infty} {{lim}}\:\left(\frac{\mathrm{1}+\mathrm{2}{a}\frac{\mathrm{1}}{{u}}}{\mathrm{1}−{b}\frac{\mathrm{1}}{{u}}}\right)^{{u}} =\:{log}\:{e}^{\underset{{u}\rightarrow\infty} {{lim}}\left(\frac{\mathrm{1}+\mathrm{2}{a}\frac{\mathrm{1}}{{u}}}{\mathrm{1}−{b}\frac{\mathrm{1}}{{u}}}\:−\mathrm{1}\right).{u}} =\:{log}\:{e}^{\underset{{u}\rightarrow\infty} {{lim}}\:\left(\frac{\mathrm{2}{a}+{b}}{\mathrm{1}}\right)} \\ $$$${log}\:{e}^{\mathrm{2}{a}+{b}} \:=\:\left(\mathrm{2}{a}+{b}\right).{log}\:{e}\:=\:\frac{\left(\mathrm{2}{a}+{b}\right)}{{ln}\mathrm{10}} \\ $$$${f}\left(\mathrm{0}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:{f}\left({x}\right) \\ $$$${k}\:=\:\frac{\mathrm{2}{a}+{b}}{{ln}\mathrm{10}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com