Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 64305 by aliesam last updated on 16/Jul/19

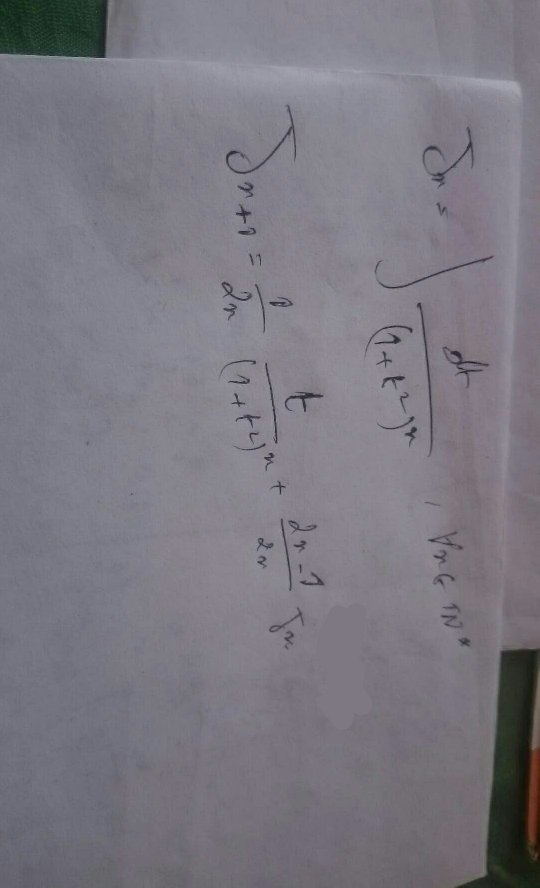
Commented by aliesam last updated on 16/Jul/19

prove that

$${prove}\:{that} \\ $$

Commented by mathmax by abdo last updated on 16/Jul/19

let J_n =∫ (dt/((1+t^2 )^n )) ⇒J_n =∫ ((1+t^2 )/((1+t^2 )^(n+1) ))dt =∫ (dt/((1+t^2 )^(n+1) )) +∫ (t^2 /((1+t^2 )^(n+1) )) dt ∫ (dt/((1+t^2 )^(n+1) )) =J_(n+1) and by parts u =t ant v^′ =t(1+t^2 )^(−n−1) ∫ (t^2 /((1+t^2 )^(n+1) ))dt =t (−(1/(2n))(1+t^2 )^(−n) )−∫ −(1/(2n))(1+t^2 )^(−n) dt =−(1/(2n)) (t/((1+t^2 )^n )) +(1/(2n)) J_n ⇒J_n =J_(n+1) −(1/(2n))(t/((1+t^2 )^n )) +(1/(2n)) J_n ⇒ (1−(1/(2n)))J_n =−(t/(2n(1+t^2 )^n )) +J_(n+1) ⇒ (2n−1)J_n = 2n J_(n+1) −(t/((1+t^2 )^n ))

$${let}\:{J}_{{n}} =\int\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }\:\Rightarrow{J}_{{n}} =\int\:\:\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }{dt} \\ $$$$=\int\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }\:+\int\:\:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }\:{dt}\: \\ $$$$\int\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }\:={J}_{{n}+\mathrm{1}} \:\:\:\:\:{and}\:{by}\:{parts}\:{u}\:={t}\:\:{ant}\:{v}^{'} \:={t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{−{n}−\mathrm{1}} \\ $$$$\int\:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }{dt}\:={t}\:\left(−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{n}}}\left(\mathrm{1}+\boldsymbol{{t}}^{\mathrm{2}} \right)^{−\boldsymbol{{n}}} \right)−\int\:\:\:−\frac{\mathrm{1}}{\mathrm{2}{n}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{−{n}} {dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{n}}\:\:\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }\:\:+\frac{\mathrm{1}}{\mathrm{2}{n}}\:{J}_{{n}} \:\Rightarrow{J}_{{n}} ={J}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}{n}}\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }\:+\frac{\mathrm{1}}{\mathrm{2}{n}}\:{J}_{{n}} \:\Rightarrow \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right){J}_{{n}} =−\frac{{t}}{\mathrm{2}{n}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }\:+{J}_{{n}+\mathrm{1}} \:\Rightarrow \\ $$$$\left(\mathrm{2}{n}−\mathrm{1}\right){J}_{{n}} =\:\mathrm{2}{n}\:{J}_{{n}+\mathrm{1}} −\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} } \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 16/Jul/19

⇒2n J_(n+1) =(2n−1)J_n +(t/((1+t^2 )^n )) ⇒ J_(n+1) =((2n−1)/(2n)) J_n +(t/(2n(1+t^2 )^n ))

$$\Rightarrow\mathrm{2}{n}\:{J}_{{n}+\mathrm{1}} =\left(\mathrm{2}{n}−\mathrm{1}\right){J}_{{n}} \:\:+\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }\:\Rightarrow \\ $$$${J}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}}\:{J}_{{n}} \:\:+\frac{{t}}{\mathrm{2}{n}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} } \\ $$

Commented by aliesam last updated on 16/Jul/19

thank you sir but what about starting from j_n +1 ?

$${thank}\:{you}\:{sir}\: \\ $$$${but}\:{what}\:{about}\:{starting}\:{from}\:{j}_{{n}} +\mathrm{1}\:? \\ $$

Commented by mathmax by abdo last updated on 16/Jul/19

in ordr to appear J_n

$${in}\:{ordr}\:{to}\:{appear}\:{J}_{{n}} \\ $$

Commented by aliesam last updated on 16/Jul/19

yes sir

$${yes}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com