
Question Number 65782 by Rio Michael last updated on 03/Aug/19

$$\:{Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\:\mathrm{4}\right)^{\mathrm{7}} {dx} \\ $$$${hence}\:{show}\:{that}\:\:\frac{{d}}{{dx}}\left({coshx}\right)\:=\:{sinh}\:{x} \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
![we have (3x^2 −2x+4)^7 =Σ_(k=0) ^7 C_7 ^k (3x^2 −2x)^k 4^(7−k) =Σ_(k=0) ^7 x^k C_7 ^k (3x−2)^k 4^(7−k) =Σ_(k=0) ^7 4^(7−k) x^k C_7 ^k { Σ_(p=0) ^k C_k ^p (3x)^p (−2)^(k−p) } =Σ_(k=0) ^7 4^(7−k) C_7 ^k {Σ_(p=0) ^k (−2)^(k−p) 3^p C_k ^p x^(p+k) } ⇒ ∫_0 ^2 (3x^2 −2x +4)^7 dx =[Σ_(k=0) ^7 4^(7−k) C_7 ^k {Σ_(p=0) ^k (−2)^(k−p) 3^p C_k ^p (x^(p+k+1) /(p+k+1))}]_0 ^2 =Σ_(k=0) ^7 4^(7−k) C_7 ^k {Σ_(p=0) ^k (−2)^(k−p) 3^p C_k ^p (2^(p+k+1) /(p+k+1))}](Q65789.png)
$${we}\:{have}\:\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{7}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:{C}_{\mathrm{7}} ^{{k}} \left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{{k}} \:\mathrm{4}^{\mathrm{7}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:{x}^{{k}} \:\:{C}_{\mathrm{7}} ^{{k}} \left(\mathrm{3}{x}−\mathrm{2}\right)^{{k}} \:\mathrm{4}^{\mathrm{7}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:\mathrm{4}^{\mathrm{7}−{k}} \:{x}^{{k}} {C}_{\mathrm{7}} ^{{k}} \left\{\:\sum_{{p}=\mathrm{0}} ^{{k}} \:{C}_{{k}} ^{{p}} \:\left(\mathrm{3}{x}\right)^{{p}} \left(−\mathrm{2}\right)^{{k}−{p}} \right\} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:\mathrm{4}^{\mathrm{7}−{k}} {C}_{\mathrm{7}} ^{{k}} \:\left\{\sum_{{p}=\mathrm{0}} ^{{k}} \left(−\mathrm{2}\right)^{{k}−{p}} \mathrm{3}^{{p}} \:{C}_{{k}} ^{{p}} \:\:{x}^{{p}+{k}} \:\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{4}\right)^{\mathrm{7}} {dx}\:=\left[\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:\mathrm{4}^{\mathrm{7}−{k}} \:{C}_{\mathrm{7}} ^{{k}} \left\{\sum_{{p}=\mathrm{0}} ^{{k}} \left(−\mathrm{2}\right)^{{k}−{p}} \:\mathrm{3}^{{p}} \:{C}_{{k}} ^{{p}} \:\frac{{x}^{{p}+{k}+\mathrm{1}} }{{p}+{k}+\mathrm{1}}\right\}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:\mathrm{4}^{\mathrm{7}−{k}} \:{C}_{\mathrm{7}} ^{{k}} \left\{\sum_{{p}=\mathrm{0}} ^{{k}} \left(−\mathrm{2}\right)^{{k}−{p}} \mathrm{3}^{{p}} \:{C}_{{k}} ^{{p}} \:\frac{\mathrm{2}^{{p}+{k}+\mathrm{1}} }{{p}+{k}+\mathrm{1}}\right\} \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
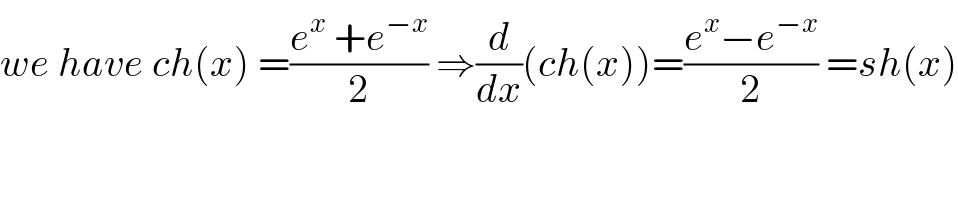
$${we}\:{have}\:{ch}\left({x}\right)\:=\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}\:\Rightarrow\frac{{d}}{{dx}}\left({ch}\left({x}\right)\right)=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}\:={sh}\left({x}\right) \\ $$
Commented by Rio Michael last updated on 04/Aug/19

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
$${you}\:{are}\:{welcome}. \\ $$
