Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 66562 by Rio Michael last updated on 17/Aug/19

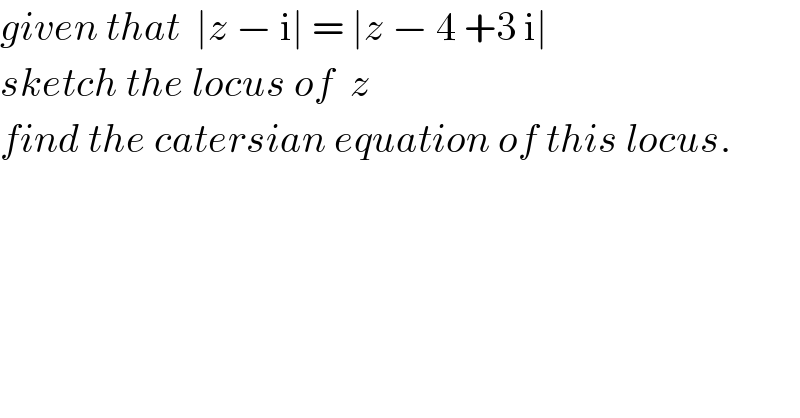
given that ∣z − i∣ = ∣z − 4 +3 i∣ sketch the locus of z find the catersian equation of this locus.

$${given}\:{that}\:\:\mid{z}\:−\:\mathrm{i}\mid\:=\:\mid{z}\:−\:\mathrm{4}\:+\mathrm{3}\:\mathrm{i}\mid \\ $$$${sketch}\:{the}\:{locus}\:{of}\:\:{z} \\ $$$${find}\:{the}\:{catersian}\:{equation}\:{of}\:{this}\:{locus}. \\ $$

Commented by mathmax by abdo last updated on 17/Aug/19

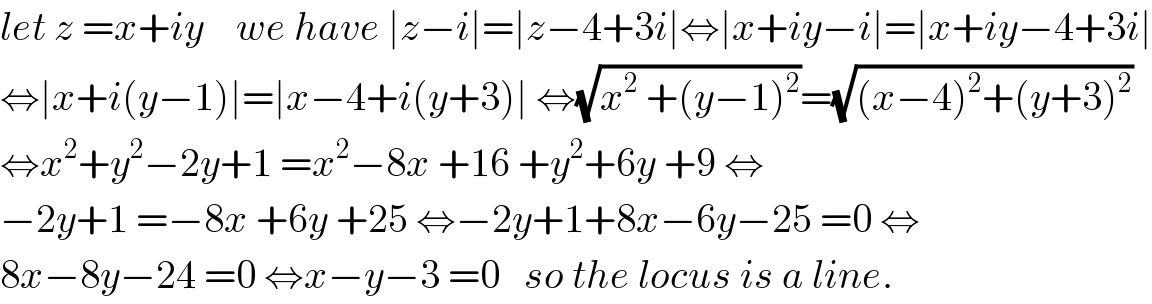
let z =x+iy we have ∣z−i∣=∣z−4+3i∣⇔∣x+iy−i∣=∣x+iy−4+3i∣ ⇔∣x+i(y−1)∣=∣x−4+i(y+3)∣ ⇔(√(x^2 +(y−1)^2 ))=(√((x−4)^2 +(y+3)^2 )) ⇔x^2 +y^2 −2y+1 =x^2 −8x +16 +y^2 +6y +9 ⇔ −2y+1 =−8x +6y +25 ⇔−2y+1+8x−6y−25 =0 ⇔ 8x−8y−24 =0 ⇔x−y−3 =0 so the locus is a line.

$${let}\:{z}\:={x}+{iy}\:\:\:\:{we}\:{have}\:\mid{z}−{i}\mid=\mid{z}−\mathrm{4}+\mathrm{3}{i}\mid\Leftrightarrow\mid{x}+{iy}−{i}\mid=\mid{x}+{iy}−\mathrm{4}+\mathrm{3}{i}\mid \\ $$$$\Leftrightarrow\mid{x}+{i}\left({y}−\mathrm{1}\right)\mid=\mid{x}−\mathrm{4}+{i}\left({y}+\mathrm{3}\right)\mid\:\Leftrightarrow\sqrt{{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({y}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\Leftrightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{1}\:={x}^{\mathrm{2}} −\mathrm{8}{x}\:+\mathrm{16}\:+{y}^{\mathrm{2}} +\mathrm{6}{y}\:+\mathrm{9}\:\Leftrightarrow \\ $$$$−\mathrm{2}{y}+\mathrm{1}\:=−\mathrm{8}{x}\:+\mathrm{6}{y}\:+\mathrm{25}\:\Leftrightarrow−\mathrm{2}{y}+\mathrm{1}+\mathrm{8}{x}−\mathrm{6}{y}−\mathrm{25}\:=\mathrm{0}\:\Leftrightarrow \\ $$$$\mathrm{8}{x}−\mathrm{8}{y}−\mathrm{24}\:=\mathrm{0}\:\Leftrightarrow{x}−{y}−\mathrm{3}\:=\mathrm{0}\:\:\:{so}\:{the}\:{locus}\:{is}\:{a}\:{line}. \\ $$

Answered by mr W last updated on 17/Aug/19

∣z − i∣ = ∣z − 4 +3 i∣ means the distance from the variable point P(x,y) to the point A(0,1) is equal to the distance from P to the point B(4,−3). the locus of point P is therefore the perpendicular bisector of AB, i.e. the locus is a line. z=x+yi ∣z−i∣=(√(x^2 +(y−1)^2 )) ∣z−4+3i∣=(√((x−4)^2 +(y+3)^2 )) ⇒x^2 +(y−1)^2 =(x−4)^2 +(y+3)^2 ⇒y=x−3 ← eqn. of locus

$$\mid{z}\:−\:\mathrm{i}\mid\:=\:\mid{z}\:−\:\mathrm{4}\:+\mathrm{3}\:\mathrm{i}\mid\:{means} \\ $$$${the}\:{distance}\:{from}\:{the}\:{variable}\:{point} \\ $$$${P}\left({x},{y}\right)\:{to}\:{the}\:{point}\:{A}\left(\mathrm{0},\mathrm{1}\right)\:{is}\:{equal} \\ $$$${to}\:{the}\:{distance}\:{from}\:{P}\:\:{to}\:{the}\:{point} \\ $$$${B}\left(\mathrm{4},−\mathrm{3}\right).\:{the}\:{locus}\:{of}\:{point}\:{P}\:{is} \\ $$$${therefore}\:{the}\:{perpendicular}\:{bisector} \\ $$$${of}\:{AB},\:{i}.{e}.\:{the}\:{locus}\:{is}\:{a}\:{line}. \\ $$$${z}={x}+{yi} \\ $$$$\mid{z}−{i}\mid=\sqrt{{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mid{z}−\mathrm{4}+\mathrm{3}{i}\mid=\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({y}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({y}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{y}={x}−\mathrm{3}\:\leftarrow\:{eqn}.\:{of}\:{locus} \\ $$

Commented by Rio Michael last updated on 17/Aug/19

thanks so much sir

$${thanks}\:{so}\:{much}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com